CSP-S 模拟60
已经连续好几次挂掉了

T1 嘟嘟噜
约瑟夫问题,到着往前推编号 (x+m)%i ,然而n是1e9的,而且会发现m 1e5小于n,所以会有很多不用取模的时候,直接跳过就可以了
具体的 设现在编号为now ,该第i轮了,求 now+x*m>i+x ,O(1)求当前可以直接跳的轮数跳过去(考试时想到了这么跳,没有想到柿子)
叉乘 $ \sum\limits_{1<=i<j<=n} (x_i*y_j-y_i*x_j)^2 $ ,简单拆一下式子:$ x_i^2y_j^2+y_i^2x_j^2-2x_iy_ix_jy_j $
如果去掉i<j的限制,可以发现 $ \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n}x_i^2x_j^2+y_i^2x_j^2-2x_iy_ix_jy_j $
继续化简$ 2*\sum\limits x^2*\sum\limits y^2-2*(\sum\limits xy)^2 $
发现这里面包含了点对(i,j),(j,i),而我们只要(i,j)且这两个叉乘是一样的,所以直接除以2,就是答案,至于叉乘(i,i)等于0,对答案无影响
最终答案就是 $ \sum\limits_{i=L}^{R} x^2*\sum\limits_{i=L}^{R} y^2-(\sum\limits_{i=L}^{R} xy)^2 $
三个树状数组维护
T3 凤凰院凶真
n^2 dp f[i][j] 当a[i]==b[j] 表示,a[i],b[j]对应时的最长公共子序列长度 ,以下粘上题解
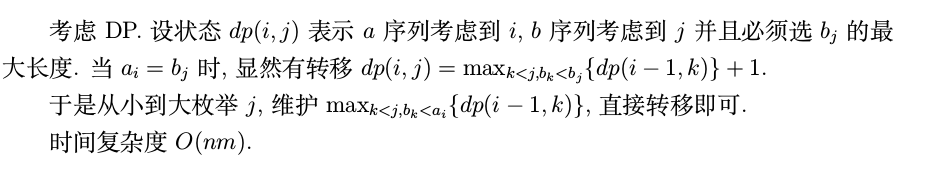




 浙公网安备 33010602011771号
浙公网安备 33010602011771号