20190730 NOIP模拟测试10「辣鸡·模板·大佬」

说实话，真心不想写，考得太差了，35分，rank34/55

不过反思、题解还是要写的

考试的时候看见T2 「 模板 」，绝对没那么简单，直接跳，先做的T1，花了两个小时，又花了一个多小时搞T3，T2就这样丢了，结果T3爆零，自我感觉能AC的T1只拿了35

总结几点：

1.永远不要寄希望于某一道题，更不要死磕

2.把握时间分配，如Deepinc所说，先评估难度，大概半小时左右把最简单的搞出来，在去想难一点儿的，半个小时还没有思路就有啥思路打啥

3.期望放低，失望的概率会小，在博客里疯狂踩自己可以拿Rank1 QWQ

T1 辣鸡

　　n^2大暴搜，一个（x*y）的块里面有(x-1)*(y-1) 个氢键，再讨论块与块之间的氢键数量，接触的部分的块的个数d，为（d-1）*2，如果除了接触的部分，有一端出头数量+1，

有两端出头则+2

　　Ps: 做题时考虑仔细，不要漏掉任何情况

　　Pss：一定按照题中给出的坐标系的形式建图，比如此题x是横坐标，y是纵坐标，不要像我一样把坐标系翻转，按y排序导致被卡

 

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define ll long long
int n;
struct node{
    ll u,l,d,r;
}q[110000];
inline int cmp(node a,node b){
    return a.l<b.l;
}
long long ans;
int main(){
    scanf("%d",&n);
    for(register int i=1;i<=n;i++){
        scanf("%lld%lld%lld%lld",&q[i].l,&q[i].d,&q[i].r,&q[i].u);
        ans+=(ll)(q[i].u-q[i].d)*(q[i].r-q[i].l)*2;
    }
    //cout<<ans<<endl;
    sort(q+1,q+n+1,cmp);
    for(register int i=1;i<n;i++){
        for(register int j=i+1;j<=n&&q[i].r+1>=q[j].l;j++){
            int minn;
        //    cout<<i<<" "<<j<<endl;
            if(q[j].l==q[i].l){
                if(q[j].u+1==q[i].d||q[j].d-1==q[i].u){
                    minn=min(q[i].r-q[i].l+1,q[j].r-q[j].l+1);
                    ans+=(minn-1)*2;
                    if(q[j].r!=q[i].r) ans++;
                }
            }
            else if(q[j].l<=q[i].r){
                if(q[j].u+1==q[i].d||q[j].d-1==q[i].u){
                    if(q[j].r>q[i].r) minn=q[i].r-q[j].l+1;
                    else if(q[j].r<q[i].r) minn=q[j].r-q[j].l+1;
                    else minn=q[i].r-q[j].l+1;
                    ans+=(minn-1)*2;
                    ans+=(q[j].r==q[i].r)?1:2;
                }
            }
            else if(q[i].r+1==q[j].l){
                if(q[j].u==q[i].d-1||q[j].d==q[i].u+1) ans++;
                else if(q[j].u<q[i].u&&q[j].u>=q[i].d){
                    if(q[j].d>q[i].d) minn=q[j].u-q[j].d+1;
                    else if(q[j].d<q[i].d) minn=q[j].u-q[i].d+1;
                    else if(q[j].d==q[i].d) minn=q[j].u-q[i].d+1;
                    ans+=(minn-1)*2;
                    ans+=(q[j].d==q[i].d)?1:2;
                }
                else if(q[j].u>q[i].u&&q[i].u>=q[j].d){
                    if(q[j].d>q[i].d) minn=q[i].u-q[j].d+1;
                    else if(q[j].d<q[i].d) minn=q[i].u-q[i].d+1;
                    else if(q[j].d==q[i].d) minn=q[i].u-q[j].d+1;
                    ans+=(minn-1)*2;
                    ans+=(q[j].d==q[i].d)?1:2;  
                }
                else if(q[j].u==q[i].u){
                    if(q[j].d>q[i].d) minn=q[i].u-q[j].d+1;
                    else if(q[j].d<q[i].d) minn=q[i].u-q[i].d+1;
                    else minn=q[i].u-q[i].d+1;
                    ans+=(minn-1)*2;
                    ans+=(q[j].d==q[i].d)?0:1;
                }
            }
        }
    }
    printf("%lld\n",ans);
}

T2 模板

　　线段树维护区间球的个数，颜色的个数，查询时查询球数是该点桶的数量的区间（从1～？）的颜色数

　　颜色要离散化，因为有负数而且颜色值可能会很大

　　线段树用启发式合并，即保留最大子树的信息，加上其他子树更新当前节点的信息

　　PS：注意询问函数的答案统计和递归边界，否则会死循环

　　PS：注意每次处理完一个节点且这个节点信息不保留，清零最好用时间戳（也就是f懒标记）清空，一定不能用memset　　　

#include<iostream>
#include<cstdio>
#include<vector>
#include<cstring>
#include<algorithm>
#include<map>
using namespace std;
int n,m,Q,num,cet,root;
const int maxn=1e5+100;
int ls[410000],rs[410000],f[410000],qiunum[410000],colornum[410000],w[maxn],size[maxn],ma[maxn],is_here[maxn],loc[maxn],wolan[maxn],key[maxn];
vector<int>son[110000],point[110000];
int tmp[maxn],ans[maxn];
inline void down(int t){
    qiunum[ls[t]]=colornum[ls[t]]=0;
    qiunum[rs[t]]=colornum[rs[t]]=0;
    f[ls[t]]=f[rs[t]]=1;
    if(ls[ls[t]]==0&&rs[ls[t]]==0) f[ls[t]]=0;
    if(ls[rs[t]]==0&&rs[rs[t]]==0) f[rs[t]]=0;
    f[t]=0;
}
inline void build(int  &t,int l,int r){
    if(!t) t=++cet;
     if(l==r) return ;
    int mid=(l+r)/2;
    build(ls[t],l,mid);
    build(rs[t],mid+1,r);
}
inline void dfs1(int x,int pre){
    size[x]=1+point[x].size();
    int mxn=0;
    for(register int i=0;i<son[x].size();i++){
        int y=son[x][i];
        if(y==pre) continue;
        dfs1(y,x);
        size[x]+=size[y];
        if(size[y]>mxn) ma[x]=y,mxn=size[y];
    }
}
inline void change(int t,int l,int r,int x){
    if(l==r){
        colornum[t]=0;
        return;
    }
    if(f[t]) down(t);
    int mid=(l+r)/2;
    if(mid>=x) change(ls[t],l,mid,x);
    else change(rs[t],mid+1,r,x);
    qiunum[t]=qiunum[ls[t]]+qiunum[rs[t]];
    colornum[t]=colornum[ls[t]]+colornum[rs[t]];
}
int landenum;
inline void add(int t,int l,int r,int x,int k){
    if(l==r){
        qiunum[t]+=k;
        colornum[t]+=k;
        if(wolan[w[l]]!=landenum) wolan[w[l]]=0,is_here[w[l]]=0,loc[w[l]]=0;
        if(k==1&&!is_here[w[l]]) is_here[w[l]]=1,loc[w[l]]=l,wolan[w[l]]=landenum;
        else if(k==1&&is_here[w[l]]){
            if(loc[w[l]]<l)  colornum[t]=0;
            else{
                change(1,1,m,loc[w[l]]);
                loc[w[l]]=l;
            }
        }
        return;
    }
    if(f[t]) down(t);
    int mid=(l+r)/2;
    if(mid>=x) add(ls[t],l,mid,x,k);
    else add(rs[t],mid+1,r,x,k);
    qiunum[t]=qiunum[ls[t]]+qiunum[rs[t]];
    colornum[t]=colornum[ls[t]]+colornum[rs[t]];
}
inline void go_add(int x,int pre,int k){
    for(register int i=0;i<point[x].size();i++)
        add(1,1,m,point[x][i],k);
    for(register int i=0;i<son[x].size();i++)
         if(son[x][i]!=pre)
              go_add(son[x][i],x,k);
}
inline int ask(int t,int x){
    if(x==0) return 0;
    if(qiunum[t]==0) return 0;
    if(t==0) return 0;
    if(qiunum[t]<x) return colornum[t];
    if(qiunum[t]==x) return colornum[t];
    if(qiunum[ls[t]]==x) return colornum[ls[t]];
    else if(qiunum[ls[t]]>x) return ask(ls[t],x);
    return colornum[ls[t]]+ask(rs[t],x-qiunum[ls[t]]);
}
inline void dfs(int x,int keep,int pre){
    landenum++;
    for(register int i=0;i<son[x].size();i++){
        int y=son[x][i];
        if(y==pre||y==ma[x]) continue;
        dfs(y,0,x);
    }
    if(ma[x]) dfs(ma[x],1,x);
    for(register int i=0;i<point[x].size();i++)
        add(1,1,m,point[x][i],1);
    for(register int i=0;i<son[x].size();i++){
        int y=son[x][i];
        if(y==pre||y==ma[x]) continue;
        go_add(son[x][i],x,1);
    }
    ans[x]=ask(1,tmp[x]);
    if(!keep){
        f[1]=1,qiunum[1]=0,colornum[1]=0;
    }
}
int main(){
    scanf("%d",&n);
    int  x,y;
    for(register int i=1;i<n;i++){
        scanf("%d%d",&x,&y);
        son[x].push_back(y);
        son[y].push_back(x);
    }
    for(register int i=1;i<=n;i++)
        scanf("%d",&tmp[i]);
    scanf("%d",&m);
    build(root,1,m);
    for(register int i=1;i<=m;i++){
        scanf("%d%d",&x,&y);
        w[i]=key[i]=y;
        point[x].push_back(i);
    }
    cout<<endl;
    sort(key+1,key+m+1);
    int q=unique(key+1,key+m+1)-key- 1;
    for(register int i=1;i<=m;i++){
        w[i]=lower_bound(key+1,key+q+1,w[i])-key;
    }
    dfs1(1,0);
    dfs(1,0,0);
    scanf("%d",&Q);
    while(Q--){
        scanf("%d",&x);
        printf("%d\n",ans[x]);
    }
    return 0;
}

T3 大佬

　　有一个完全组合数学的思路，对于n道题的难度，方案数是n^m，而这每一种方案对应一种第一天……，第二天……，第三天……的情况

　　所以每天的方案是一样的，概率也一样，n天的期望就是一天的期望乘上n天

　　另一种理解，额～就叫他加法结合律吧

                                                           

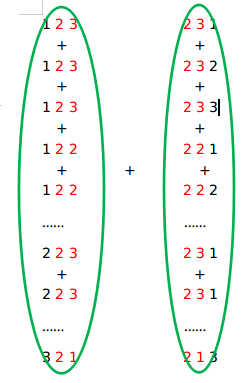
　　直观上看起来二者是相等的

　　所以n天的期望等于一天期望乘上n天

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define ll long long
const int mod=1e9+7;
int n,m,k;
ll wt[650],f[2][450],sum;
ll pow(ll a,ll b){
    ll ans=1;
    a%=mod;
    while(b){
        if(b&1) ans=ans*a%mod;
        b>>=1;
        a=a*a%mod;
    }
    return ans%mod;
}
int main(){
    scanf("%d%d%d",&n,&m,&k);
    if(k>n){
        puts("0");
        return 0;
    }
    for(int i=1;i<=m;i++){
        scanf("%lld",&wt[i]);
         if(i!=1) wt[i]=wt[i]%mod*(pow(i,k)-pow(i-1,k)+mod)%mod;
        sum=(sum+wt[i])%mod;
    }
    ll ans=pow(pow(m,k),mod-2)%mod;
    printf("%lld\n",sum*(n-k+1)%mod*ans%mod);
}