「天使玩偶」· 题解 （点分治）

仍然是我自己的做法（不要走，这可是我目前见过的时间最快的了，只有17150ms）

一开始没仔细看题我想成了所谓翻转坐标系是因为坐标有正有负，整了一堆没用的（这句话好像在哪儿听过～）

然后发现x,y均为非负整数，然后就按照学长讲的思路翻转坐标系求四遍CDQ，但是我打出了一遍CDQ的方法（虽说里边算是夹了两个）

对于一个点(x,y)来说

1. 左上有一个天使玩偶(x1,y1)， 距离为 (x-x1)+(y1-y)

2. 左下有一个天使玩偶(x1,y1)， 距离为(x-x1)+(y-y1)

3. 右上有一个天使玩偶(x1,y1)， 距离为(x1-x)+(y1-y)

4. 右下有一个天使玩偶(x1,y1)， 距离为(x1-x)+(y-y1)

没有错吧，那么接下来把式子变一变

1. 左上  (x-y)-(x1-y1)

2.左下   (x+y)-(x1+y1)

3.右上   -(x+y)+(x1+y1)    <=>  -(x+y) - (-(x1+y1))

4.右下   (y-x) -(y1-x1)

就酱紫 我们会发现 后面的 关于x1,y1的式子越大，距离越小，我们可以开 4个树状数组+4个CDQ，干他

但是那太暴力了，要优雅

 当我们用CDQ的时候，是将时间排序，然后把 x归并排序，然后只是把y存进树状数组中查询，对于y并没有实际的单调，而时间全都已经排好了不去想他，所以考虑x

可以自己手 %一下，会发现，同在左的左上和左下在CDQ的时候，都是把x小于待查询的点的x值的点的y插入树状数组里（额，有点儿绕），也就是都进行这种操作

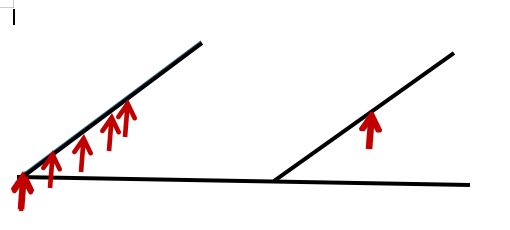
那么可以把这两个CDQ合成一个，右上右下同理，按x升序排列一遍，再按x降序排列一遍，共两遍CDQ，开两个树状使用两遍，

继续考虑，还是这个图，把它翻转一下，方便理解我加上了L,R（表示上图中升序排列的L，R）

 

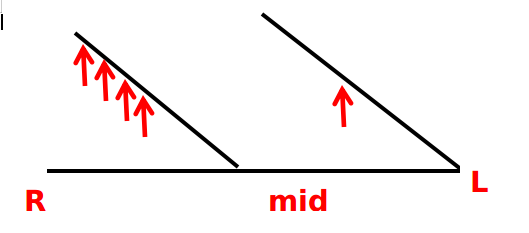
　　那么到这里，就可以想明白了，一个CDQ里夹两个那样的for循环，一遍i=L,j=mid,升序遍历并排序（用一个tmp记录），一遍i=mid,j=r,反向降序遍历，同时在这两遍遍历中用两个树状数组分别维护上和下的最大值。

　　而我们在找y的时候，左上右上是找大于待查询点y值的y中的最大值，这里我用了一个把树状数组反着用的操作。

　　原来普通的是插入时从x到末尾，查询从x到1，现在我插入时从x到1，查询从x到末尾（当然是对于上的操作，下还是一般的树状数组）

　　提醒一点，树状数组中存的数可能一定有负数，所以一开始要把树状数组置为-0x3fffffff,同时清空的时候也要这么做

　　总结一下，我们只需要走一遍CDQ用一个序列跑两遍循环，加上两个树状数组记录即可得到答案，甚至因为时间是递增的，时间那一维不需要排序，连cmp，sort都不用打，远优于排序，排序，排序再4遍CDQ的做法

　　PS：对于for循环以及清空等操作，建议自己一个个打，不要复制粘贴，Lockey就是因为粘了却忘记改细节，卡了一下午……

　　感觉写的好的话，麻烦顶一下，谢谢关照！

　　上代码（关键处有解释）

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int n,m,num,tot,ans[1100000],maxy;
int tr1[1100000],tr2[1100000];
struct node{
    int id,x,y;
    int cnt;
}q[1100000],tmp[1100000];
int cmp(node a,node b){
    return a.id==b.id?((a.x==b.x)?(a.y<b.y):(a.x<b.x)):a.id<b.id;
}
int lowbit(int x){
    return x&(-x);
}
void add1(int x,int k){
    while(x){
        tr1[x]=max(tr1[x],k);
        x-=lowbit(x);
    }
}
void add2(int x,int k){
    while(x<=maxy){
        tr2[x]=max(tr2[x],k);
        x+=lowbit(x);
    }
}
int ask1(int x){
    int ans=-0x3ffffff;
    while(x<=maxy){
        ans=max(tr1[x],ans);
        x+=lowbit(x);
    }
    return ans;
}
int ask2(int x){
    int ans=-0x3fffffff;
    while(x){
        ans=max(tr2[x],ans);
        x-=lowbit(x);
    }
    return ans;
}
void clear1(int x){
    while(x){
        tr1[x]=-0x3fffffff;
        x-=lowbit(x);
    }
}
void clear2(int x){
    while(x<=maxy){
        tr2[x]=-0x3fffffff;
        x+=lowbit(x);
    }
}
void CDQ(int l,int r){
    if(l==r) return;
    int mid=(l+r)/2,i=l,j=mid+1,p=l;
    CDQ(l,mid),CDQ(mid+1,r);
    while(i<=mid&&j<=r){
        if(q[i].x<=q[j].x){
            if(q[i].cnt==1){
                add1(q[i].y,q[i].x-q[i].y);//距离为 (x0-y0)-(x1-y1)，找左上(x1-y1) 最大值
                add2(q[i].y,q[i].x+q[i].y);//距离为 (x0+y0)-(x1+y1)，找左下(x1+y1) 最大值
            }
            tmp[p++]=q[i++];
        }
        else{
            if(q[j].cnt==2){
                ans[q[j].id]=min(ans[q[j].id],(q[j].x-q[j].y)-ask1(q[j].y));//同上
                ans[q[j].id]=min(ans[q[j].id],(q[j].x+q[j].y)-ask2(q[j].y));//同上
            }
            tmp[p++]=q[j++];
        }
    }
    while(i<=mid){//全跑光
        if(q[i].cnt==1){
             add1(q[i].y,q[i].x-q[i].y);
             add2(q[i].y,q[i].x+q[i].y);
        }
        tmp[p++]=q[i++];
    }
    while(j<=r){//同上
        if(q[j].cnt==2){
            ans[q[j].id]=min(ans[q[j].id],(q[j].x-q[j].y)-ask1(q[j].y));//同上
            ans[q[j].id]=min(ans[q[j].id],(q[j].x+q[j].y)-ask2(q[j].y));//同上
        }
        tmp[p++]=q[j++];
    }
    for(int k=l;k<=mid;k++){//消除影响
        if(q[k].cnt==1){
            clear1(q[k].y);
            clear2(q[k].y);
        }
    } 
    //跑右边的   
    i=mid,j=r;
    while(i>=l&&j>=mid+1){
        if(q[i].x>=q[j].x){
            if(q[i].cnt==1){
                add1(q[i].y,-(q[i].x+q[i].y)); //距离为 -(x+y)-(-(x1+y1)) 维护右上 -(x1+y1) 最大值
                add2(q[i].y,q[i].y-q[i].x); //距离为 (y-x)-(y1-x1) 维护右下 （y1-x1） 最大值
            }
            i--;
        }
        else{
            if(q[j].cnt==2){
                ans[q[j].id]=min(ans[q[j].id],-(q[j].x+q[j].y)-ask1(q[j].y));
                ans[q[j].id]=min(ans[q[j].id],(q[j].y-q[j].x)-ask2(q[j].y));
            }
            j--;
        }
    }
    while(i>=l){//全跑光
        if(q[i].cnt==1){
            add1(q[i].y,-(q[i].x+q[i].y));
            add2(q[i].y,q[i].y-q[i].x); 
        }
        i--;
    }
    while(j>=mid+1){//同上
        if(q[j].cnt==2){
            ans[q[j].id]=min(ans[q[j].id],-(q[j].x+q[j].y)-ask1(q[j].y));
            ans[q[j].id]=min(ans[q[j].id],(q[j].y-q[j].x)-ask2(q[j].y));
        }
        j--;
    }
    for(int k=l;k<=mid;k++){//消除影响
        if(q[k].cnt==1){
            clear1(q[k].y);
            clear2(q[k].y);
        }
    }
    for(int k=l;k<=r;k++) q[k]=tmp[k];
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        ++num;
        scanf("%d%d",&q[num].x,&q[num].y);
        maxy=max(maxy,q[num].y);
        q[num].id=tot;
        q[num].cnt=1;
    }
    for(int i=1;i<=m;i++){
        ++num;
        scanf("%d%d%d",&q[num].cnt,&q[num].x,&q[num].y);
        maxy=max(maxy,q[num].y);
        if(q[num].cnt==2)q[num].id=++tot;
    }
    for(int i=0;i<=tot;i++) ans[i]=0x3ffffff;
    for(int i=1;i<=maxy;i++) tr1[i]=tr2[i]=-0x3fffffff;
    CDQ(1,num);
    for(int i=1;i<=tot;i++){
        printf("%d\n",ans[i]);
    }
}