[POJ2942]Knights of the Round Table(点双+二分图判定——染色法)

建补图，是两个不仇恨的骑士连边，如果有环，则可以凑成一桌和谐的打麻将

不能直接缩点，因为直接缩点求的是连通分量，点双缩点只是把环缩起来

普通缩点                                                                                               点双缩点

　　

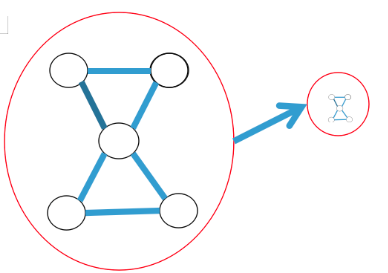
由图可知，左图中的缩法不符题意，而右图两个缩完后的点都满足题意

然后题中说必须要奇数个骑士参加会议，即找奇圈（有奇数个点的圈）

问题就转化成缩点后判断一个点是否在奇圈里，这就用到了点双的性质

点双连通分量有两个性质：1.如果该分量里有一个奇圈，那么其他所有点也必然在某个奇圈中；2.含有一个奇圈的充要条件是该分量不是二分图。

所以我们只需要缩完点之后枚举V-DCC判断是不是二分图，不是二分图就是奇圈

那么判断二分图用染色法判断即可

注意一个骑士不可以参加会议

这句话是自言自语： Lockey注意要检查变量名是否写对了

二分图定义：

　　一个无向图，使得顶点集V可以分割为两个互不相交的子集A,B，使得所有边两端分别属于两个子集A,B。

度娘解释

 

　　二分图是这样一个图： 有两顶点集且图中每条边的的两个顶点分别位于两个顶点集中，每个顶点集中没有边直接相连接！

 

　　无向图G为二分图的充分必要条件是，G至少有两个顶点,且其所有回路的长度均为偶数。

 

　　判断二分图的常见方法是染色法： 开始对任意一未染色的顶点染色，之后判断其相邻的顶点中，若未染色则将其染上和相邻顶点不同的颜色， 若已经染色且颜色和相邻顶点的颜　色相同则说明不是二分图，若颜色不同则继续判断，bfs和dfs可以搞定！

　　易知：任何无回路的的图均是二分图

　　

#include<iostream>
#include<cstdio>
#include<vector>
#include<cstring>
using namespace std;
int n,m,a[1100][1100],dfn[1100],low[1100],st[1100],ins[1100],num,v[1100],cnt,sp[1100],ok[1100],flag[1100],root;
vector<int>son[1100],spn[1100];
void tarjan(int x,int pre){
    dfn[x]=low[x]=++num;
    if(x==root&&son[x].size()==0) spn[++cnt].push_back(x);
    st[++st[0]]=x;
    ins[x]=1;
    for(int i=0;i<son[x].size();i++){
        int y=son[x][i];
        if(y==pre) continue;
        if(!dfn[y]){
            tarjan(y,x);
            low[x]=min(low[x],low[y]);
            if(low[y]>=dfn[x]){
                cnt++;
                int w;
                do{
                    w=st[st[0]--];
                    ins[w]=0;
                    spn[cnt].push_back(w);
                }while(w!=y);
                spn[cnt].push_back(x);
            }
        }
        else low[x]=min(low[x],dfn[y]);
    }
}
int dfs(int x,int pre,int loc){//是二分图返回0,是奇圈返回1
    v[x]=v[pre]^1;
    //cout<<x<<" "<<v[x]<<endl;
    for(int i=0;i<son[x].size();i++){
        int y=son[x][i];
        //cout<<y<<" "<<" "<<flag[y]<<" "<<v[y]<<endl;
        if(!flag[y]||y==pre) continue;
        if(v[y]==-1){
            if(dfs(y,x,loc)) return 1;
        }
        else if(v[y]==v[x]) return 1;
    }
    return 0;
}

int main(){
    scanf("%d%d",&n,&m);
    while(n!=0||m!=0){
        int x,y;
        for(int i=1;i<=m;i++){
            scanf("%d%d",&x,&y);
            a[x][y]=a[y][x]=1;
        }
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                if(a[i][j]||i==j) continue;
                son[i].push_back(j);
            }
        }
        for(int i=1;i<=n;i++){
            if(!dfn[i]) root=i,tarjan(i,0);
        }
        memset(v,-1,sizeof(v));
        v[0]=0;
        //cout<<cnt<<endl;
        for(int i=1;i<=cnt;i++){
            if(spn[i].size()==1) continue;
            for(int j=0;j<spn[i].size();j++) flag[spn[i][j]]=1;
            if(dfs(spn[i][0],0,i))
                for(int j=0;j<spn[i].size();j++)    
                    ok[spn[i][j]]=1;
            for(int j=0;j<spn[i].size();j++) flag[spn[i][j]]=0,v[spn[i][j]]=-1;
        }
        int ans=0;
        for(int i=1;i<=n;i++) ans+=ok[i];
        printf("%d\n",n-ans); 
        for(int i=1;i<=n;i++){
            dfn[i]=low[i]=0;
            st[i]=0;
            ins[i]=0;
            ok[i]=0;
            sp[i]=0;
            son[i].clear();
            spn[i].clear();
        }
        st[0]=0;
        memset(v,-1,sizeof(v));
        memset(a,0,sizeof(a));
        num=cnt=0;
        scanf("%d%d",&n,&m);
    }
    
}