CS61B sp2018笔记 | Lists
Lists
1. IntLists
下面我们来一步一步的实现List类,首先你可以实现一个最简单的版本:
public class IntList {
public int first;
public IntList rest;
public IntList(int f, IntList r) {
first = f;
rest = r;
}
}
这样一个链表看起来特别丑陋,比如,我们要生成一个拥有5,10,15三个整数的链表,不得不这么做:
IntList L = new IntList(5, null);
L.rest = new IntList(10, null);
L.rest.rest = new IntList(15, null);
或者时这样:
IntList L = new IntList(15, null);
L = new IntList(10, L);
L = new IntList(5, L);
尽管看起来丑陋,使用起来也十分困难,不过我们还是要为它添加几个方法,首先是size方法:
/** Return the size of the list using... recursion! */
public int size() {
if (rest == null) {
return 1;
}
return 1 + this.rest.size();
}
/** Return the size of the list using no recursion! */
public int iterativeSize() {
IntList p = this;
int totalSize = 0;
while (p != null) {
totalSize += 1;
p = p.rest;
}
return totalSize;
}
随后的几个方法在Lab 2(Lab 2同时教了debug)中呈现,先是讲解方法分为Destructive和Non-Destructive,也就是是否改变参数的值。然后讲义部分给出了将一个链表所有数值平方的三种实现,分别使用了Destructive版本、Non-Destructive迭代版本和Non-Destructive递归版本(实现代码),然后让学生自己实现链表拼接的Destructive版本和Non-Destructive版本,下面是我的实现:
/**
* Returns a list consisting of the elements of A followed by the
* * elements of B. May modify items of A. Don't use 'new'.
*/
public static IntList dcatenate(IntList A, IntList B) {
//TODO: fill in method
IntList res = A;
while (A.rest != null) {
A = A.rest;
}
A.rest = B;
return res;
}
/**
* Returns a list consisting of the elements of A followed by the
* * elements of B. May NOT modify items of A. Use 'new'.
*/
public static IntList catenate(IntList A, IntList B) {
//TODO: fill in method
IntList res = new IntList(A.first, null);
IntList ptr = res;
A = A.rest;
while (A != null) {
ptr.rest = new IntList(A.first, null);
ptr = ptr.rest;
A = A.rest;
}
ptr.rest = B;
return res;
}
2. SLLists
理论上讲,IntList可以实现一个链表能够做的所有事,不过它难以使用,代码难以理解。最主要的是,如果一个程序员想使用它,就必须了解它复杂的递归思想,要手动写出next的指向,这会大大降低这种数据结构的使用率。
所以,在原有IntList的基础上,我们设计一种新的类SLLists(Single Linked Lists),并为它提供一系列的方法。
首先我们创建一个新的类IntNode:
public class IntNode {
public int item;
public IntNode next;
public IntNode(int i, IntNode n) {
item = i;
next = n;
}
}
除了名字不同以外,它好像和IntList没有任何区别,没错,我们还需要创建另外一个类SLList:
public class SLList {
public IntNode first;
public SLList(int x) {
first = new IntNode(x, null);
}
}
它将IntNode进行了封装,会使用者提供了更简洁的使用方法,当使用IntList和SLList时,你可以清楚的看出SLList优秀的地方:
IntList L1 = new IntList(5, null);
SLList L2 = new SLList(5);
SLList隐藏了IntNode中靠next取得的联系,使用者不必关心SLList内部如何实现,只知道如何用它来存储数据就足够了。我们再为SLList添加几个方法:
public class SLList {
public IntNode first;
public SLList(int x) {
first = new IntNode(x, null);
}
/** Adds an item to the front of the list. */
public void addFirst(int x) {
first = new IntNode(x, first);
}
/** Retrieves the front item from the list. */
public int getFirst() {
return first.item;
}
}
通过比较,你会发现SLList使用起来更简单了:
SLList L = new SLList(15);
L.addFirst(10);
L.addFirst(5);
int x = L.getFirst();
IntList L = new IntList(15, null);
L = new IntList(10, L);
L = new IntList(5, L);
int x = L.first;
再来比较一下它们的内部实现:
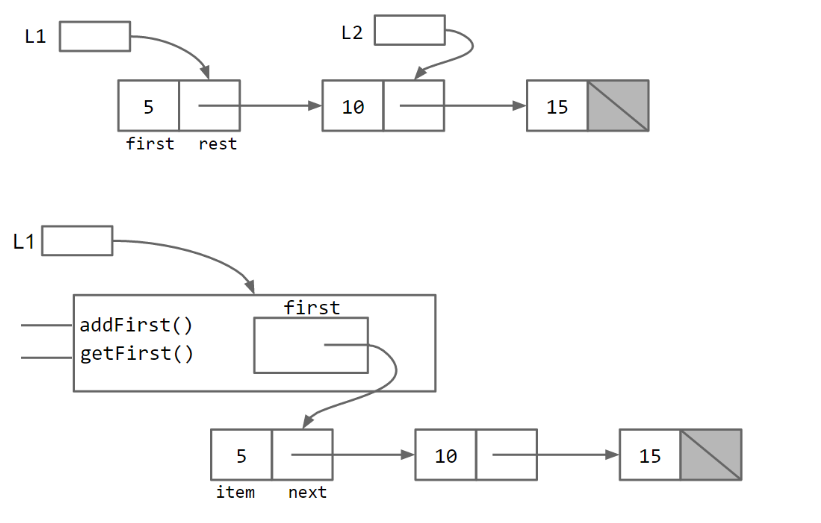
不过,如果使用者这样使用呢?
SLList L = new SLList(15);
L.addFirst(10);
L.first.next.next = L.first.next;

这将会导致死循环,所以我们要把first声明为私有变量,禁止使用者调用它,这样,上面的操作将会报错。不过这时,我们有两个.java文件,使用者每次使用都要导入这两个文件,所以,我们可以将IntNode写入SLList类中,这也称为Nested Classes。并且IntNode不会调用它以外的SLList中的值,所以我们把它声明为static类型,实现如下:
public class SLList {
public static class IntNode {
public int item;
public IntNode next;
public IntNode(int i, IntNode n) {
item = i;
next = n;
}
}
private IntNode first;
...
我们再为它添加size方法:
/** Returns the size of the list starting at IntNode p. */
private static int size(IntNode p) {
if (p.next == null) {
return 1;
}
return 1 + size(p.next);
}
public int size() {
return size(first);
}
然而,size方法内部使用了递归或者迭代,如果长度为1000的链表的size需要耗时2秒,那么计算长度为1,000,000的链表的size就可能会耗时2000秒。所以我们要将size方法的时间复杂度设计为常数,这里用到了储存(caching)的思想,我们添加一个size变量,并时刻跟踪改变它的值:
public class SLList {
... /* IntNode declaration omitted. */
private IntNode first;
private int size;
public SLList(int x) {
first = new IntNode(x, null);
size = 1;
}
public void addFirst(int x) {
first = new IntNode(x, first);
size += 1;
}
public int size() {
return size;
}
...
}
这样,无论链表多么长,size方法都会很快的返回它的值。下面我们再仔细思考,如果一个链表为空,我们如何表示它?一种方法是为它设计空参构造函数:
public SLList() {
first = null;
size = 0;
}
不过它的addLst方法将变得很庞大,而且之后每添加一个类似的方法,我们都需要考虑链表为空的情况。
public void addLast(int x) {
size += 1;
if (first == null) {
first = new IntNode(x, null);
return;
}
IntNode p = first;
while (p.next != null) {
p = p.next;
}
p.next = new IntNode(x, null);
}
所以,在设计伊始,我们设计的模型要在根本上解决这个问题。这里的设计思想一开始可能会难以接受,不过渐渐你会发现它的优秀之处。我们采取的手段是添加一个空的node节点,称之为sentinel node。
于是,当我们通过SLList L = new SLList()实例化一个SLList对象时,它的内部将会变成这样:
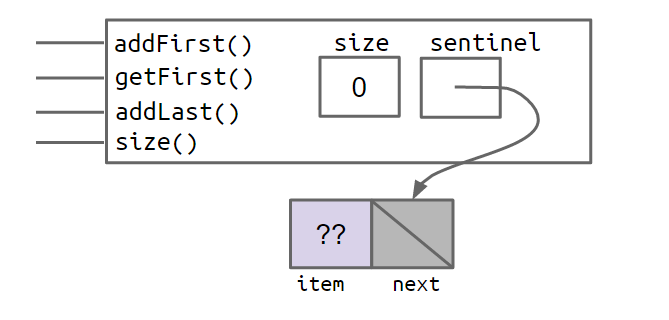
当为链表添加5,10,15三个元素时,它将变成这样:

这样,addLast方法就变得简洁易读多了。
public void addLast(int x) {
size += 1;
IntNode p = sentinel;
while (p.next != null) {
p = p.next;
}
p.next = new IntNode(x, null);
}
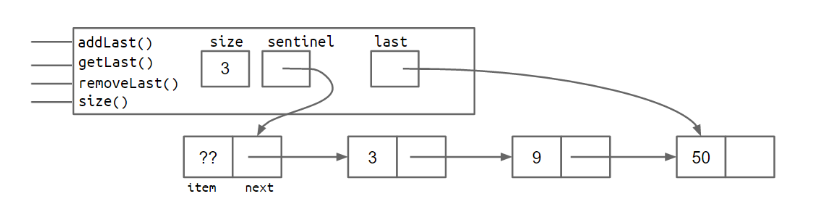
但是,addLst方法同样存在一个问题,就是链表的长度越长,它的执行时间也就越长。为了解决这一问题,我们同样可以使用储存的思想,为它添加一个last变量,时刻记录尾节点的位置。
public class SLList {
private IntNode sentinel;
private IntNode last;
private int size;
public void addLast(int x) {
last.next = new IntNode(x, null);
last = last.next;
size += 1;
}
...
}
它的内部就变成了下面这样:
再考虑,如果我们要添加一个移除最后一个元素的removeLast方法,该如何实现?大致的思路就是获取到倒数第二个节点,然后将倒数第二个节点的next设为null,可是,如何获取到倒数第二个节点呢?
从sentinel向后遍历是不可能的了,那将使方法具有线性复杂度,其实,在现有的模型结构下很难实现,所以,我们不得在现有模型的基础上再次设计一种新的数据结构,也就是下面的DLList。
3. DLLists
这一次的改造更加彻底,我们在每一个IntNode中添加一个prev变量,也就是为整个链表添加了Back pointers :
public class IntNode {
public IntNode prev;
public int item;
public IntNode next;
}
之所以称之为DLList,其实是Doubly linked list,也就是双向链表,空链表和非空链表的内部结构如下所示:

目前,我们设计的DLList已经可以在头部和尾部进行快速的添加、获取和删除操作,唯一不足的地方就是last指针有时指向带有数据的节点,有时指向sentinel这种特殊的空接点,在以后的实现中可能会造成混乱。
所以,我们可以用以下两种方法来避免:
-
一种是在尾部增加一个sentinel空结点。
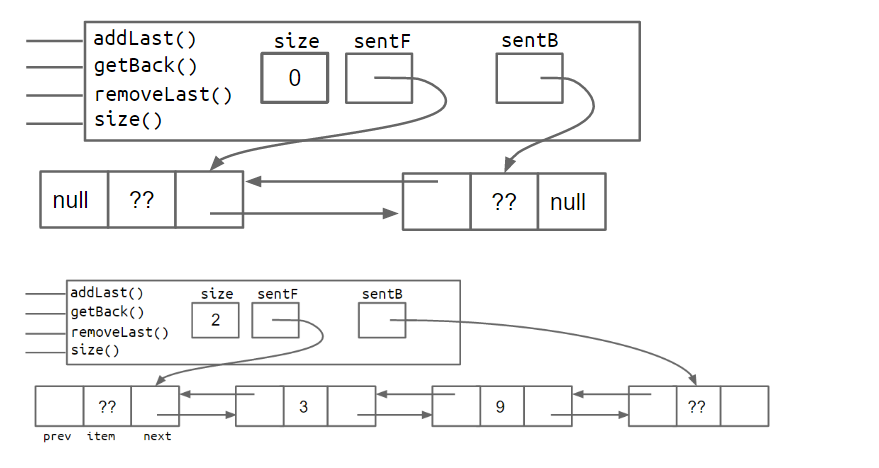
-
一种是采用
circle的的思想,让首尾指针指向同一个sentinel空结点。

这两种设计思想都很完美,在这里,cs61b让学生自己实现这种数据结构,并添加一定的方法,而且需要设计成泛型,也就是Project 1A的第一部分。
我采取的第二种实现版本,这里是我的实现,上一个目录有说明文件。
至此,我们已经设计并实现了一种健壮实用易扩展的数据结构,更重要的是在设计过程中发现问题、解决问题的设计思想。底层实现过程和设计思想,这也是cs61b最重视的部分。

