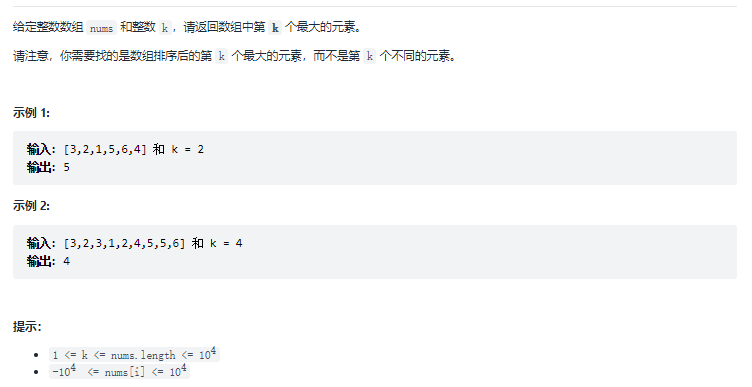
215. 数组中的第K个最大元素_中等_数组

 

 暴力，排序取值

class Solution {

    public int findKthLargest(int[] nums, int k) {
        Arrays.sort(nums);
        return nums[nums.length-k];
    }

}

优先队列

    //思路是创建一个大小为k的优先队列，对每一个元素判断和优先队列对头的元素（最小值，小顶堆）
    //进行比较，如果对头元素小，则移除加入新的元素，所以最终队列就是前k大，队头就是我们要的
    public int findKthLargest(int[] nums, int k) {
        PriorityQueue  queue = new PriorityQueue(k);
        for (int i = 0; i < nums.length; i++) {
//            System.out.println(queue.size());
            if(queue.size()<k){
                queue.add(nums[i]);
            }else{
                if(nums[i]> (int)queue.peek()){
//                    System.out.println(queue.peek());
                    queue.poll();
                    queue.add(nums[i]);
                }
            }
        }
        return (int)queue.peek();
    }

快排（每次确定一个指定大的数据，当为k时就可以返回）

 

 

class Solution {
    //用一个全局变量来记录quickSelect的结果
    private int num;

    public int findKthLargest(int[] nums, int k) {
//        quickSelect(nums,k,0,nums.length - 1);//快排选择
        int num = heapSelect(nums, k);//堆选择
        return num;
    }

    /**
     * 快排选择
     * @param nums 数组
     * @param k 第几大
     * @param left 左边界
     * @param right 右边界
     */
    public void quickSelect(int[] nums,int k,int left,int right){
        //递归终止条件
        if(left > right){
            return;
        }

        int pivot = nums[left];//基准值
        int leftIndex = left;//左指针
        int rightIndex = right;//右指针
        //用挖坑法逐步替换元素，使基准值归位
        while(leftIndex < rightIndex){
            //在右边寻找一个小于基准值的数，并与左指针所在位置交换
            while(leftIndex < rightIndex && nums[rightIndex] >= pivot){
                rightIndex--;
            }
            if(leftIndex < rightIndex){
                nums[leftIndex] = nums[rightIndex];
            }
            //在左边寻找一个大于基准值的数，并与右指针所在位置交换
            while(leftIndex < rightIndex && nums[leftIndex] < pivot){
                leftIndex++;
            }
            if(leftIndex < rightIndex){
                nums[rightIndex] = nums[leftIndex];
            }
        }
        nums[leftIndex] = pivot;//将基准值归位
        //以上都是快排的基本操作，接下来则是利用快排找出第k大的数
        //leftIndex是基准值的位置，以它为分界线，看第k大的位置在左边还是右边，进而对相应区域使用快排
        //如果第k大的数已经归位，则返回
        if(leftIndex == nums.length - k){
            num = nums[leftIndex];
            return;
        }else if(leftIndex > nums.length - k){
            quickSelect(nums,k,left,leftIndex - 1);
        }else if(leftIndex < nums.length - k){
            quickSelect(nums,k,leftIndex + 1,right);
        }
    }

    //交换数组中两个数的位置
    public void swap(int[] nums,int index1,int index2){
        int temp = nums[index1];
        nums[index1] = nums[index2];
        nums[index2] = temp;
    }

    /**
     * 调整堆
     * @param nums 数组
     * @param index 所要调整的元素下标
     * @param endIndex 此次调整的范围
     */
    public void adjustHeap(int[] nums,int index,int endIndex){
        //利用挖坑法调整，先保存nums[index]，待找到其应在的位置时，再填充上去
        int temp = nums[index];
        //2 * index + 1是左子结点的下标，所谓调整，就是不断比较父结点与子结点的大小，从而将父结点调整到合适的位置
        for(int i = 2 * index + 1;i <= endIndex;i = 2 * i + 1){
            //先比较左右子结点哪个大，大的那个需要和父节点交换
            if(i + 1 <= endIndex && nums[i + 1] > nums[i]){
                i = i + 1;
            }
            //如果大的那个子结点比父结点大，则交换
            if(nums[index] < nums[i]){
                swap(nums,index,i);
                index = i;//交换以后要记得调整下标
            }else{//如果父结点比两个子结点都大，则调整结束
                break;
            }
        }
        nums[index] = temp;//将坑填上，也就是将父结点放到其应在的位置
    }

    //堆选择
    public int heapSelect(int[] nums,int k){
        int num = 0;//用来记录结果
        //首先建堆，建堆就是从最后一个非叶子结点开始，不断调整，直到根结点
        //最后一个非叶子结点的下标是(nums.length - 2)/2，这个是可以证明的，可以上网查一下
        for(int i = (nums.length - 2)/2;i >= 0;i--){
            adjustHeap(nums,i,nums.length - 1);
        }
        //所谓堆排序，就是不断将堆顶元素交换到堆尾
        //由于交换后破坏了堆，所以每次交换后都需要调整，以满足堆的要求
        //通过把堆顶元素交换到堆尾，并缩小堆尾范围，逐步使数组达到有序的状态
        for(int endIndex = nums.length - 1;endIndex >= 0;endIndex--){
            adjustHeap(nums,0,endIndex);//调整堆
            swap(nums,0,endIndex);//交换堆顶和堆尾
            //如果第k大元素已经归位，则返回
            if(endIndex == nums.length - k){
                num = nums[endIndex];
            }
        }
        return num;
    }
}