算法设计与分析_蓝桥杯题集精选

 

 

最长公共子序列（动态规划必看）

package 算法设计与分析和蓝桥杯;

import java.util.Arrays;
import java.util.Scanner;

/*
动态规划:
最长公共子序列:给予两个序列，求出两个序列按次序的共有子序列。
如:abcdfwwz和alcqdlw的公共子序列是acdw。解题思路是使用动态规划的思想，求大序列的公共子序列可以转为小序列的公共序列，进而知道大序列的
公共子序列。
递推矩阵strAB[i][j]递推公式为
（1） 0   if i=0或j=0
（2） str[i-1][j-1]+1 若i,j>0 strA.charAt(i - 1) == strB.charAt(j - 1)
（3） max(str[i][j-1]+1,str[i-1][j]+1) 若i,j>0 strA.charAt(i - 1) != strB.charAt(j - 1)
 */
public class MaxSequeeze {

    public void getMaxSqueeze(String strA, String strB) {
        String common = "";
        int strAB[][] = new int[strA.length() + 1][strB.length() + 1];
        for (int i = 0; i < strB.length() + 1; i++) {  //公式一
            strAB[0][i] = 0;
        }
        for (int i = 0; i < strA.length() + 1; i++) {
            strAB[i][0] = 0;
        }

        int indexJ = 1;
        for (int i = 1; i < strA.length() + 1; i++) {
            for (int j = indexJ; j < strB.length() + 1; j++) {
                if (strA.charAt(i - 1) == strB.charAt(j - 1)) { //公式二，
                    strAB[i][j] = strAB[i - 1][j - 1] + 1;
                    for (int k = j + 1; k < strB.length() + 1; k++) {
                        strAB[i][k] = strAB[i][j];
                    }
                    break;
                } else {
                    strAB[i][j] = Math.max(strAB[i - 1][j], strAB[i][j - 1]); //公式三
                }
            }
        }

        int indexA = strA.length();
        while (true) {
            if (indexA <= 0) break;
            for (int i = strB.length(); i > 0; i--) {
                if (strAB[indexA][i] == strAB[indexA - 1][i - 1] + 1 && strAB[indexA][i] == strAB[indexA - 1][i] + 1 && strAB[indexA][i] == strAB[indexA][i - 1] + 1) { //对于最长公共序列的某个公共值，一定满足strAB[i][j]比strAB[i-1][j]和strAB[i][j-1]和str[i-1][j-1]大1
                                                                                                                                                                //此时该位置说明是公共序列元素位置
                    common = strA.charAt(indexA-1) + common;
                    break;
                }
            }
            indexA --;
        }


        System.out.println("最长公共子序列的长度为" + strAB[strA.length()][strB.length()]);
        System.out.println("最长公共子序列为" + common);

    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        String strA = scanner.next();
        String strB = scanner.next();
        MaxSequeeze maxSequeeze = new MaxSequeeze();
        maxSequeeze.getMaxSqueeze(strA, strB);
    }
}
/*
  abcdefghijklmn
  abdfrewkasd
  最长公共子序列的长度为5
最长公共子序列为abdefk
 */

批处理作业调度_回溯法_排列树

https://www.cnblogs.com/henuliulei/p/10196118.html

 

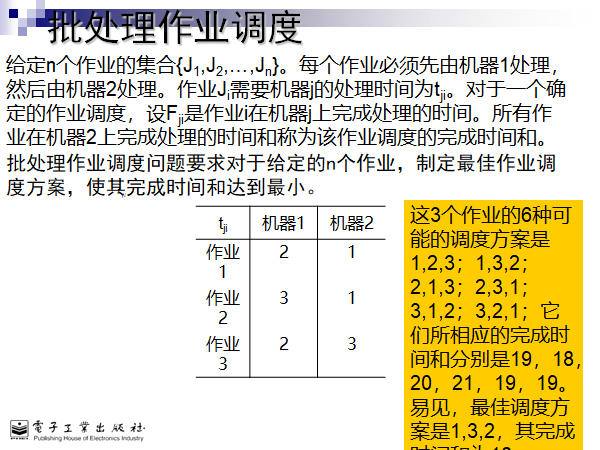
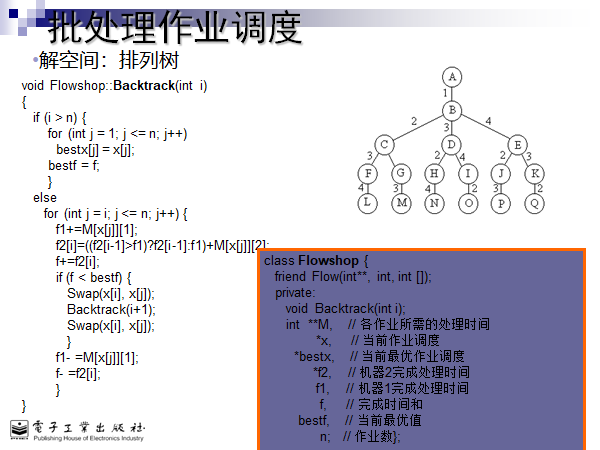
package 算法设计与分析和蓝桥杯;

import 小灰灰.Perm;

import java.util.Arrays;
import java.util.Scanner;

/*
批处理作业调度问题
给定n个作业的集合J={J1,J2,…,Jn}。每一个作业有两项任务分别在两台机器上完成。每个作业必须先由机器1处理，再由机器2处理。作业Ji需要机器j的处理时间为tji，i=1,2,…n，j=1,2。对于一个确定的作业调度，设Fji是作业i在机器j上完成处理的时间。则所有作业在机器2上完成处理的时间和f=F21+F22+…+F2n称为该作业调度的完成时间和。
        批处理作业调度问题要求，对于给定的n个作业，制定最佳的作业调度方案，使其完成时间和最小。
样例输入

3
2 1
3 1
2 3
样例输出
18
1 3 2
 */
public class batchWork {
    static int minValue = Integer.MAX_VALUE;

    void dfs(int level, int num, int work[][], int perm[], int best[]) {

        if (level >= num) {
            int machineA[][] = new int[num][2];     //每个作业在A机器上的工作开始时间和结束时间
            int machineB[][] = new int[num][2];     //每个工作在B机器上的工作开始时间和结束时间
            int timeA = 0;                          //记录机器A已经完成的作业后的时间
            int timeB = 0;                          //记录机器B已经完成的作业后的时间

            for (int i = 0; i < num; i++) {         //根据调度方案计算在机器A上的各个作业的开始和结束时间安排
                machineA[perm[i]][0] = timeA;
                machineA[perm[i]][1] = timeA + work[perm[i]][0];
                timeA = machineA[perm[i]][1];
            }

            int allTime = 0;                        //作业调度的完成时间和

            for (int i = 0; i < num; i++) {         //根据调度方案计算在机器B上的各个作业的开始和结束时间安排
                machineB[perm[i]][0] = Math.max(machineA[perm[i]][1], timeB);       
                machineB[perm[i]][1] = Math.max(machineA[perm[i]][1], timeB) + work[perm[i]][1];
                timeB = machineB[perm[i]][1];
                allTime += timeB;
            }


            if (minValue > allTime) {               //最佳方案
                for (int i = 0; i < num; i++) {
                    best[i] = perm[i];
                }
                minValue = allTime;
            }

        }
        for (int i = level; i < num; i++) {     //常规的全排列代码，也说明这是一个排列树
            int temp = perm[level];
            perm[level] = perm[i];
            perm[i] = temp;

            dfs(level + 1, num, work, perm, best);

            temp = perm[level];
            perm[level] = perm[i];
            perm[i] = temp;
        }
    }

    public static void main(String[] args) {
        int num;
        Scanner scanner = new Scanner(System.in);
        num = scanner.nextInt();
        int work[][] = new int[num][2];  
        for (int j = 0; j < num; j++) {
            work[j][0] = scanner.nextInt();  //在A机器上的工作时间
            work[j][1] = scanner.nextInt();  //在B机器上的工作时间
        }
        int perm[] = new int[num];          //各个作业的一种排序结果，其实就是存储对作业进行调度的每一种方案
        int best[] = new int[num];          //存储最佳调度方案
        for (int i = 0; i < num; i++) {     
            perm[i] = i;
        }
        batchWork batchWork = new batchWork();
        batchWork.dfs(0, num, work, perm, best);
        System.out.println("合理的順序是" + Arrays.toString(best));
        System.out.println("最短時間" + minValue);
    }
}

 

多级调度问题

 

 

 

 

package 算法设计与分析和蓝桥杯;

import java.util.Arrays;
import java.util.Scanner;

/**
 * 多级调度问题，贪心思想，保证各个机器分配的作业时间最够平均来达到时间最短
 * 问题描述：
 * 设有n个独立的作业{1, 2, …, n}, 由m台相同的机器进行加工处理. 作业i所需时间为t i. 约定:任何作业可以在任何一台机器上加工处理, 但未完工前不允许中断处理,任何作业不能拆分成更小的子作业。要求给出一种作业调度方案，使所给的n 个作业在尽可能短的时间内由m台机器加工处理完成。
 * <p>
 * 问题分析：
 * 当作业n的数量小于机器的数量m的时，只需要作业一一分配到每一台机器中，只要把机器i的[0,ti]时间区间分配给作业i即可，所需要的时间便是max[ti]。
 * 当作业n的数量大于机器的数量m的时，应使所有机器尽可能忙碌，首先将n个作业依其所需的处理时间从大到小排序。然后以此顺序将作业分配给空闲的处理机。
 * 假定有7个独立作业，所需处理时间分别为｛2，14，4，16，6，5，3｝，由三台机器M1,M2,M3加工。按照贪心算法产生的作业调度，所需总加工时间为17.
 */
public class ManyMachine {

    static  int getMinindex(int[] machine) {
        int index = 0;
        int minValue = Integer.MAX_VALUE;
        for (int i = 0; i < machine.length; i++) {
            if(machine[i] < minValue){
                minValue = machine[i];
                index = i;
            }
        }
        return index;
    }

    void greedy(int machineNum, int work[]) {
        int[] machine = new int[machineNum];
        Arrays.sort(work);
        for (int i = work.length - 1; i >= 0; i--) {
            int minIndex = ManyMachine.getMinindex(machine);
            machine[minIndex] += work[i];
        }

        int value = 0;
        for (int i = 0; i < machineNum; i++) {
            if(machine[i] >= value){
                value = machine[i];
            }
        }

        System.out.println("调度后所需加工的时间为" + value);
    }

    public static void main(String[] args) {
        int workNum, machineNum;    //作业数，机器数
        Scanner scanner = new Scanner(System.in);
        workNum = scanner.nextInt();
        machineNum = scanner.nextInt();

        int work[] = new int[workNum];
        for (int i = 0; i < workNum; i++) {
            work[i] = scanner.nextInt();
        }

        ManyMachine manyMachine = new ManyMachine();
        manyMachine.greedy(machineNum,work);


    }
}

 最佳调度问题转为深搜问题

最佳调度问题_分支限界法 - 你的雷哥 - 博客园 (cnblogs.com)

 装载问题

 

子集树的特点是每个元素对应树的一行，1,0分别表示是否选择该元素，通过递归回溯来得到满足条件的结果，注意和排列数的不同（排列数n!,每次有多个元素直到1个，所以根据具体问题判断该问题是子集树还是排列树）

 

package 算法设计与分析和蓝桥杯;

import java.util.Arrays;
import java.util.Scanner;

/*
子集树，，，
每一个箱子有两个选择，装和不装，所以是个二叉树，只需要深度搜索找出结果就可以
 */
public class Driver {

    int bestResult = Integer.MIN_VALUE;

    void dfs(int level, int capacity, int[] weight, int x[], int[] best) {
        if (level >= weight.length) {
            System.out.println(Arrays.toString(x));
            int sum = 0;
            for (int i = 0; i < weight.length; i++) {
                sum += x[i] * weight[i];
            }
            if (sum <= capacity && sum > bestResult) {
                bestResult = sum;
                System.arraycopy(x, 0, best, 0, best.length);
            }
        }
        else{
            for (int j = 0; j < 2; j++) {
                x[level] = j;
                dfs(level + 1, capacity, weight, x, best);
            }
        }
    }

    public static void main(String[] args) {
        int capacity;
        int num;
        Scanner scanner = new Scanner(System.in);
        capacity = scanner.nextInt();
        num = scanner.nextInt();
        int[] weight = new int[num];        //箱子的重量
        for (int i = 0; i < weight.length; i++) {
            weight[i] = scanner.nextInt();
        }
        int x[] = new int[num];     //用来记录各个箱子装还是不装
        int best[] = new int[num];     //最优方案
        Driver driver = new Driver();
        driver.dfs(0, capacity, weight, x, best);
        System.out.println("最优装载方案:" + Arrays.toString(best));

    }
}
/*
80 4
18 7 25 36
 */

 

 

 

符号三角形问题

 

 

 (2条消息) 符号三角形_无限迭代中......-CSDN博客_符号三角形

package 算法设计与分析和蓝桥杯;


import base.Prim;

import java.util.Arrays;
import java.util.Scanner;

public class CharacterTriangle {

    static int sum = 0;
    void dfs(int level, int num,int[] character){

        if(num<=level){
//            System.out.println(Arrays.toString(character));
            int [][] Array = new int[num][num];
            for (int i = 0; i < character.length; i++) {
                Array[0][i] = character[i];
            }

            int add = 0;
            int sub = 0;
            for (int i = 0; i < num; i++) {
                if(character[i]==0) add++;
                else sub++;
            }
            for (int i = 1; i < character.length; i++) {
                for (int j = 0; j < character.length-i; j++) {
                    if(Array[i-1][j]==Array[i-1][j+1]){
                        Array[i][j] = 0;
                        add++;
                    }else{
                        Array[i][j] = 1;
                        sub++;
                    }
                }
            }
            if(add==sub) sum++;
        }
          else{
            for (int j = 0; j < 2; j++) {
//                sum ++;

                character[level] = j;
                dfs(level+1,num,character);
            }
        }


    }
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int num = scanner.nextInt();
        int[] character = new int[num];
        CharacterTriangle characterTriangle = new CharacterTriangle();
        characterTriangle.dfs(0,num,character);
        System.out.println(sum);

    }
}

 

n皇后问题

 

 

package 算法设计与分析和蓝桥杯;

import java.util.Arrays;
import java.util.Scanner;

public class NQueen {

    static int sum = 0;
    static  int  ok(int level,int []x){
        int ok = 1;
        for (int i = 0; i < level; i++) {
            if(x[i]==x[level] || Math.abs(i-level)==Math.abs(x[i]-x[level])){
                ok = 0;
            }
        }
        return ok;
    }
    void dfs(int level,int x[]){
        if(level>=x.length){
//            System.out.println(Arrays.toString(x));
            sum++;
        }else{
            for (int i = 0; i < x.length; i++) {
                x[level] = i;
                if(NQueen.ok(level,x)==1)
                    dfs(level+1,x);

            }
        }
    }
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int x[] = new int[n];
        Arrays.fill(x,0);
        NQueen nQueen = new NQueen();
        nQueen.dfs(0,x);
        System.out.println(String.format("共有%d中方案",sum));
    }
}

 

 

 0-1背包问题_回溯法

 

 

package 算法设计与分析和蓝桥杯;

import java.util.Arrays;
import java.util.Scanner;

public class Packet_01 {

    int bestw = 0;

    void dfs(int level, int[] weight, int[] value, int capacity, int x[], int best[], int n, int weightSum) {
        if (level == n) {
            int sumValue = 0;
            for (int i = 0; i < n; i++) {
                sumValue += x[i] * value[i];
            }
            if (sumValue > bestw) {
                bestw = sumValue;
                System.arraycopy(x, 0, best, 0, n);
            }
        } else {
            for (int i = 0; i < 2; i++) {
                if (weightSum + weight[level] * i <= capacity) {
                    x[level] = i;
                    weightSum += weight[level] * i;
                    dfs(level + 1, weight, value, capacity, x, best, n, weightSum);
                }
            }
        }
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int weight[] = new int[n];
        int value[] = new int[n];
        int x[] = new int[n];
        int xBest[] = new int[n];
        for (int i = 0; i < n; i++) {
            weight[i] = scanner.nextInt();
        }
        for (int i = 0; i < n; i++) {
            value[i] = scanner.nextInt();
        }
        int capacity = scanner.nextInt();

        Packet_01 packet_01 = new Packet_01();
        packet_01.dfs(0, weight, value, capacity, x, xBest, n, 0);

        System.out.println("物品选择决策方案是" + Arrays.toString(xBest));
        System.out.println("背包容量有限下，最大价值:" + packet_01.bestw);

    }
}
/*
重量:2 2 6 5 4
价值:6 3 5 4 6
背包容量:10
 */

 

 

图的M着色问题

 

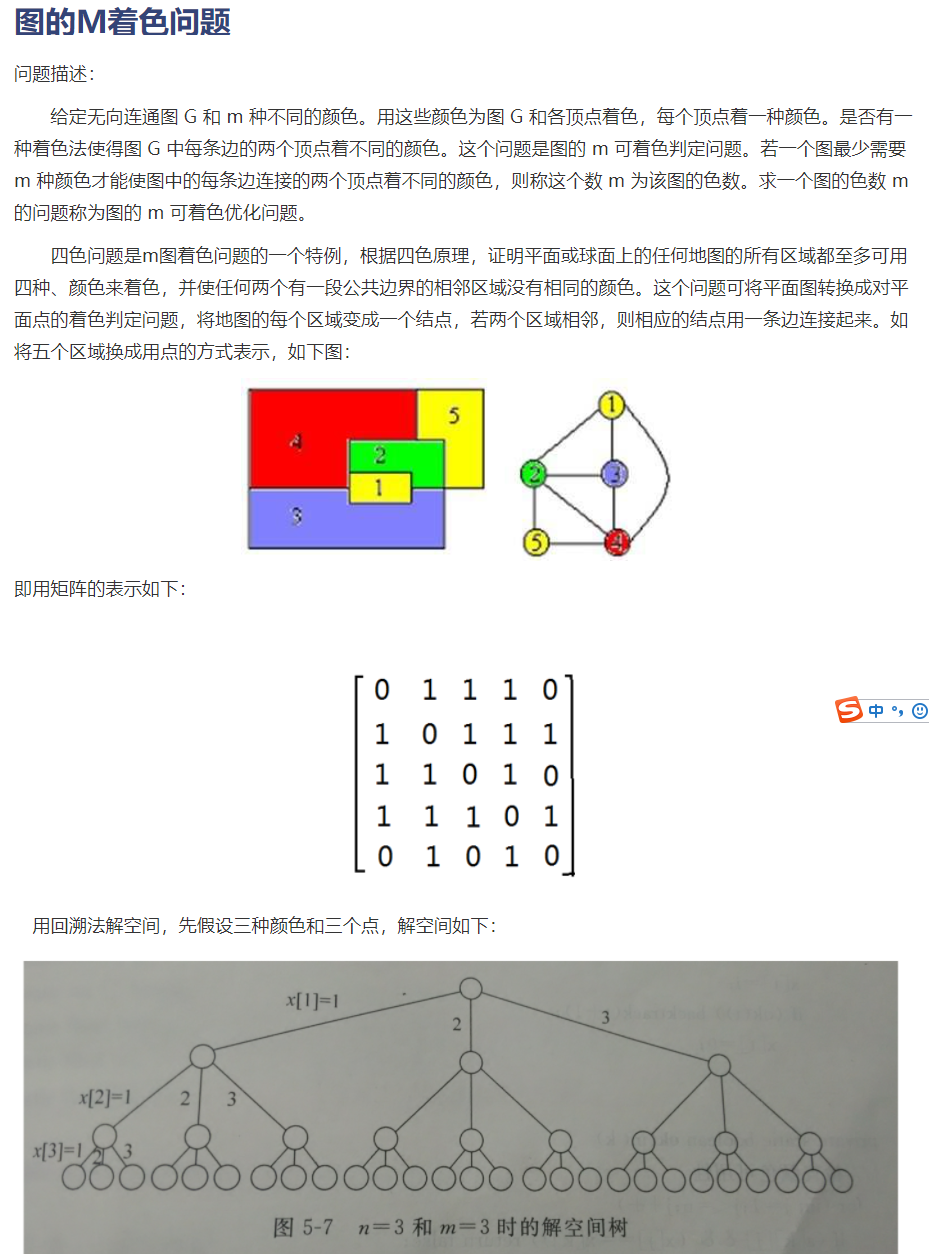
package 算法设计与分析和蓝桥杯;

import java.util.Arrays;
import java.util.Scanner;

public class Mcolor {

    static int judge(int level,int x[],int [][]map){
        int sameColor=0;   //默认周围结点没有相同颜色
        for (int i = 0; i < level; i++) {
            if(map[level+1][i+1]==1){
                if(x[i]==x[level])
                {
                    sameColor=1;
                    break;
                }
                
            }
        }
        return sameColor;
    }
    void colorDfs(int level, int[][] map, int n, int m, int[] x) {
        if(level==n){
            System.out.println("满足条件的一种这色方案: " + Arrays.toString(x));
        }else{
            for (int i = 0; i < m; i++) {
                x[level] = i+1;
                if(judge(level,x,map)==0){
                    colorDfs(level+1,map,n,m,x);
                }
            }
        }
    }

    public static void main(String[] args) {
        int n, m;
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        m = scanner.nextInt();
        int[][] map = new int[n + 1][n + 1];    //连接情况
        int []x = new int[n];   //着色方案
        while (true){   //输入结点连接情况
            int i = scanner.nextInt();
            if(i==-1) break;
            int j = scanner.nextInt();

            map[i][j] = 1;
        }
        Mcolor mcolor = new Mcolor();
        mcolor.colorDfs(0,map,n,m,x);

    }
}

/*
5 4
1 2
1 3
1 4
2 1
2 3
2 4
2 5
3 1
3 2
3 4
4 1
4 2
4 3
4 5
5 2
5 4
-1
 */

 

连续邮资问题

 

 

 

 

 旅行商问题_排列树

 

 

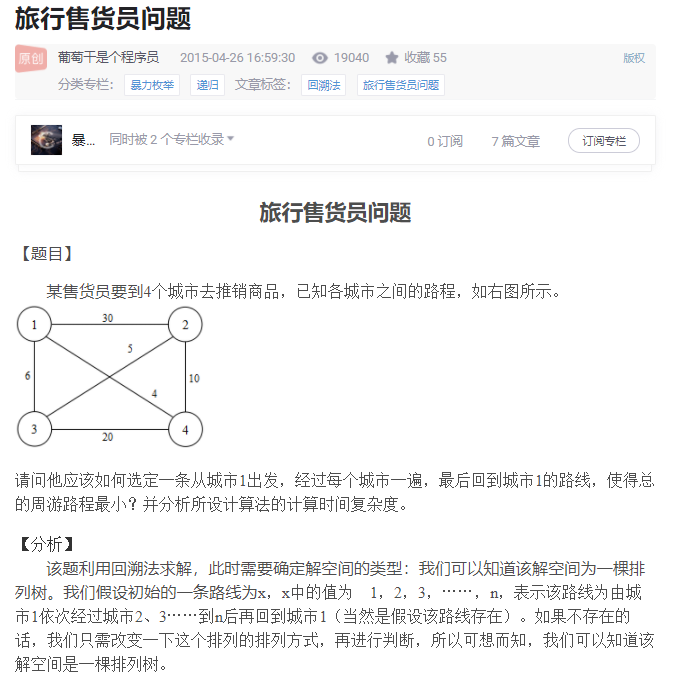
package 算法设计与分析和蓝桥杯;

import java.util.Arrays;
import java.util.Scanner;

public class Market {

    static int sumPath = Integer.MAX_VALUE;//最短总路径

    void merchantDfs(int level, int cityNum, int road[][], int path[],int foot[],int bestPath[]) {//深搜

        if(level==cityNum){
            System.out.println(Arrays.toString(path));
            if(road[path[cityNum-1]][1]>0){
                int sum =0;
                path[level] = 1;
                for (int i = 0; i < path.length; i++) {
                    if(i==path.length-1){
                        sum += road[path[i]][1];
                    }else{
                        sum += road[path[i]][path[i+1]];
                    }

                }
                if(sum < sumPath){
                    sumPath = sum;
                    System.arraycopy(path,0,bestPath,0,path.length);
                }
            }
        }else{
            for (int i = 1; i <= cityNum; i++) {
                if(level==0) {  //保证第一站一定是城市一
                    foot[1] = 1;
                    path[0] = 1;
                    merchantDfs(level+1,cityNum,road,path,foot, bestPath);
                    break;
                }else{
                    if(road[i][path[level-1]]>0 && foot[i]==0){
                        foot[i] = 1;
                        path[level] = i;
                        merchantDfs(level+1,cityNum,road,path,foot, bestPath);
                        foot[i] = 0;
                    }
                }
            }
        }
    }

    void merchantBfs(int level,int cityNum,int road[][], int path[],int bestPath[]){    //广搜
        if(level==cityNum){
            System.out.println(Arrays.toString(path));
            path[path.length-1] = 1;
            boolean isConnection = true;
            for (int i = 0; i <path.length-1; i++) {   //判断路径是否是连同的
                if(road[path[i]][path[i+1]]==0){
                    isConnection = false;
                    break;
                }
            }
            if(isConnection==true){
                int sum = 0;
                for (int i = 0; i < path.length-1; i++) {
                    sum += road[path[i]][path[i+1]];
                }
                if(sum< sumPath){
                    sumPath = sum;
                    System.arraycopy(path,0,bestPath,0,path.length);
                }
            }
        }else{
            for (int i = level+1; i <=cityNum ; i++) {
                if(level==0){
                    path[level] = 1;
                    merchantBfs(level+1,cityNum,road,path,bestPath);
                }else{
                    int temp = path[level];
                    path[level] = path[i-1];
                    path[i-1] = temp;
                    merchantBfs(level+1,cityNum,road,path,bestPath);
                    temp = path[level];
                    path[level] = path[i-1];
                    path[i-1] = temp;
                }

            }
        }
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int cityNum = scanner.nextInt();
        int edge = scanner.nextInt();   //边的个数
        int road[][] = new int[cityNum + 1][cityNum+1];  //城市间的连接情况
        int path[] = new int[cityNum + 1];
        int foot[] = new int[cityNum+1];  //记录该城市是否走过
        int bestPath[] = new int[cityNum+1];
        Arrays.fill(foot,0);
        for (int i = 0; i < path.length; i++) {
            path[i] = i+1;
        }
        for (int i = 0; i < road.length; i++) {
            Arrays.fill(road[i],0);
        }
        int begin = 0;
        int end = 0;
        int roadLength = 0;
        for (int i = 0; i < edge; i++) {
            begin = scanner.nextInt();
            end = scanner.nextInt();
            roadLength = scanner.nextInt();
            road[begin][end] = roadLength;
            road[end][begin] = roadLength;
        }
        Market market = new Market();
//        market.merchantDfs(0,cityNum,road,path,foot,bestPath);
        market.merchantBfs(0,cityNum,road,path,bestPath);
        System.out.println("最佳路线为" + Arrays.toString(bestPath));



    }
}
/*
4 6
1 2 30
1 3 6
1 4 4
2 3 5
2 4 10
3 4 20
 */

 

 单源最短路径_BFS

 

 

 

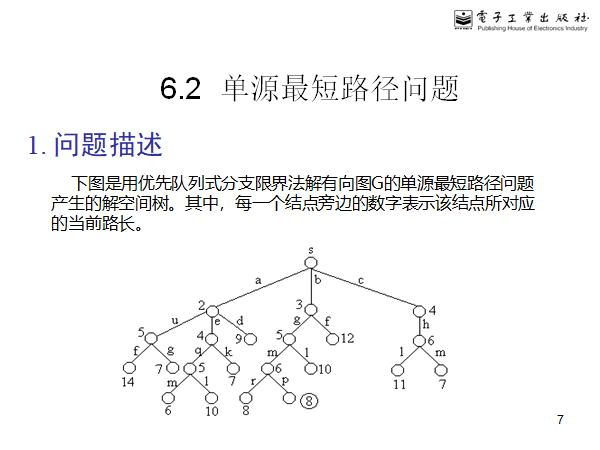
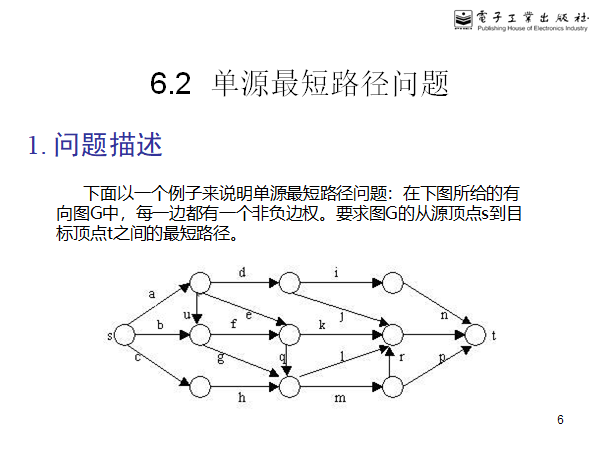
package 算法设计与分析和蓝桥杯;

import java.lang.reflect.Array;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Scanner;
import java.util.concurrent.LinkedBlockingQueue;

public class ShortestPath {

    void bfs(int[][] map, int path[][], int length[]) throws InterruptedException {
        LinkedBlockingQueue<Integer> nodes = new LinkedBlockingQueue<>();
        nodes.put(1);  //假设所有的图起始结点为1,子孙结点和右兄弟结点编号要小于本身，按照层次遍历的顺序编号
        while (true) {
            if (nodes.isEmpty()) break;
            int node = nodes.poll();
            for (int i = node + 1; i < map.length; i++) {     //子孙结点入栈
                if (map[node][i] > 0) nodes.put(i);
            }
            length[node] = Integer.MAX_VALUE;
            for (int i = 1; i < node; i++) {    //找到父节点，计算父节点的总路径长度和到自己的长度和最小的结点是那个

                if (map[i][node] > 0) {
                    if (length[i] + map[i][node] < length[node]) {
                        length[node] = length[i] + map[i][node];
                        for (int j = 1; j <= path[i].length; j++) {
                            if (j == 1) {
                                path[node][j] = 1;  //第一个结点肯定是起始结点
                            } else {
                                if (path[i][j] > 0) {     //父节点的路径
                                    path[node][j] = path[i][j];
                                } else {      //最后一个结点肯定是自己啊
                                    path[node][j] = node;
                                    break;
                                }

                            }

                        }
                    }
                }


            }
        }

    }


    public static void main(String[] args) throws InterruptedException {
        Scanner scanner = new Scanner(System.in);
        int node = scanner.nextInt();
        int edge = scanner.nextInt();
        int a[] = new int[10];
        int map[][] = new int[node + 1][node + 1];      //图
        int begin = 0;
        int end = 0;
        for (int i = 0; i < edge; i++) {
            begin = scanner.nextInt();
            end = scanner.nextInt();
            int len = scanner.nextInt();
            map[begin][end] = len;
            map[end][begin] = len;
        }
        int path[][] = new int[node + 1][node + 1];     //记录每个结点的最短路径
        int length[] = new int[node + 1];     //每个结点的最短路径
//        Arrays.fill(length,Integer.MAX_VALUE);
        ShortestPath shortestPath = new ShortestPath();
        shortestPath.bfs(map,path,length);
        for (int i = 1; i <=node; i++) {
            System.out.println(String.format("结点%d的最短路径的线路是%s",i,Arrays.toString(path[i])));
        }
    }
}
/*
11 16
1 2 2
1 3 4
1 4 6
2 5 2
2 6 4
2 7 10
3 6 8
4 7 8
5 10 2
5 9 10
6 8 2
7 9 3
7 10 4
8 11 3
9 11 2
10 11 1
 */

 先序中序求后序，中序后序求先序

根据前序、中序、后序遍历还原二叉树 - 你的雷哥 - 博客园 (cnblogs.com)

排列组合公式

 

 

 入栈出栈所有可能数

X星球特别讲究秩序，所有道路都是单行线。一个甲壳虫车队，共16辆车，按照编号先后发车，夹在其它车流中，缓缓前行。
路边有个死胡同，只能容一辆车通过，是临时的检查站，如图【p1.png】所示。
X星球太死板，要求每辆路过的车必须进入检查站，也可能不检查就放行，也可能仔细检查。
如果车辆进入检查站和离开的次序可以任意交错。那么，该车队再次上路后，可能的次序有多少种？
为了方便起见，假设检查站可容纳任意数量的汽车。
显然，如果车队只有1辆车，可能次序1种；2辆车可能次序2种；3辆车可能次序5种。 现在足足有16辆车啊，亲！需要你计算出可能次序的数目。

思路：这道题其实是一个进栈出栈的题，也就是问所有出栈顺序的可能数，如果之前了解过这方面的问题的同学，这道题其实就是送分题，可以直接利用卡特兰数的公式求解，不了解的话

可以看一下我之前写的一篇博客，也是关于进出栈次序的问题，有对卡特兰数详细的分析https://www.cnblogs.com/henuliulei/p/9867106.html，下面是几种网上的常见求解思路，做了一下总结

方法一：求出栈次序，无非就是问一共有多少种满足要求的排列，满足条件在本题中就是指，只有站中有“车”，才能够出来。假设1，代表进站，0代表出站，r代表进栈的个数，L代表出栈的个数，易知

只有进栈的个数r大于等于出栈的个数L才可以出栈或进栈，否则只能进栈,因此可以进行回溯求出所有可能的方案。

#include<iostream>

using namespace std;

int num=0;



void dfs(int n,int r,int l){

    if(n==32){

        num++;

        return;

    }



        if(r>l){

            if(r<16)

            dfs(n+1,r+1,l);

            if(l<16)

            dfs(n+1,r,l+1);

        }else{

            if(r==l)

            if(r<16)

            dfs(n+1,r+1,l);

        }



    return;

}



int main(){



    dfs(0,0,0);

    cout<<num<<endl;

    return 0;

}

方法二：利用卡特兰数的公式f(n) = f(0)*f(n-1) + f(1)*f(n-2) + ... +f(n-1)*f(0)

 

 这个问题也是转换为求进栈出栈的问题，记住卡特兰数算法提高效率，深搜作为备选方案，不过一个问题是当n较大时，可能的方案就远超int的范围了，可以考虑大整数.

BF算法和kmp

字符串的模式匹配 - 你的雷哥 - 博客园 (cnblogs.com)

void BF(string str1,int stra,string str2,int strb,int k,int pos)
{
    int i=pos;
    int j=0;
    //cout << i << strb <<"---" <<endl;
    while(i<stra && j<strb){
        if(str1[i]==str2[j]){
            i++;
            j++;
        }else
        {
            i=i-j+1;
            j=0;
        }
    }
    if(j>=strb){
        num[k]++;
        pos=i-strb+1;
        if(pos<=stra-strb){
            BF( str1, stra, str2, strb,k, pos);
        }
    }
}
void get_next(string str,int stra)
{
    int i=1;
    next[1]=0;
    int j=0;
    while(i<stra){
        if(j==0 || str[i]==str[j]){
            i++;
            j++;
            next[i]=j;
        }else{
            j=next[j];
        }
    }
}
int KMP(string a,int stra,string b,int strb,int k,int pos)
{
    int i=pos;
    int j=1;
    while(i<stra && j<=strb){
        if(j==0 || a[i]==b[j-1]){
            i++;
            j++;
        }else{
            j=next[j];
        }
    }
    if(j>strb){
        num1[k]++;
        pos=i-strb+1;
    //    cout << pos << " =pos" << endl;
        if(pos<=stra-strb){
            KMP(a,stra,b,strb,k,pos);
        }
    }
}

非常nice的一道递归题，有空可以自己再写一遍

最大k乘积 - 你的雷哥 - 博客园 (cnblogs.com)

nim博弈问题

历届试题 高僧斗法 - 你的雷哥 - 博客园 (cnblogs.com)

并查集

数据结构_并查集（转载） - 你的雷哥 - 博客园 (cnblogs.com)

历届试题 合根植物 - 你的雷哥 - 博客园 (cnblogs.com)

一道练习深搜的题

历届试题 大臣的旅费 - 你的雷哥 - 博客园 (cnblogs.com)

扩展欧几里得

小明开了一家糖果店。他别出心裁：把水果糖包成4颗一包和7颗一包的两种。糖果不能拆包卖。

小朋友来买糖的时候，他就用这两种包装来组合。当然有些糖果数目是无法组合出来的，比如要买 10 颗糖。

你可以用计算机测试一下，在这种包装情况下，最大不能买到的数量是17。大于17的任何数字都可以用4和7组合出来。

本题的要求就是在已知两个包装的数量时，求最大不能组合出的数字

 

 

 

 

 

 

Java实现字符串反转

 

　　总结一道 Java 面试常见编程题：将 'abc123' 字符串反转，把你能想到的方法都写下来。

　　1. 利用 StringBuffer 或 StringBuilder 的 reverse 成员方法:

  // StringBuffer
  public static String reverse1(String str) {
    return new StringBuilder(str).reverse().toString();
  }

　　2. 利用 String 的 toCharArray 方法先将字符串转化为 char 类型数组，然后将各个字符进行重新拼接:

  // toCharArray
  public static String reverse2(String str) {
    char[] chars = str.toCharArray();
    String reverse = "";
    for (int i = chars.length - 1; i >= 0; i--) {
      reverse += chars[i];
    }
    return reverse;
  }

　　3. 利用 String 的 CharAt 方法取出字符串中的各个字符:

  // charAt
  public static String reverse3(String str) {
    String reverse = "";
    int length = str.length();
    for (int i = 0; i < length; i++) {
      reverse = str.charAt(i) + reverse;
    }
    return reverse;
  }

 

全排列+

 

 

 

 半数集

给定一个自然数n，由n 开始可以依次产生半数集set(n)中的数如下。
(1) n∈set(n)；
(2) 在n 的左边加上一个自然数，但该自然数不能超过最近添加的数的一半；
(3) 按此规则进行处理，直到不能再添加自然数为止。
例如，set(6)={6,16,26,126,36,136}。半数集set(6)中有6 个元素

#include<bits/stdc++.h>
using namespace std;
int sum = 1;
void f(int n)
{
    for(int i=1;i<=n/2;i++){
        sum ++;
        f(i);
    }
}
int main()
{
    int n;
    cin >> n;
    f(n);
    cout << sum << endl;

}

集合划分的解法

int f(int n,int m)
{
    if(n==1) return 1;//只有一个集合
    if(m==m) return 1;//每个元素一个集合
    else{
        return m*f(n-1,m)+f(n-1,m+1);//向n-1个元素划分的m个集合里添加一个新元素，有m*f（n-1,m）种，
    }                                    //向n-1个元素划分的m个集合里添加一个独立元素，有f（n-1,m+1）种，

}

 整数因子分解问题 

´问题描述： 
大于1 的正整数n 可以分解为：n=x1 *x 2*…*xm 。                            
例如，当n= 12 时，共有8 种不同的分解式： 
12= 12； 
12=6*2； 
12=4*3； 
12=3*4； 
12=3*2*2； 
12=2*6； 
12=2*3*2； 
12=2*2*3。

void f(n)
{
    if(n==1) num+=1;
    for(int i=2;i<=n;i++){
        if(n%i==0) f(n/i);
    }
}

利用二分法求最大值

#include<bits/stdc++.h>
using namespace std;
int getMax(int array[],int begin,int end)
{
if(begin==end) return array[end];
int mid=(begin+end)/2;
int max1=getMax(array,begin,mid);
int max2=getMax(array,mid+1,end);
return max1>max2?max1:max2;
}
int main()
{
int array[15]={18,1,3,5,7,9,7,5,3,4,11,44,5,3};
cout << getMax(array,0,13);
return 0;
}

最大字段和

    static  void maxPeriod(int array[]){
        int period = array[0];
        int sum = period;
        for (int i = 1; i < array.length; i++) {
            if(period >= 0) period+= array[i];
            if(period < 0) period = array[i];
            if(period > sum) sum = period;
        }
        System.out.println(sum);
    }

 挺有意思的一道深搜题

历届试题 剪格子 - 你的雷哥 - 博客园 (cnblogs.com)

数字三角形（考察了递归和递推，因为递归计算中包含了重复计算，使用了备忘录大大提高了效率，递推的出现使得指数级的计算变为线性）

数字三角形 - 你的雷哥 - 博客园 (cnblogs.com)

正整数分解使得乘积最大问题(转载，看看就行)