Redis笔记2

setnx的分布式锁

使用Redis的 SETNX 命令可以实现分布式锁，下文介绍其实现方法。

SETNX命令简介

命令格式

SETNX key value

将 key 的值设为 value，当且仅当 key 不存在。 
若给定的 key 已经存在，则 SETNX 不做任何动作。 
SETNX 是SET if Not eXists的简写。

返回值

返回整数，具体为 
- 1，当 key 的值被设置 
- 0，当 key 的值没被设置

例子

redis> SETNX mykey “hello” 
(integer) 1 
redis> SETNX mykey “hello” 
(integer) 0 
redis> GET mykey 
“hello” 
redis>

使用SETNX实现分布式锁

多个进程执行以下Redis命令：

SETNX lock.foo <current Unix time + lock timeout + 1>

如果 SETNX 返回1，说明该进程获得锁，SETNX将键 lock.foo 的值设置为锁的超时时间（当前时间 + 锁的有效时间）。 
如果 SETNX 返回0，说明其他进程已经获得了锁，进程不能进入临界区。进程可以在一个循环中不断地尝试 SETNX 操作，以获得锁。

解决死锁

考虑一种情况，如果进程获得锁后，断开了与 Redis 的连接（可能是进程挂掉，或者网络中断），如果没有有效的释放锁的机制，那么其他进程都会处于一直等待的状态，即出现“死锁”。

上面在使用 SETNX 获得锁时，我们将键 lock.foo 的值设置为锁的有效时间，进程获得锁后，其他进程还会不断的检测锁是否已超时，如果超时，那么等待的进程也将有机会获得锁。

然而，锁超时时，我们不能简单地使用 DEL 命令删除键 lock.foo 以释放锁。考虑以下情况，进程P1已经首先获得了锁 lock.foo，然后进程P1挂掉了。进程P2，P3正在不断地检测锁是否已释放或者已超时，执行流程如下：

  • P2和P3进程读取键 lock.foo 的值，检测锁是否已超时（通过比较当前时间和键 lock.foo 的值来判断是否超时）
  • P2和P3进程发现锁 lock.foo 已超时
  • P2执行 DEL lock.foo命令
  • P2执行 SETNX lock.foo命令，并返回1，即P2获得锁
  • P3执行 DEL lock.foo命令将P2刚刚设置的键 lock.foo 删除（这步是由于P3刚才已检测到锁已超时）
  • P3执行 SETNX lock.foo命令，并返回1，即P3获得锁
  • P2和P3同时获得了锁

从上面的情况可以得知，在检测到锁超时后，进程不能直接简单地执行 DEL 删除键的操作以获得锁。

为了解决上述算法可能出现的多个进程同时获得锁的问题，我们再来看以下的算法。 
我们同样假设进程P1已经首先获得了锁 lock.foo，然后进程P1挂掉了。接下来的情况：

  • 进程P4执行 SETNX lock.foo 以尝试获取锁
  • 由于进程P1已获得了锁，所以P4执行 SETNX lock.foo 返回0，即获取锁失败
  • P4执行 GET lock.foo 来检测锁是否已超时，如果没超时，则等待一段时间，再次检测
  • 如果P4检测到锁已超时，即当前的时间大于键 lock.foo 的值，P4会执行以下操作 
    GETSET lock.foo <current Unix timestamp + lock timeout + 1>
  • 由于 GETSET 操作在设置键的值的同时，还会返回键的旧值，通过比较键 lock.foo 的旧值是否小于当前时间，可以判断进程是否已获得锁
  • 假如另一个进程P5也检测到锁已超时，并在P4之前执行了 GETSET 操作，那么P4的 GETSET 操作返回的是一个大于当前时间的时间戳，这样P4就不会获得锁而继续等待。注意到，即使P4接下来将键 lock.foo 的值设置了比P5设置的更大的值也没影响。

另外，值得注意的是，在进程释放锁，即执行 DEL lock.foo 操作前，需要先判断锁是否已超时。如果锁已超时，那么锁可能已由其他进程获得，这时直接执行 DEL lock.foo 操作会导致把其他进程已获得的锁释放掉。

程序代码

用以下python代码来实现上述的使用 SETNX 命令作分布式锁的算法。

LOCK_TIMEOUT = 3
lock = 0
lock_timeout = 0
lock_key = 'lock.foo'
 
# 获取锁
while lock != 1:
    now = int(time.time())
    lock_timeout = now + LOCK_TIMEOUT + 1
    lock = redis_client.setnx(lock_key, lock_timeout)
    if lock == 1 or (now > int(redis_client.get(lock_key))) and now > int(redis_client.getset(lock_key, lock_timeout)):
        break
    else:
        time.sleep(0.001)
 
# 已获得锁
do_job()
 
# 释放锁
now = int(time.time())
if now < lock_timeout:
    redis_client.delete(lock_key)

 

Redis有序集合Zset的底层数据结构：跳跃表（跳表，skip list）

1 为什么引入跳跃表
我们知道红黑树是一种存在于内存中，可以保证在最坏的情况下，对红黑树进行例如search，insert，以及delete等基本的动态集合操作的时间复杂度为O(lg n)。

但是显而易见，红黑树实现起来比较复杂，尤其是对红黑树进行insert和delete操作。并且在红黑树中进行范围查询时需要对红黑树进行中序遍历，这也是比较复杂的操作。

那有没有一种能确保对动态集合search，insert以及delete等操作的时间复杂度在O(lg n)的前提下，实现比较简单，还能比较方便的进行范围查询的数据结构呢？

答案是肯定的，就是我们今天要总结的数据结构——跳跃表（skip list）。

2 引入的过程
例子：假设我们在内存中有一个长度达到10万以上的一个已经排好序的链表结构。我们要往这个链表结构中插入一个元素。我们是怎么进行插入的呢？

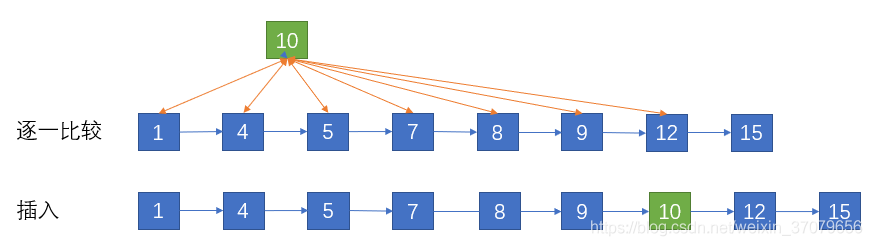
来看下图所示的这个列表（为了使链表结构简单，图中只画出了8个元素：1，4，5，7，8，9，12，15）：

 

 

 

上图所示链表中，各元素按照升序排列，现在要在该链表中插入元素10，首先要确定元素10应该插入的位置，如下图所示。

由于是链表结构因此无法使用二分查找算法，只能和原链表中的结点逐一比较大小来确定位置。这一步的时间复杂度是O(N)。

插入的过程到时很容易，直接改变结点指针的目标，时间复杂度是O(1)。

因此总体的时间复杂度是O(N)。

 

 

 

这对于拥有上十万的集合来说，这种办法显然太慢了。那有什么办法可以让search，insert以及delete操作性能更高一点呢？

search，insert以及delete操作其实归根结底就是search太慢的问题。所以只要search操作变快insert和delete操作也会变快。

让我们来回想一下MySQL索引。

所谓的索引就是把数据库表中的一些特定信息提取出来，缩小查询操作时的搜索范围，来提升查询性能。

那我们是不是可以借鉴数据库索引的思想，提取出链表中的部分关键结点。

还以上面的例子，那么我们可以取出所有值为奇数的结点作为关键结点。

 

 

 

此时如果要插入一个值为10的新节点，不再需要和原结点1，4，5，7，8，9，12逐一进行比较，只需要比较关键结点1，5，7，9，15即可。

 

 

 

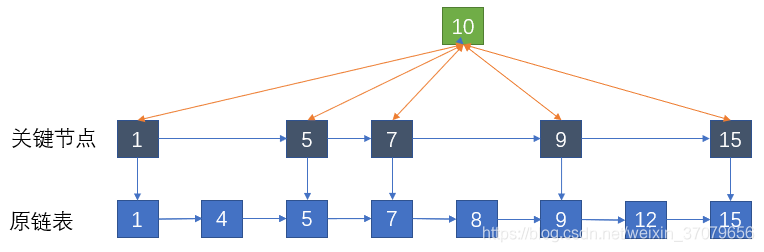
确定了新结点在关键结点中的位置（9和15之间），就可以回到原链表，迅速定位到对应的位置插入（同样是9和15之间）。

 

 

 

 

 

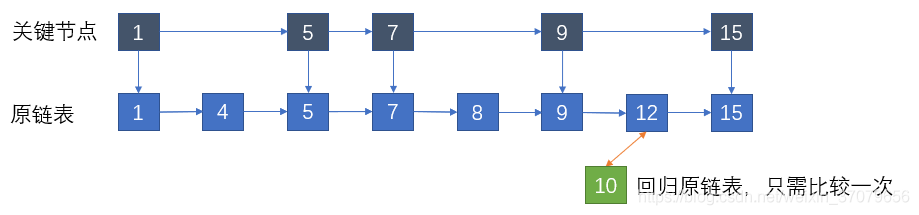
节点数目少，优化效果不是很明显，如果是十万个结点，比较次数就整整减少了一半！也就是说虽然增加了50%的额外的空间，但是性能提高了一倍。

不过我们可以进一步思考。既然已经提取出了一层关键结点作为索引，那我们为何不能从索引中进一步提取，提出一层索引的索引？

 

 

 

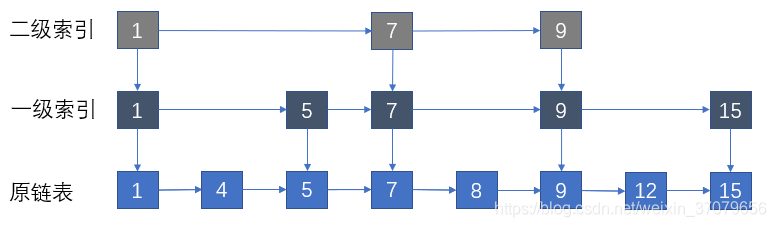
有了2级索引之后，新的结点可以先和2级索引比较，确定大体范围之后在和1级索引进行比较，最后再回到原链表，找到并插入对应位置。

当结点很多的时候，比较次数就会减少到原来的四分之一！当节点足够多的时候，我们可以不止提出两层索引，还可以向更高层次提取，保证每一层是上一层结点数的一半。

提取的极限就是同一层只有两个结点的时候，因为一个结点没有比较的意义。这样的多层链表结构就是所谓的跳跃表。

3 跳跃表的基本概念
跳跃表是将链表改造支持二分法查找的数据结构 。

如果是一个单链表的话，他查找数据的时间复杂度为O(n)，于是给单链表添加一级索引每两个节点提取一个节点到上一级，我们把诌出来的哪一级叫做索引或者索引层，如下图：

 

 

 

当你查找12的时候，你只需要遍历6次就可以得到结果值 ，

先去第一层索引查到，遍历到9的时候发现下一个节点是15那我们就知道此时12就在这两个节点之间，所以我们进行down进入下一层

继续遍历这个时候我们只需要遍历两个节点就可以找到了，所以我们遍历12在建立上层索引的情况下是只需要遍历7次，但是单链表便利需要7次，那我们在继续添加及层索引如下图:

 

 

 

当有64个节点的链表的时候，则会创建多少层索引，通过计算会有5层，那么每一层的索引个数有 （n为总的索引树，k为创建的索引层数（不包括原始链表数据结构））,

最高的层的索引层的长度为2，那我们计算出 层级为 ，

如果我们每一层遍历M个元素那么我们的时间复杂度为 ,

我们的是两个元素结合为一个节点那么每一层最多遍历3个元素，那么我们时间复杂度为 那么时间复杂度为

现在就是在原有的得单链表上创建了多层索引而达到二分法查找，达到很高。

那么现在这样岂不是浪费了很多的内存（空间换用时间）。

有一个问题需要注意：

当大量的新节点通过逐层比较，最终插入到原链表之后，上层的索引结点会渐渐变得不够用。

这时候需要从新结点中选取一部分提到上一层。

可是究竟应该提拔谁呢？

这可能是随机选取（也叫抛硬币，50%的可能性会被提拔，50%的可能性不会被提拔）的，也可能是根据某些规则确定性的选取，其中随机选取更加常见（因为跳跃表的元素删除和添加是不可预测的，很难用一种有效的算法来保证跳跃表的索引分布始终均匀，随机选取虽然不能保证索引绝对均匀分布，却可以大体上趋于均匀）。

下面以随机选取为例进行说明，比如给定一个长度是7的有序链表，结点值一次是1，2，3，5，6，7，8。

那么我们可以取出所有值为奇数的结点作为关键结点。假如值为9的新节点插入原链表：

 

 

 

 

 

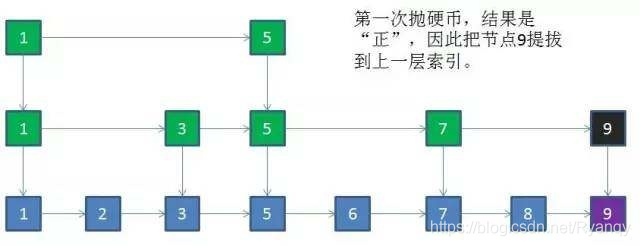
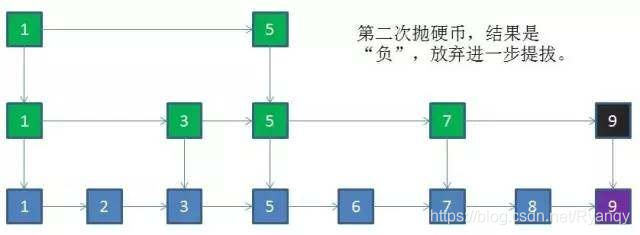
4 跳跃表的更新
4.1 跳跃表插入节点
具体看上面的分析，这里就不再一一赘述。

跳跃表插入节点的流程有以下几步：

  • 新结点和各层索引结点逐一比较，确定原链表的插入位置，时间复杂度是O(logN)。
  • 把索引插入到原链表，时间复杂度是O(1)。
  • 利用抛硬币的随机方式，决定新结点是否提升到上一级索引。结果为正则提升，并且继续抛硬币，结果为负则停止，时间复杂度是O(logN)。

总体上，跳跃表插入操作的时间复杂度是O(logN)，而这种数据结构所占空间是2N。

4.2 跳跃表删除节点
跳跃表的删除操作比较简单，只要在索引层找到要删除的结点，然后顺藤摸瓜，删除每一层的相同结点即可。

这里还以一个长度是7的有序链表为例，结点值一次是1，2，3，5，6，7，8。取出所有值为奇数的结点作为关键结点。

如果某一层索引在删除后只剩下一个结点，那么整个一层就可以干掉了。例如要删除结点的值是5：

 

 

 

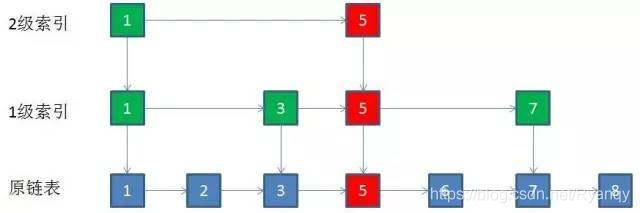
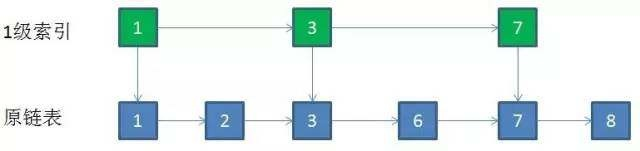
我们来总结一下跳跃表删除结点的操作步骤：

  • 自上而下，查找第一次出现结点的索引，并逐层找到每一层对应的结点（因为每层索引都是由上层索引晋升的），时间复杂度是O(logN)。
  • 删除每一层查找到的结点，如果该层只剩下一个结点，删除整个一层，时间复杂度是O(logN)。

总体上，跳跃表删除操作的时间复杂度是O(logN)。

从上面的总结可以看出，相对于红黑树来说，由于跳跃表维持结构平衡的成本比较低，完全依靠随机。而红黑树在多次插入和删除后，需要rebalance来重新调整结构平衡。
对于redis单线程的理解

https://zhuanlan.zhihu.com/p/128598311

 

 

https://www.icode9.com/content-2-688011.html

 

 

阻塞I/O、非阻塞I/O和I/O多路复用

 

 

 

 

posted @ 2021-06-23 20:10  你的雷哥  阅读(65)  评论(0)  编辑  收藏  举报