残差网路详解
转自：https://zhuanlan.zhihu.com/p/72679537
残差网络在设计之初，主要是服务于卷积神经网络(CNN)，在计算机视觉领域应用较多，但是随着CNN结构的发展，在很多文本处理，文本分类里面(n-gram)，也同样展现出来很好的效果。
首先先明确一下几个深度学习方面的问题？
网络的深度为什么重要？
我们知道，在CNN网络中，我们输入的是图片的矩阵，也是最基本的特征，整个CNN网络就是一个信息提取的过程，从底层的特征逐渐抽取到高度抽象的特征，网络的层数越多也就意味这能够提取到的不同级别的抽象特征更加丰富，并且越深的网络提取的特征越抽象，就越具有语义信息。
为什么不能简单的增加网络层数？
对于传统的CNN网络，简单的增加网络的深度，容易导致梯度消失和爆炸。针对梯度消失和爆炸的解决方法一般是正则初始化(normalized initialization)和中间的正则化层(intermediate normalization layers)，但是这会导致另一个问题，退化问题，随着网络层数的增加，在训练集上的准确率却饱和甚至下降了。这个和过拟合不一样，因为过拟合在训练集上的表现会更加出色。
在我参考的博客中，作者针对“退化问题”做了实验并得出如下结论：
按照常理更深层的网络结构的解空间是包括浅层的网络结构的解空间的，也就是说深层的网络结构能够得到更优的解，性能会比浅层网络更佳。但是实际上并非如此，深层网络无论从训练误差或是测试误差来看，都有可能比浅层误差更差，这也证明了并非是由于过拟合的原因。导致这个原因可能是因为随机梯度下降的策略，往往解到的并不是全局最优解，而是局部最优解，由于深层网络的结构更加复杂，所以梯度下降算法得到局部最优解的可能性就会更大。
如何解决退化问题
这里提供了一种想法：既然深层网络相比于浅层网络具有退化问题，那么是否可以保留深层网络的深度，又可以有浅层网络的优势去避免退化问题呢？如果将深层网络的后面若干层学习成恒等映射 ，那么模型就退化成浅层网络。但是直接去学习这个恒等映射是很困难的，那么就换一种方式，把网络设计成：
只要 就构成了一个恒等映射
，这里
为残差。
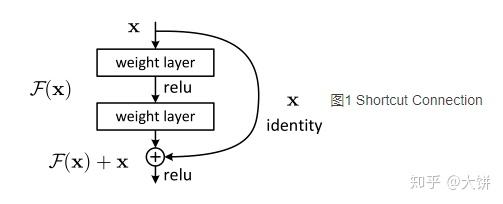
Resnet提供了两种方式来解决退化问题：identity mapping以及residual mapping。identity mapping指的是图中“弯线”部分，residual mapping指的是非“弯线”的剩余部分。 是求和前网络映射，
是输入到求和后的网络映射。
博客中作者举了这样一个例子：假设有个网络参数映射： 和
，这里想把5映射成5.1，那么
，引入残差的映射
。引入残差的映射对输出的变化更加敏感，比如从输出的5.1再变化到5.2时，映射
的输出增加了1/51=2%。而残差结构输出的话，映射
从0.1到0.2，增加了100%。明显后者的输出变化对权重的调整作用更大，所以效果更好。
这种残差学习结构通过前向神经网络+shortcut链接实现，其中shortcut连接相当于简单执行了同等映射，不会产生额外的参数，也不会增加计算复杂度。整个网络依旧可以通过端到端的反向传播训练。
公式推导
残差结构的公式表达：
通过递归，可以得到任意深层单元L特征的表达：
对于任意深的单元L的特征 可以表达为浅层单元l的特征
加上一个形如
的残差函数，表明了任何单元L和l之间都具有残差特性。
同样的，对于任意深的单元L，它的特征 ，即为之前所有残差函数输出的总和再加上
。
对于反向传播，假设损失函数为E，根据反向传播的链式法则可以得到：
式子被分为两个部分：
- 不通过权重层的传递
- 通过权重层的传递：
前者保证了信号能够直接传回到任意的浅层 ，同时这个公式也保证了不会出现梯度消失的现象，因为
不可能为-1。
ResNet结构
连接方式："shortcut connection"
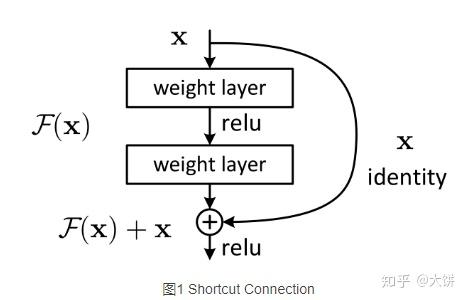
- shortcut同等维度映射，
与
相加就是逐元素相加
- 如果两者维度不同，需要给
卷积层进行残差学习：以上公式都是基于全连接层的，实际上可以使用卷积层，加法随之变为对应channel间的两个feature map逐元素相加。
- 对于输出feature map大小相同的层，有相同数量的filters，即channel数相同。
- 当feature map大小减半时(池化)，filters数量翻倍。对于残差网络，维度匹配的shortcut连接为实线，反之为虚线。维度不匹配时，同等映射有两种可选方案：
- 直接通过zero padding来增加维度(channel)。
- 乘以W矩阵投影到新的空间。实现是用1x1卷积实现的，直接改变1x1卷积的filters数目，这种会增加参数。
博客作者针对两种方法做了实验比较：发现投影法会比zero padding表现稍微好一些，因为zero padding的部分没有参与残差学习。实验证明，将维度匹配或不匹配的同等映射全用投影法会取得更好的结果，但是考虑到不增加复杂度和参数的前提下，这种方式则不适用。
关于网络结构的一些细节问题
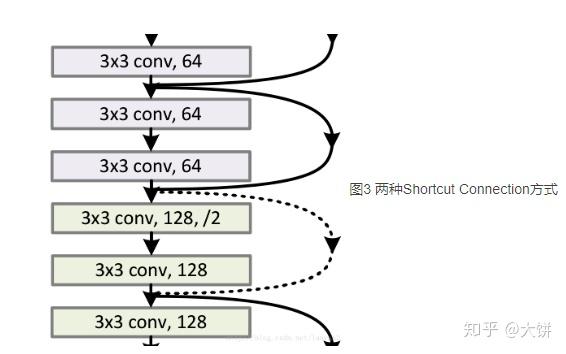
(1)如果F(x)和x的channel个数不同，如何进行F(x)和x的维度相加？
?
实线的connection部分，即第1个和第3个矩阵之间都是执行3x3x64的卷积，channel个数一致，计算方式：
虚线的connection部分，第3个矩阵和第5个矩阵分别是3x3x64和3x3x128的卷积操作，他们的channel个数不同(64和128)，采用计算方式：
其中W是卷积操作(用128个(3x3x64)的filter)，用来调整x的channel维度。
计算细节
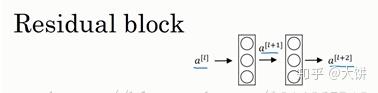
这里引入一个两层神经网络，
为激活函数，例如relu。
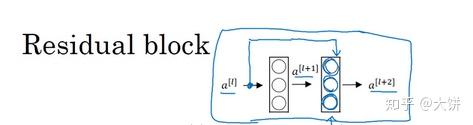
在残差网络中，将 直接加到
之后，下一次激活函数
之前，那么
,加上了的这个产生了残差块。
网络以及1x1的卷积
1x1卷积核的作用请参考我的另一篇文章《深度学习——卷积神经网络》。
ResNet50和ResNet101
这两个网络结构是目前比较流行的，给出它们具体的结构：
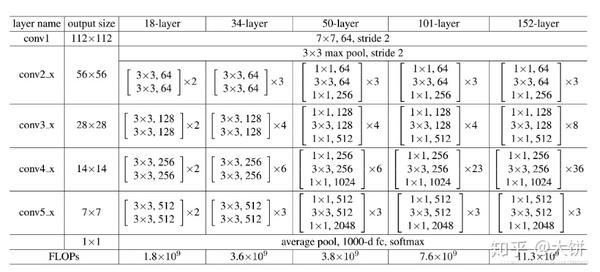
上面是5种深度的ResNet，分别是18,34,50,101和152，拿ResNet50来看：第一层为7x7x64的卷积，然后是3+4+6+3=16个building block，每个block为3层，所以有16x3=48层。最后有个fc层，所以总共为1+1+48=50层。
普通的平原网络与深度残差网络的最大区别在于，深度残差网络有很多旁路的支线将输入直接连到后面的层，使得后面的层可以直接学习残差，这些支路就叫做shortcut。传统的卷积层或全连接层在信息传递时，或多或少会存在信息丢失、损耗等问题。ResNet 在某种程度上解决了这个问题，通过直接将输入信息绕道传到输出，保护信息的完整性，整个网络则只需要学习输入、输出差别的那一部分，简化学习目标和难度。
