T-sne降维

1. SNE原理

基本原理： 是通放射变换  将数据点映射到概率分布上，分为两个步骤：

  • 构建高维对象之间的概率分布，使得相似的对象有更高的概率被选择，而不相似的对象有更低的概率。
  • SNE 在低维空间中构建这两个分布，使得两个概率分布尽可能相似。

t-SNE是非监督的降维，跟kmeans 等不同，他不能通过训练得到一些东西后再用于其他数据（kmeans 可以通过训练得到k个点，再用于其他数据集，而t-SNE 只能单独多数据做操作。

原理推导： SNE 是先将欧几里得距离转化为条件概率来表达点与点之间的相似度，具体来说，给定N个高 维的数据，（N 不是维度）。首先是计算概率pij，正比于xi和xj 之间的相似度，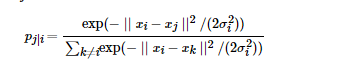

这里的参数对于不同的xi的取值不一样，后续讨论如何设置，此外设置px|x =0，因为我们关注的是两两之间的相似度，对于低维度下的yi，可以指定高斯分布方差为,因此相似度为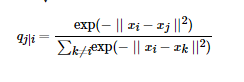

同样qi|i=0。

如果降维效果比较好，局部特征保留完整，那么，因此我们优化两个分布之间的KL散度。目标函数如下：

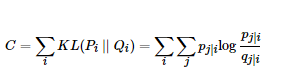，这里的·Pi表示了给定点xi下，其他所有数据点的条件概率分布。

KL 散度具有不对称性，在低维映射中不同距离对应的惩罚权重是不同的。具体来说是： 距离较远的两个点来表达距离较近的两个点会产生更大的cost，距离较近的两个点来表达距离较远的两个点产生的cost 相对较小。例如来建模 cost=

，用同样较大的来建模，因此，SNE 倾向与保留数据中的局部特征。

2 t-SNE

SNE 很难优化，存在Crowing 问题 (拥挤） 不同点： 使用对称的SNE，简化梯度公式，低维空间下，使用更重长尾分布的t 分布替代高斯分布代表两点之间的相似度。来避免拥挤问题。

2.1  Symmetric SNE

优化pi|j 和qi|j 的KL散度的替换思路是使用联合概率分布来替换条件概率分布，即P是高维空间中各个点的联合概率分布，Q是低维空间下的，目标函数为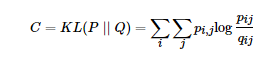

这里1的pii和qii都为0，这种SNE称为symmetric SNE，因为他假设了对于任意i，pij =pji，qij=qji，因此概率分布可以改写为：

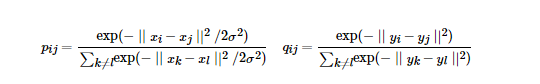
这种方法会引入异常值的问题，比如xi 是异常值，那么||xi-xj||2 会很大，对应的所有的j，pij 都会很小，导致低维映射下yi对cost的影响很小。为了解决这个问题，会将联合概率分布做一个修正。

2.2 Crowing 问题

各个簇聚在一起，无法区分，比如高维数据在降维到10维下，会有很好的表达，但是降维到2维后，无法得到可信映射。

如何解决： 用sight repulsion的方法

2.3 t-SNE

对称SNE时间上在高维度下，另一种减轻拥挤问题的方法： 在高维空间下使用高斯分布将距离转换为概率分布，在低维空间下，使用t 分布将距离转换为概率分布，使得高维度下中低等的距离在映射后能够有个较大的距离。

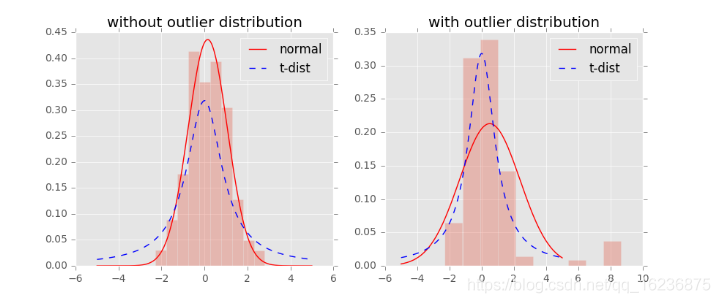
t 分布受异常值影响更小，拟合介个更为合理，较好的捕获了数据的整体特征。

t-SNE 的梯度更新有两大优势：

对于不相似的点，用一个较小的距离会产生较大的梯度来让这些点排斥开来。

这种排斥又不会无限大（梯度中分母） ，避免不相似的点距离太远。

2.4 算法过程

Data: X=x1,....xn

计算cost function 的参数

优化参数： 设置迭代次数T，学习速率n，动量

目标结果是低维数据表示，YT=y1,...,yn 

开始优化：

计算给定Perp 下的条件概率，pj|i

令pij=(pj|i +pi|j)/2n

用N(0,10-4I) 随机初始化Y

迭代，从t=1 到T，做如下的操作:

      计算低维度下的qij ，计算梯度，更新Yt

结束

我们对比一下高斯分布和t分布(如上图,code见probability/distribution.md), t分布受异常值影响更小，拟合结果更为合理，较好的捕获了数据的整体特征。

使用了t分布之后的q变化，如下:

                                                                     q_{ij} = \frac{(1 + \mid \mid y_i -y_j \mid \mid ^2)^{-1}}{\sum_{k \neq l} (1 + \mid \mid y_i -y_j \mid \mid ^2)^{-1}}

此外，t分布是无限多个高斯分布的叠加，计算上不是指数的，会方便很多。优化的梯度如下:

                                                               \frac{\delta C}{\delta y_i} = 4 \sum_j(p_{ij}-q_{ij})(y_i-y_j)(1+ \mid \mid y_i-y_j \mid \mid ^2)^{-1}

t-sne的有效性，也可以从上图中看到：横轴表示距离，纵轴表示相似度, 可以看到，对于较大相似度的点，t分布在低维空间中的距离需要稍小一点；而对于低相似度的点，t分布在低维空间中的距离需要更远。这恰好满足了我们的需求，即同一簇内的点(距离较近)聚合的更紧密，不同簇之间的点(距离较远)更加疏远。

总结一下，t-SNE的梯度更新有两大优势：

  • 对于不相似的点，用一个较小的距离会产生较大的梯度来让这些点排斥开来。
  • 这种排斥又不会无限大(梯度中分母)，避免不相似的点距离太远。

2.5 不足

1 主要用于可视化，

2 倾向与保存局部特征

3 没有唯一最优解

4 训练很慢

更详细的介绍:https://blog.csdn.net/scott198510/article/details/76099700

对kl散度的介绍如下

 1 KL散度、JS散度和交叉熵
 2 三者都是用来衡量两个概率分布之间的差异性的指标。不同之处在于它们的数学表达。
 3 对于概率分布P(x)和Q(x)
 4 1）KL散度（Kullback–Leibler divergence）
 5 又称KL距离，相对熵。
 6 
 7 当P(x)和Q(x)的相似度越高，KL散度越小。
 8 KL散度主要有两个性质：
 9 （1）不对称性
10 尽管KL散度从直观上是个度量或距离函数，但它并不是一个真正的度量或者距离，因为它不具有对称性，即D(P||Q)!=D(Q||P)。
11 （2）非负性
12 相对熵的值是非负值，即D(P||Q)>0。
13  
14 2）JS散度（Jensen-Shannon divergence）
15 JS散度也称JS距离，是KL散度的一种变形。
16 
17 但是不同于KL主要又两方面：
18 （1）值域范围
19 JS散度的值域范围是[0,1]，相同则是0，相反为1。相较于KL，对相似度的判别更确切了。
20 （2）对称性
21 即 JS(P||Q)=JS(Q||P)，从数学表达式中就可以看出。
22 3）交叉熵（Cross Entropy）
23 在神经网络中，交叉熵可以作为损失函数，因为它可以衡量P和Q的相似性。
24 
25 交叉熵和相对熵的关系：
26 
27 以上都是基于离散分布的概率，如果是连续的数据，则需要对数据进行Probability Density Estimate来确定数据的概率分布，就不是求和而是通过求积分的形式进行计算了。
28  
29 个人理解：
30 1、KL散度本质是用来衡量两个概率分布的差异一种数学计算方式；由于用到比值除法不具备对称性；
31 2、神经网络训练时为何不用KL散度，从数学上来讲，它们的差异在于KL散度多减了一个 H(P)；P代表真实分布，Q代表估计的分布
32 
33 从损失函数角度来看，在训练样本固定的情况下，H(P)是个常数，对梯度更新没有价值；所以两者的最优解是一样的；

 

posted @ 2020-08-13 21:44  你的雷哥  阅读(1004)  评论(0)  编辑  收藏  举报