正定矩阵和半正定矩阵

在众多的机器学习模型中，线性代数的身影无处不在，当然，我们也会时常碰到线性代数中的正定矩阵和半正定矩阵。例如，多元正态分布的协方差矩阵要求是半正定的。

--------------×--------------×--------------

1. 基本的定义

正定和半正定这两个词的英文分别是positive definite和positive semi-definite，其中，definite是一个形容词，表示“明确的、确定的”等意思。

初学线性代数的读者可能会被这两个词“唬住”，但正定矩阵和半正定矩阵的定义实际上是很简单的 (不考虑复数构成的矩阵)：

【定义1】给定一个大小为 $n\times n$ 的实对称矩阵 $A$ ，若对于任意长度为 $n$ 的非零向量 $\boldsymbol{x}$ ，有 $\boldsymbol{x}^TA\boldsymbol{x}>0$ 恒成立，则矩阵 $A$ 是一个正定矩阵。

【例1】单位矩阵 $I\in\mathbb{R}^{2\times 2}$ 是否是正定矩阵？

解：设向量 $\boldsymbol{x}=\left[ \begin{array}{c} x_1 \\ x_2 \\ \end{array} \right] \in\mathbb{R}^{2}$ 为非零向量，则

$\boldsymbol{x}^TI\boldsymbol{x}=\boldsymbol{x}^T\boldsymbol{x}=x_1^2+x_2^2$

由于 $\boldsymbol{x}\neq \boldsymbol{0}$ ，故 $\boldsymbol{x}^TI\boldsymbol{x}>0$ 恒成立，即单位矩阵 $I\in\mathbb{R}^{2\times 2}$ 是正定矩阵。

单位矩阵是正定矩阵 (positive definite)。

【简单证明】对于任意单位矩阵 $I\in\mathbb{R}^{n\times n}$ 而言，给定任意非零向量 $\boldsymbol{x}\in\mathbb{R}^{n}$ ，恒有

$\boldsymbol{x}^TI\boldsymbol{x}=\boldsymbol{x}^T\boldsymbol{x}$

$=x_1^2+x_2^2+\cdots+x_n^2>0$

【例2】实对称矩阵 $A=\left[ \begin{array}{ccc} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2 \\ \end{array} \right] \in\mathbb{R}^{3\times 3}$ 是否是正定矩阵？

解：设向量 $\boldsymbol{x}=\left[ \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \end{array} \right] \in\mathbb{R}^{3}$ 为非零向量，则

$\boldsymbol{x}^TA\boldsymbol{x}= \left[\begin{array}{ccc}(2x_1-x_2) & (-x_1+2x_2-x_3) & -x_2+2x_3\end{array}\right] \left[\begin{array}{c}x_1 \\ x_2 \\ x_3 \\ \end{array}\right]$

$=x_1^2+(x_1-x_2)^2+(x_2-x_3)^2+x_3^2>0$

因此，矩阵 $A$ 是正定矩阵。

【定义2】给定一个大小为 $n\times n$ 的实对称矩阵 $A$ ，若对于任意长度为 $n$ 的向量 $\boldsymbol{x}$ ，有 $\boldsymbol{x}^TA\boldsymbol{x}\geq0$ 恒成立，则矩阵 $A$ 是一个半正定矩阵。

根据正定矩阵和半正定矩阵的定义，我们也会发现：半正定矩阵包括了正定矩阵，与非负实数 (non-negative real number)和正实数 (positive real number)之间的关系很像。

图1 正实数与负实数，图片来源于https://en.wikipedia.org/wiki/Real_number

2. 从二次函数到正定/半正定矩阵

在初中数学中，我们学习了二次函数 $y=ax^2$ ，该函数的曲线会经过坐标原点，当参数 $a>0$ 时，曲线的“开口”向上，参数 $a<0$ 时，曲线的“开口”向下。

以 $y=2x^2$ 为例，曲线如下：

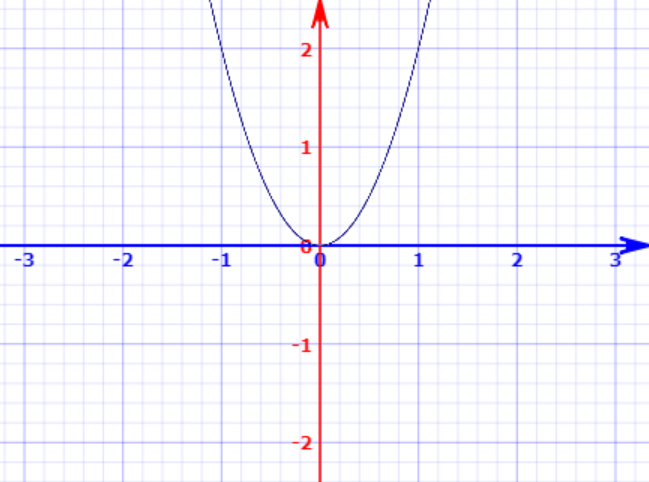图2 二次函数曲线

实际上，我们可以将 $y=\boldsymbol{x}^TA\boldsymbol{x}$ 视作 $y=ax^2$ 的多维表达式。

当我们希望 $y=\boldsymbol{x}^TA\boldsymbol{x}\geq0$ 对于任意向量 $\boldsymbol{x}$ 都恒成立，就要求矩阵 $A$ 是一个半正定矩阵，对应于二次函数， $y=ax^2>0,\forall x$ 需要使得 $a\geq0$ .

另外，在 $y=ax^2$ 中，我们还知道：若 $a>0$ ，则对于任意 $x\neq 0$ ，有 $y>0$ 恒成立。

这在 $y=\boldsymbol{x}^TA\boldsymbol{x}$ 也有契合之处，当矩阵 $A$ 是正定矩阵时，对于任意 $\boldsymbol{x}\neq \boldsymbol{0}$ ， $y>0$ 恒成立。

3. 正定矩阵和半正定矩阵的直观解释

若给定任意一个正定矩阵 $A\in\mathbb{R}^{n\times n}$ 和一个非零向量 $\boldsymbol{x}\in\mathbb{R}^{n}$ ，则两者相乘得到的向量 $\boldsymbol{y}=A\boldsymbol{x}\in\mathbb{R}^{n}$ 与向量 $\boldsymbol{x}$ 的夹角恒小于 $\frac{\pi}{2}$ . (等价于： $\boldsymbol{x}^TA\boldsymbol{x}>0$ .)

【例3】给定向量 $\boldsymbol{x}=\left[\begin{array}{c} 2 \\ 1 \\ \end{array} \right]\in\mathbb{R}^{2}$ ，对于单位矩阵 $I=\left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \\ \end{array}\right] \in\mathbb{R}^{2\times 2}$ ，则

$\boldsymbol{y}=I\boldsymbol{x}=\boldsymbol{x}=\left[\begin{array}{c} 2 \\ 1 \\ \end{array} \right]$

向量 $\boldsymbol{x},\boldsymbol{y}\in\mathbb{R}^{2}$ 之间的夹角为

$\cos\left<\boldsymbol{x},\boldsymbol{y}\right>=\frac{\boldsymbol{x}^T\boldsymbol{y}}{||\boldsymbol{x}||\cdot||\boldsymbol{y}||}$

$=\frac{2\times 2+1\times 1}{\sqrt{2^2+1^2}\cdot\sqrt{2^2+1^2}}$

$=1$

即两个向量之间的夹角为0°.

【例4】给定向量 $\boldsymbol{x}=\left[ \begin{array}{c} 1 \\ 2 \\ 1 \\ \end{array} \right] \in\mathbb{R}^{3}$ ，对于实对称矩阵 $A=\left[ \begin{array}{ccc} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2 \\ \end{array} \right] \in\mathbb{R}^{3\times 3}$ ，则

$\boldsymbol{y}=A\boldsymbol{x}= \left[ \begin{array}{c} 0 \\ 2 \\ 0 \\ \end{array} \right]$

向量 $\boldsymbol{x},\boldsymbol{y}\in\mathbb{R}^{2}$ 之间的夹角为

$\cos\left<\boldsymbol{x},\boldsymbol{y}\right>=\frac{\boldsymbol{x}^T\boldsymbol{y}}{||\boldsymbol{x}||\cdot||\boldsymbol{y}||}=\frac{\sqrt{6}}{3}$

即两个向量之间的夹角小于 $\frac{\pi}{2}$ .

若给定任意一个正定矩阵 $A\in\mathbb{R}^{n\times n}$ 和一个向量 $\boldsymbol{x}\in\mathbb{R}^{n}$ ，则两者相乘得到的向量 $\boldsymbol{y}=A\boldsymbol{x}\in\mathbb{R}^{n}$ 与向量 $\boldsymbol{x}$ 的夹角恒小于或等于 $\frac{\pi}{2}$ . (等价于： $\boldsymbol{x}^TA\boldsymbol{x}\geq0$ .)

4. 为什么协方差矩阵要是半正定的？

在概率论与数理统计中，我们都学习的协方差矩阵的定义：

对于任意多元随机变量 $\boldsymbol{t}$ ，协方差矩阵为
$C=\mathbb{E}\left[(\boldsymbol{t}-\bar{\boldsymbol{t}})(\boldsymbol{t}-\bar{\boldsymbol{t}})^T\right]$

现给定任意一个向量 $\boldsymbol{x}$ ，则

$\boldsymbol{x}^TC\boldsymbol{x}=\boldsymbol{x}^T\mathbb{E}\left[(\boldsymbol{t}-\bar{\boldsymbol{t}})(\boldsymbol{t}-\bar{\boldsymbol{t}})^T\right]\boldsymbol{x}$