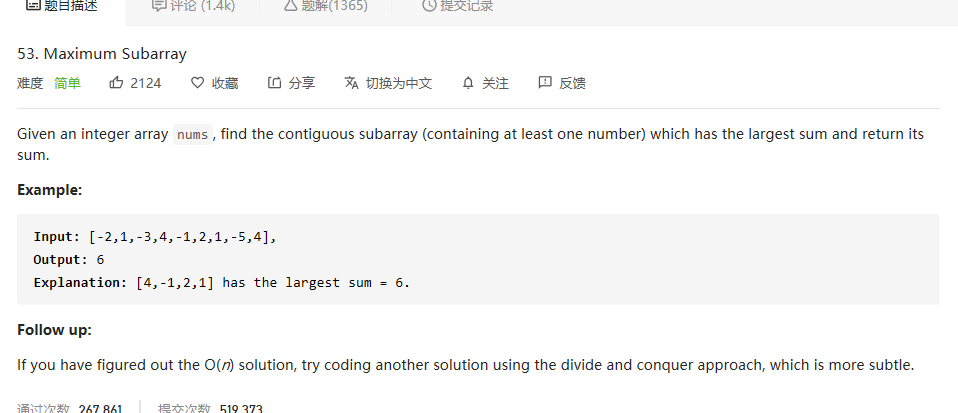
53. Maximum Subarr

题目链接

 

 

 思路一dp法：结果最后一个样例超时,说明还不够简化

class Solution:

    def maxSubArray(self,nums):
        lens = len(nums)
        sum = -10000000000000000
        maxsum = -1000000000000000
        p1 = p2 =0
        while True:
            sum = 0
            if p2 >= lens:
                break
            for i in range((p2-p1)+1):
                sum += nums[p1+i]
            if sum > maxsum:
                maxsum = sum
            if sum < 0:
                p1 = p2+1
                p2 = p1
            if sum >= 0:
                p2 = p2 + 1
        return maxsum


if __name__ == '__main__':
    nums = [-1,-2,0]
    print(Solution().maxSubArray(nums))

思路二：对思路一化简

这一段代码我运用了动态规划的思想，在此期间看了很多优秀，精简的算法，然后自己总结出来了这段代码
这段代码首先是一个迭代，从1到nums的最后一个数字(range这个函数不懂的可以查一下)，
然后就是总体了,nums[i]是从1开始的，开始算的是num[0]+nums[1]与nums[i]的最大值，
这里这么写可以看成nums[i-1]+nums[i]是看nums[i-1]大于0还是小于0，大于0自然选这个，
小于0的话，相加是要比num[i]小的，所以选择num[i]，这样一直往后迭代，最后返回max(nums),
也就是nums列表的最大值。

 

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        for i in range(1,len(nums)):
            nums[i] = max(nums[i-1]+nums[i],nums[i])
        return max(nums)