吴恩达《深度学习》第二门课(3)超参数调试、Batch正则化和程序框架
3.1调试处理
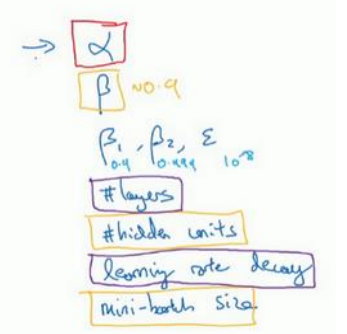
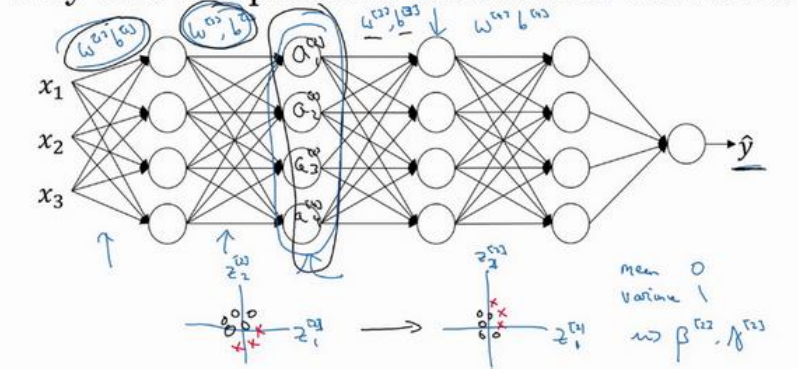
(1)不同超参数调试的优先级是不一样的,如下图中的一些超参数,首先最重要的应该是学习率α(红色圈出),然后是Momentum算法的β、隐藏层单元数、mini-batch size(黄色圈出)、再之后是Layer、learning rate decay(紫色圈出)、最后是Adam算法中的β1、β2、ε。
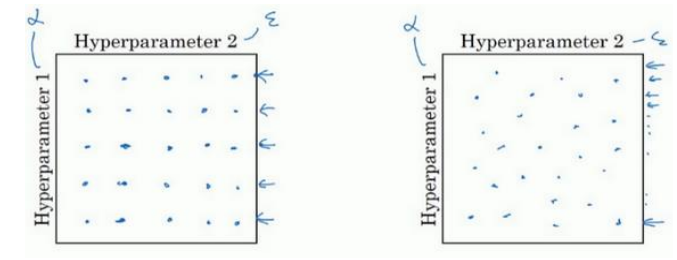
(2)用随机取值代替网格点取值。下图左边是网格点取值,如果二维参数中,一个参数调试的影响特别小,那么虽然取了25个点,其实只相当于取了5个不同的点;而右图中随机取值取了多少个点就代表有多少不同值的点。
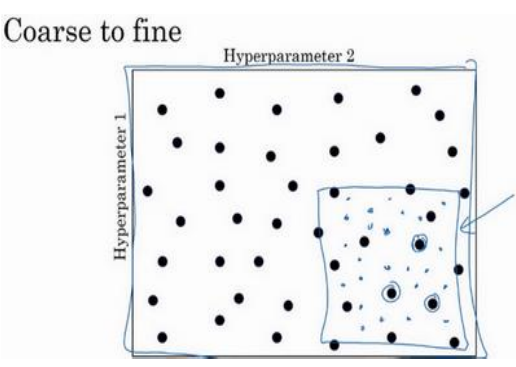
(3)由粗糙到精细的取值,先粗糙取值,然后发现最好的点,再在这个点附近进行精细的取值。如下图所示
3.2为超参数选择合适的范围
(1)随机取值并不是在取值范围内随机均匀取值,而是要选择合适的标尺来随机取值。
(2)案例1:在选择网络层数时,其范围是[2,4],那么直接均匀取值2,3,4都是合理的。
(3)案例2:如果在给学习率取值时,其范围是[0.0001,1],如果均匀取值,将会有90%的点落在0.1到1之间,这时不合理的;此时应该用对数坐标0.0001=10-4,1=100,所以应该是在[-4,0]上随机均匀取值作为r,然后10r作为学习率α。如下图所示

(4)指数加权平均的超参数β取值范围是[0.9,0.999],其方法是:1-β=[0.1,0.001],然后再根据学习率提到的用对数坐标来随机取值。
(5)在取值微小变化会带来巨大结果不同的地方(β在0.9990到0.9995敏感度就比0.9到0.9005高)即灵敏度高,需要去更多更密集的值,这就是为什么要选择合适的标尺。
3.3超参数训练的实践
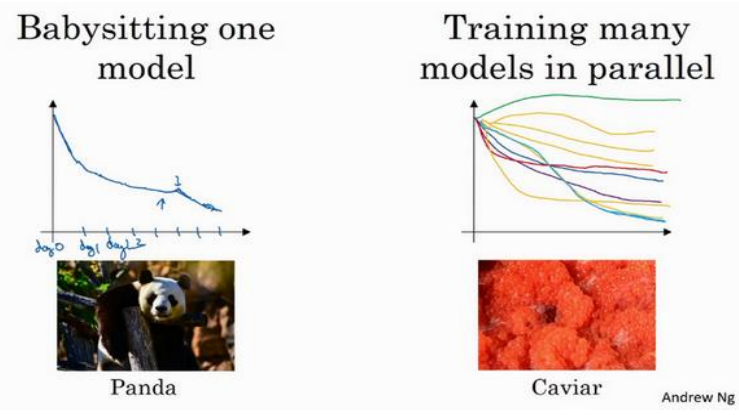
(1)当计算资源少的时候,只能一个模型慢慢调参,悉心照顾,当计算资源丰富时,可以模型同时选择不同参数进行训练,然后找出最优的。如下图所示
3.4归一化网络的激活函数
(1)计算过程如下图所示(总共包括四个式子):

(2)特征输入归一化之后均值为0,方差为1,但是对隐藏层的归一化而言,她的均值和方差是空调的,即通过γ、β两个超参数调整。之所以不希望都是均值为0,方差为1,因为那样的话可能都集中再激活函数的线性区域,导致可能没法得到任意想要的值。如下图所示
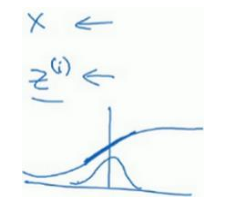
(3)一般情况下都是对z(即激活函数之前)进行归一化的。
这篇博客更详细介绍了batch归一化的内容:透彻分析批归一化Batch Normalization强大作用
3.5将Batch Norm拟合进神经网络
(1)使用以下公式来进行更新参数,其中原来的b已经可以去掉,因为不管是多少都会在归一化中被消除,然后用新的参数β替代(此处的β是归一化时的参数,不是优化算法中的β):
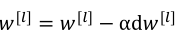
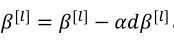
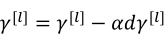
除了以上的这种更新方式之外,也可以用其他优化算法进行更新。
3.6Batch Norm为什么奏效
(1)浅层的理解可以按照之前提到的,把输入特征归一化之后,可以加快训练的思路来理解每一层归一化的作用。
(2)深层原因:当已经学的x到y的映射,然后当x的分布发生变化是,该映射将需要重新学习,这里的x可以理解成中间的某一隐藏层,x的分布是受到它前面层参数的影响的,为了时x的分布尽量不受到影响(这样x到y的映射可以尽量少做调整),所以加入了归一化,这样x的均值可以始终固定为β,方差固定为α。这样即使x值会发生变化,但是其分布是不变的(或者说变得更少),这样一来减弱了前层参数对后层参数的影响,互相之间相对较独立,更有利于各层之间学习自己的映射,这样有助于加速网络的训练。如下图中框选出来的中间层它的值受前面参数影响,同时又是后层的输入,归一化保证了该层的分布不变性。
3.7测试时的Batch Norm
(1)训练时mini-batch有样本来计算均值和方差,如下式子(式子中的m是mini-batch size):
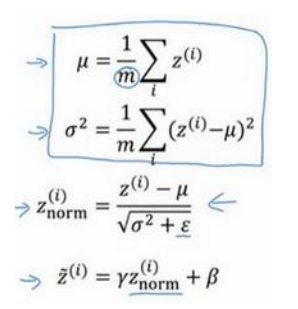
(2)但是在测试集时,是一个一个进行测试的,一个样本求均值和方差是没有意义的。所以使用的到方法就是:在训练是每一个批次获得对应的均值和方差,然后用之前提到的指数加权平均来实时获得最新的均值和方差给测试时来用(当然还有其他估算均值和方差的方法)。有了均值和方差之后,测试数据就可以按照上面的式子进行归一化了,使用的β、γ是训练出来的。
batch_normalization是设计用来解决网络层加深而导致的梯度弥散问题,一般都是加到卷积层的后面的;L2正则化的话可以加到任何层,如果你觉得某一层的参数会变得很大,可以加一个,可以避免过拟合。
3.8Softmax回归
(1)softmax激活函数常用于多分类问题的最后一层作为激活函数,它将最后一层算出来的z[L]取幂函数,然后求和,最后再把每个单元取幂函数之后都分别除以求和,得到各自的概率输出。如下所示
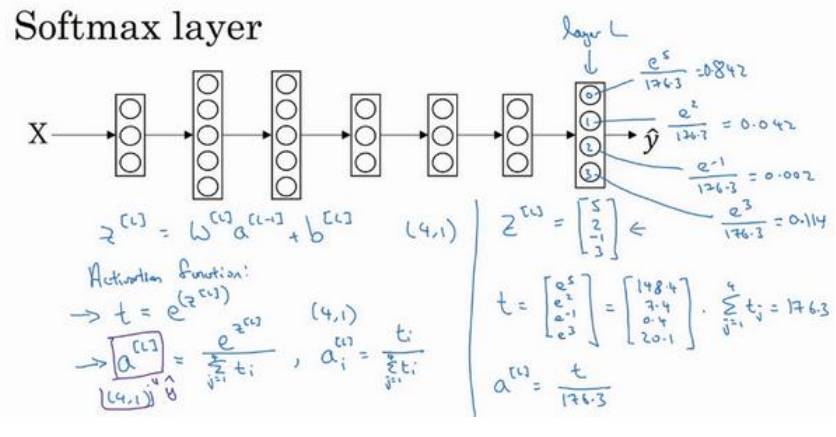
3.9训练一个Softmax分类器
(1)分类器的损失函数(一个样本):
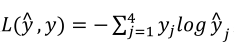
如四分类器中样本标签(左边)和预测值(右边)如下:
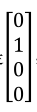 ,
,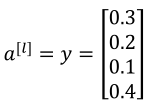
所以损失函数简化为:

(2)代价函数:

3.10深度学习框架
(1)一些常见的深度学习框架

3.11TensorFlow
(1)给一个TensorFlow的简单使用案例:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号