吴恩达《深度学习》第二门课（2）优化算法
2.1Mini-batch梯度下降
（1）例如有500万个训练样本，这时可以每1000个组成一个Mini-batch,共用5000个Mini-batch。主要是为了加快训练。
（2）循环完所有的训练样本称为（1 epoch）。
（3）使用大括号X{t},Y{t}表示一个Mini-batch。（小括号（i）表示第i个样本，中括号[l]表示神经网络第l层）。
2.2理解mini-batch梯度下降法
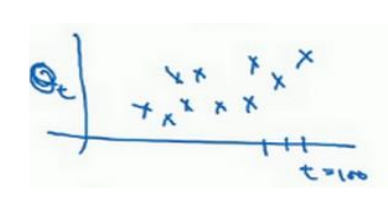
（1）batch梯度下降时，每一次迭代代价函数都会降低（如果某一次不是，说明出问题了，可能要改变学习率），而mini-batch梯度下降时，不一定每次都降低，但是总的趋势是下降的。如下图所示：
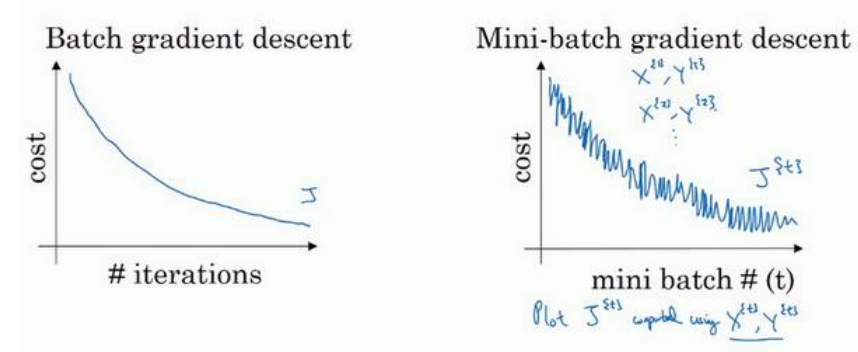
（2）Mini-batch的大小设为m（总样本数）时，变成了batch梯度下降（训练慢当样本总数大时），当设为1，变成了随机梯度下降（这时没能很好利用多样本的向量化的优势，也会导致变慢）。所示实际中选择不大不小的mini-batch尺寸，下降速度达到最快。
（3）不管是随机梯度下降还是mini-batch梯度下降都不会达到收敛，如下图所示紫色线条，所以后期需要减小学习率来使其趋向收敛。
（4）当样本数小于2000时可直接使用batch梯度下降，当样本数很大时，一般把mini-batch的大小设为2的n次方，比如64,126,512等，这样是考虑到电脑内存设置和使用方法。
（5）同第四点，所以在调参mini-batch的大小时常常设置2的不同次方。
min_batch梯度下降算法和随机梯度下降算法和批量梯度下降算法的比较（总的来说就是随机梯度下降算法没有用到向量计算的加速优势，batch梯度下降算法每次迭代更新都要遍历计算所有的数据，因此计算量大，占CPU，而minibatch刚好中和解决了这两个缺点）
2.3指数加权平均数
（1）下图中蓝色为每天的的温度，红色是温度的指数加权平均数，使用如下公式计算而来：
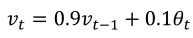
（2）将上式更一般的表示如下：
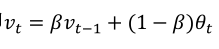
β越大，反应越快，波动性却强，如下图中黄色线；β越小，延迟多大，越平缓，如下图中绿色线。
（3）在计算时，可以认为vt是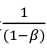
天的平均温度，如β等于0.5时，看成是两天的平均温度，β=0.98，则是50天的平均温度。因此B值决定了曲线的波动情况，B值越大，曲线越平滑，历史天气决定性大，不能实时适应天气突变。而B越小则曲线变化的越大，
2.4理解指数加权平均数
（1）根据下面式子：
进行展开：
所以V100其实是下面两个图对应点乘积的求和（右图是从0.1开始往左指数下降）：
（2）当β为0.9时，下降到第十天（0.9）10约等于0.35，大约是1/e,认为降到这个数之后可以忽略不计了。
（3）指数加权平均数公式的好处之一就在于，他占用极少内存，电脑内存中占用一行数字而已，然后把最新的数据代入公式，不断覆盖就可以了。
2.5指数加权平均数的偏差修正
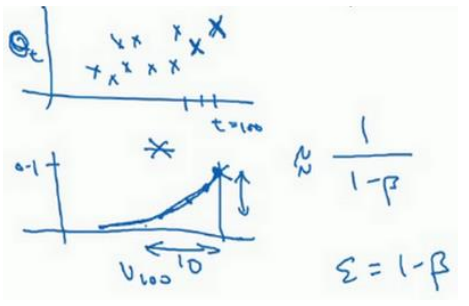
（1）按照前面提到的公式计算，比如β为0.9，得不到下图中绿色的线，而是得到紫色的线，因为一开始已经没有之前的数据可以加了，导致小了很多。
（2）解决方法是引入偏差修正，即按照之前的公式算出vt之后，再除以（1-βt）,如下所示：
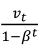
当t=2时：
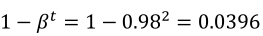
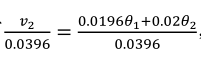
这样将能能到绿色的线，当t很大时，分母也趋向于1，那时将不起作用（也不需要起作用）。
如上图紫色线在开始时低于绿色线，之后重合，原因是v0 = 0.所以之后v1根据公式变小，因此影响到前期的曲线，所以有必要进行修正，但是如果你不关心前期数据可以不进行修正。
2.6动量梯度下降法（Momentum）
（1）下图中蓝色是梯度下降的过程：是不断抖动的
使用了带动量的梯度下降，由于梯度的计算使用了指数加权平均方法，使得本次梯度的计算和之前是有关联的，这样就能抵消比如梯度在上下摆动的这种状况，而真正的下降方向（朝右边走）却能很好保持，这样使得收敛优化变得更快
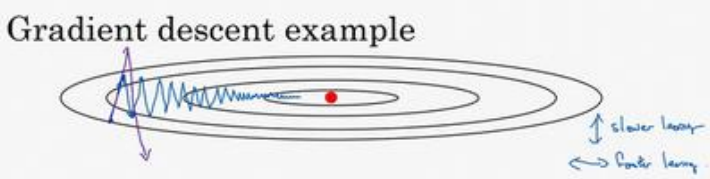
（2）我们希望沿着垂直方向的振幅能变小，因为是无效的，同时因为振幅的存在使得学习率不能太大，太大振幅会更大，甚至训练的越来越差；同时横轴方向希望学习率能增大，更加快速的到达最优点，以上矛盾的两者，可以通过上一节讲到的指数加权平均来解决（因为垂直方向的均值为0，通过加权平均之后将会减小或者消除振幅，横轴方向因为始终吵着一个方向，所以进行指数加权平均没多大影响），公式如下：
（3）是否进行偏差修正影响不大，β取0.9是一个比较好的参数，学习率α会随之β的修改做一定的修改。
然而网上更多的是另外一种版本，即去掉（1-β），相当于上一版本上本次梯度的影响权值*1/(1-β) ，两者效果相当，只不过会影响一些最优学习率的选取
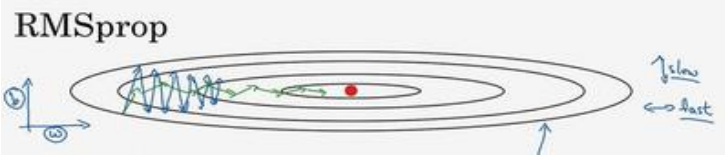
2.7RMSprop
（1）下图中，沿着b振幅大，说明db比较大：
（2）使用如下式子进行参数更新，理解：前两个式子平方之后将不会出现Momentum中权值平均后变为0的情况，哪边振幅大对应计算结果大，所以Sdw较小，Sdb较大；然后dw除以一个较小的数也就相当于取了较大的学习率，db除了一个较大的数，也就相当于取了一个较小的学习率，这就是RMSprop：
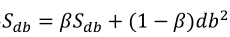
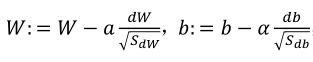
（3）最终会按照绿色的线优化：
2.8Adam 优化算法
（1）按照下列式子顺序即可得到Adam,他完美的讲上面提到的两种算法结合在了一起，需要注意一点是，Adam需要参数修正：
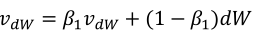
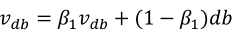
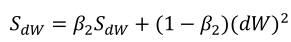
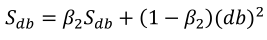
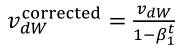
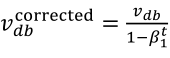
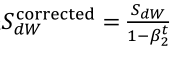
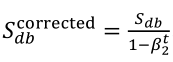
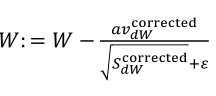
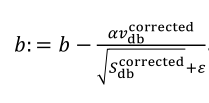
（2）参数涉及学习率α，β1（Momentum），β2（RMSprop）,ε（RMSprop）,其中学习率需要调整，其他三个参数使用下面图中的默认值就很好。
2.9学习率衰减（Learning rate decay）
（1）以下公式是一个学习率衰减的式子，其中包含了初始学习率a0好衰减率（decay-rate）两个参数需要调整：
（2）其他降低学习率的式子：
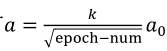
（3）还有离散的学习率，过一会变成原来的一半，还有不少人直接手动调整。
2.10局部最优的问题
（1）在低维（如二维）可能陷入局部最优，如下图：
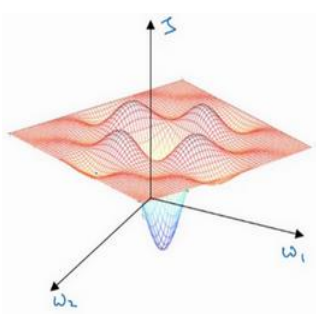
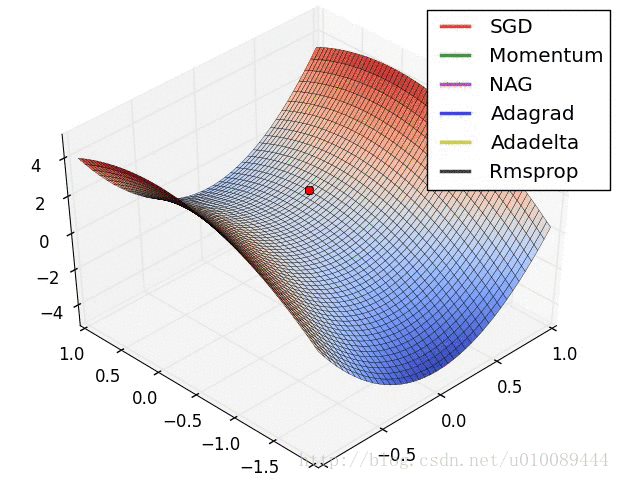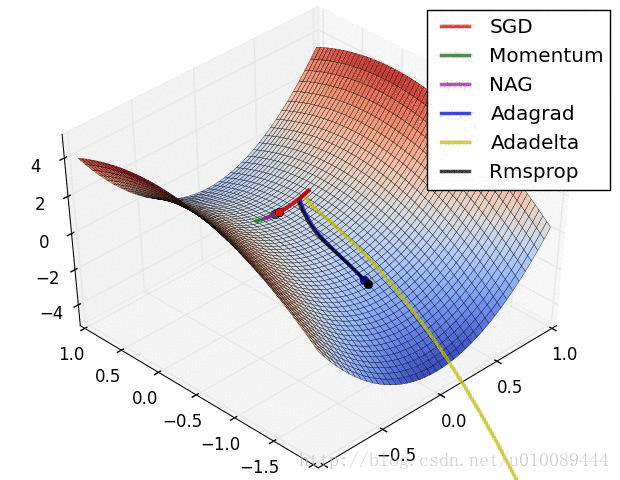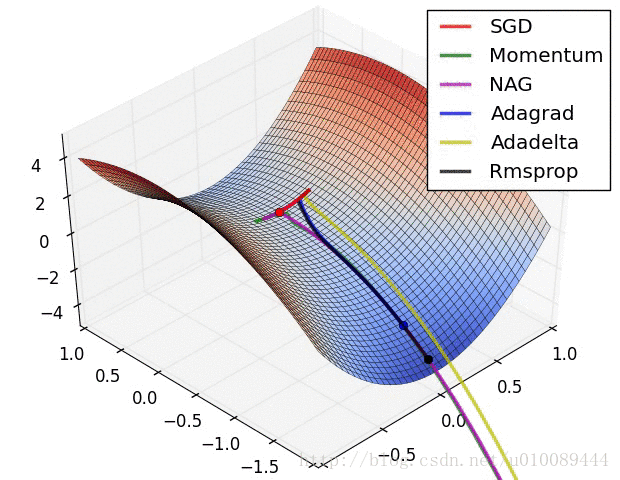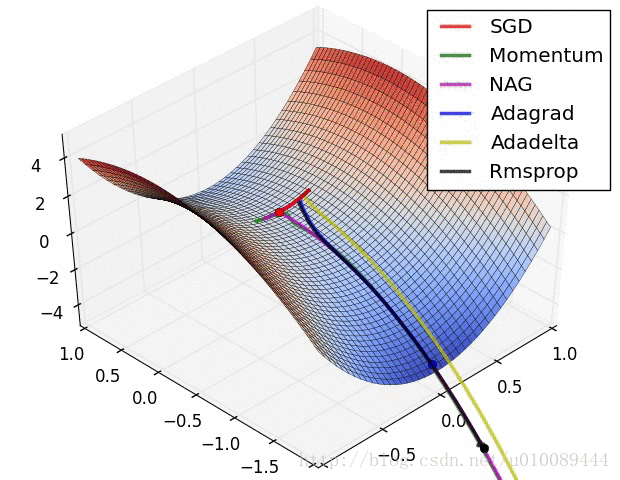
（2）但是在高维中，比如20000维，陷入局部最优的概率是2-20000（即每一维度都梯度为零，几乎不可能），所以更多的时候是出现处在鞍点上：如下图：
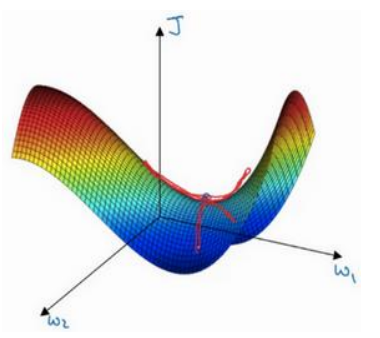
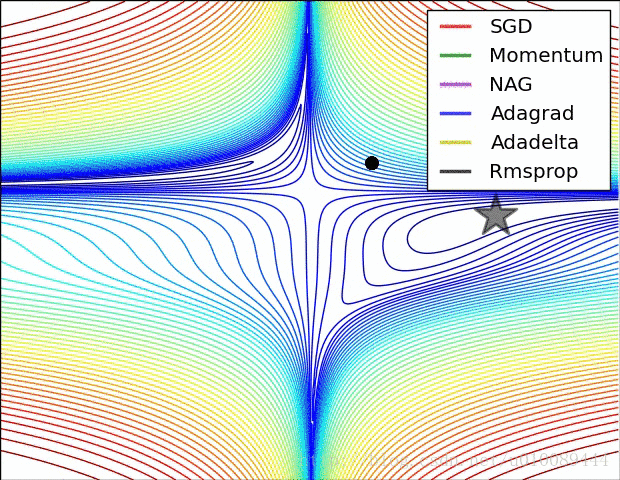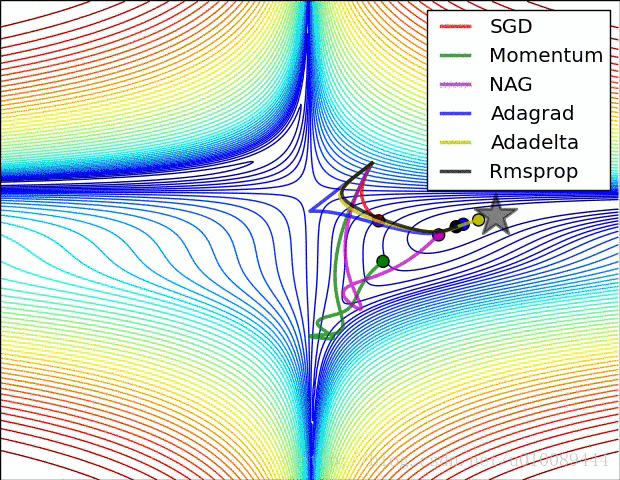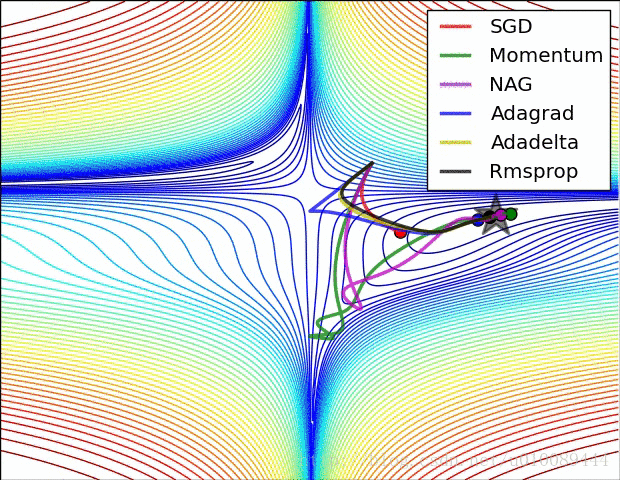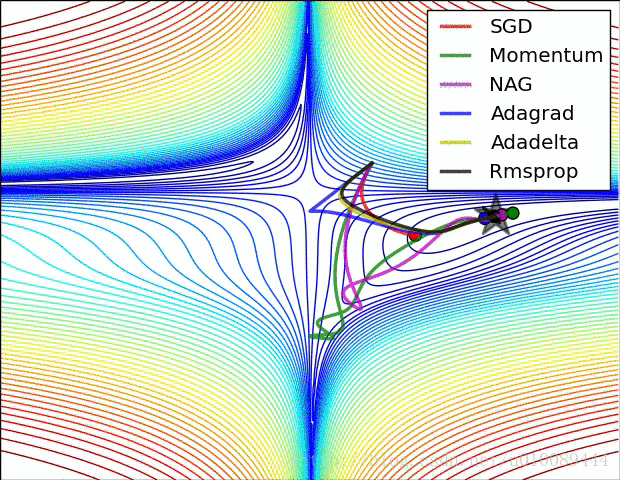
（3）存在的问题是：在平稳端学习缓慢，上面提到的算法如Adam,能够更快的走出平稳区。
