支持向量机SVM
svm简介
当训练样本近似线性可分时，通过软间隔最大化，学习一个线性支持向量机；
当训练样本线性不可分时，通过核技巧和软间隔最大化，学习一个非线性支持向量机；
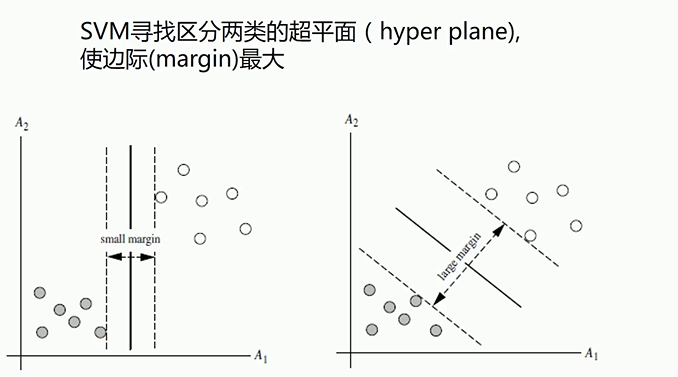
如果一个线性函数能够将样本分开，称这些数据样本是线性可分的。那么什么是线性函数呢？其实很简单，在二维空间中就是一条直线，在三维空间中就是一个平面，以此类推，如果不考虑空间维数，
1 from sklearn import svm 2 x = [[3, 3], [4, 3], [1, 1]] 3 y = [1, 1, -1] 4 5 model = svm.SVC(kernel='linear') 6 model.fit(x,y) 7 print(model.support_vectors_)# 打印支持向量 8 print(model.support_)# 打印是支持向量的样本点的下标[2 0] 9 print(model.n_support_)## 有几个支持向量[1 1],两个1说明两个支持向量[3, 3]，[1, 1] 10 print(model.predict([[4,3]]))#[1] 11 print(model.coef_)#参数 12 print(model.intercept_)#截距
1 import numpy as np 2 import matplotlib.pyplot as plt 3 from sklearn import svm 4 # 创建40个点 5 x_data = np.r_[np.random.randn(20, 2) - [2, 2], np.random.randn(20, 2) + [2, 2]] 6 y_data = [0]*20 +[1]*20 7 plt.scatter(x_data[:,0],x_data[:,1],c=y_data) 8 plt.show() 9 #fit the model 10 model = svm.SVC(kernel='linear') 11 model.fit(x_data, y_data) 12 model.coef_ 13 model.intercept_ 14 # 获取分离平面 15 16 plt.scatter(x_data[:,0],x_data[:,1],c=y_data) 17 x_test = np.array([[-5],[5]]) 18 d = -model.intercept_/model.coef_[0][1]#x1*w1+x2*w2+b=0此时把x2看为y即可 19 k = -model.coef_[0][0]/model.coef_[0][1] 20 y_test = d + k*x_test 21 plt.plot(x_test, y_test, 'k')#黑色线 22 plt.show() 23 model.support_vectors_ 24 # 画出通过支持向量的分界线 25 b1 = model.support_vectors_[0] 26 print(b1) 27 y_down = k*x_test + (b1[1] - k*b1[0]) 28 b2 = model.support_vectors_[-1] 29 y_up = k*x_test + (b2[1] - k*b2[0]) 30 plt.scatter(x_data[:,0],x_data[:,1],c=y_data) 31 x_test = np.array([[-5],[5]]) 32 d = -model.intercept_/model.coef_[0][1] 33 k = -model.coef_[0][0]/model.coef_[0][1] 34 y_test = d + k*x_test 35 plt.plot(x_test, y_test, 'k') 36 plt.plot(x_test, y_down, 'r--') 37 plt.plot(x_test, y_up, 'b--') 38 plt.show()
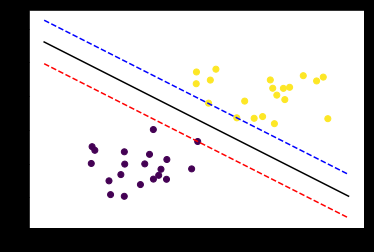
SVM核函数
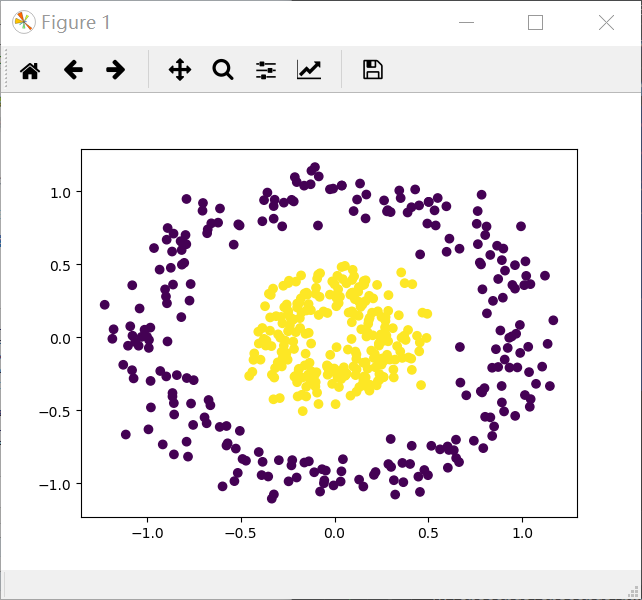
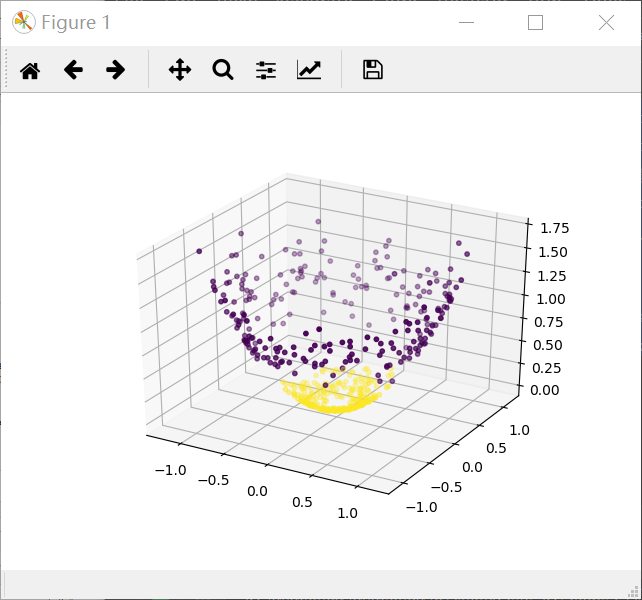
对于非线性的分类，我们可以使用SVM实现低维到高维的映射，寻找超平面之后再映射到低纬，但计算复杂度很高，我们可以使用核函数实现相同功能，但复杂度很低
1 import matplotlib.pyplot as plt 2 from sklearn import datasets 3 from mpl_toolkits.mplot3d import Axes3D 4 x_data, y_data = datasets.make_circles(n_samples=500,factor=.3,noise=.10) 5 plt.scatter(x_data[:,0],x_data[:,1],c=y_data) 6 plt.show() 7 z_data = x_data[:,0]**2 + x_data[:,1]**2 8 ax = plt.figure().add_subplot(111,projection = '3d') 9 ax.scatter(x_data[:,0],x_data[:,1],z_data,c= y_data,s=10) 10 plt.show()
LR-testSet2.txt
1 0.051267,0.69956,1 2 -0.092742,0.68494,1 3 -0.21371,0.69225,1 4 -0.375,0.50219,1 5 -0.51325,0.46564,1 6 -0.52477,0.2098,1 7 -0.39804,0.034357,1 8 -0.30588,-0.19225,1 9 0.016705,-0.40424,1 10 0.13191,-0.51389,1 11 0.38537,-0.56506,1 12 0.52938,-0.5212,1 13 0.63882,-0.24342,1 14 0.73675,-0.18494,1 15 0.54666,0.48757,1 16 0.322,0.5826,1 17 0.16647,0.53874,1 18 -0.046659,0.81652,1 19 -0.17339,0.69956,1 20 -0.47869,0.63377,1 21 -0.60541,0.59722,1 22 -0.62846,0.33406,1 23 -0.59389,0.005117,1 24 -0.42108,-0.27266,1 25 -0.11578,-0.39693,1 26 0.20104,-0.60161,1 27 0.46601,-0.53582,1 28 0.67339,-0.53582,1 29 -0.13882,0.54605,1 30 -0.29435,0.77997,1 31 -0.26555,0.96272,1 32 -0.16187,0.8019,1 33 -0.17339,0.64839,1 34 -0.28283,0.47295,1 35 -0.36348,0.31213,1 36 -0.30012,0.027047,1 37 -0.23675,-0.21418,1 38 -0.06394,-0.18494,1 39 0.062788,-0.16301,1 40 0.22984,-0.41155,1 41 0.2932,-0.2288,1 42 0.48329,-0.18494,1 43 0.64459,-0.14108,1 44 0.46025,0.012427,1 45 0.6273,0.15863,1 46 0.57546,0.26827,1 47 0.72523,0.44371,1 48 0.22408,0.52412,1 49 0.44297,0.67032,1 50 0.322,0.69225,1 51 0.13767,0.57529,1 52 -0.0063364,0.39985,1 53 -0.092742,0.55336,1 54 -0.20795,0.35599,1 55 -0.20795,0.17325,1 56 -0.43836,0.21711,1 57 -0.21947,-0.016813,1 58 -0.13882,-0.27266,1 59 0.18376,0.93348,0 60 0.22408,0.77997,0 61 0.29896,0.61915,0 62 0.50634,0.75804,0 63 0.61578,0.7288,0 64 0.60426,0.59722,0 65 0.76555,0.50219,0 66 0.92684,0.3633,0 67 0.82316,0.27558,0 68 0.96141,0.085526,0 69 0.93836,0.012427,0 70 0.86348,-0.082602,0 71 0.89804,-0.20687,0 72 0.85196,-0.36769,0 73 0.82892,-0.5212,0 74 0.79435,-0.55775,0 75 0.59274,-0.7405,0 76 0.51786,-0.5943,0 77 0.46601,-0.41886,0 78 0.35081,-0.57968,0 79 0.28744,-0.76974,0 80 0.085829,-0.75512,0 81 0.14919,-0.57968,0 82 -0.13306,-0.4481,0 83 -0.40956,-0.41155,0 84 -0.39228,-0.25804,0 85 -0.74366,-0.25804,0 86 -0.69758,0.041667,0 87 -0.75518,0.2902,0 88 -0.69758,0.68494,0 89 -0.4038,0.70687,0 90 -0.38076,0.91886,0 91 -0.50749,0.90424,0 92 -0.54781,0.70687,0 93 0.10311,0.77997,0 94 0.057028,0.91886,0 95 -0.10426,0.99196,0 96 -0.081221,1.1089,0 97 0.28744,1.087,0 98 0.39689,0.82383,0 99 0.63882,0.88962,0 100 0.82316,0.66301,0 101 0.67339,0.64108,0 102 1.0709,0.10015,0 103 -0.046659,-0.57968,0 104 -0.23675,-0.63816,0 105 -0.15035,-0.36769,0 106 -0.49021,-0.3019,0 107 -0.46717,-0.13377,0 108 -0.28859,-0.060673,0 109 -0.61118,-0.067982,0 110 -0.66302,-0.21418,0 111 -0.59965,-0.41886,0 112 -0.72638,-0.082602,0 113 -0.83007,0.31213,0 114 -0.72062,0.53874,0 115 -0.59389,0.49488,0 116 -0.48445,0.99927,0 117 -0.0063364,0.99927,0 118 0.63265,-0.030612,0
1 import matplotlib.pyplot as plt 2 import numpy as np 3 from sklearn.metrics import classification_report 4 from sklearn import svm 5 # 载入数据 6 data = np.genfromtxt("LR-testSet2.txt", delimiter=",") 7 x_data = data[:, :-1] 8 y_data = data[:, -1] 9 def plot(): 10 x0 = [] 11 x1 = [] 12 y0 = [] 13 y1 = [] 14 # 切分不同类别的数据 15 for i in range(len(x_data)): 16 if y_data[i] == 0: 17 x0.append(x_data[i, 0]) 18 y0.append(x_data[i, 1]) 19 else: 20 x1.append(x_data[i, 0]) 21 y1.append(x_data[i, 1]) 22 23 # 画图 24 scatter0 = plt.scatter(x0, y0, c='b', marker='o') 25 scatter1 = plt.scatter(x1, y1, c='r', marker='x') 26 # 画图例 27 plt.legend(handles=[scatter0, scatter1], labels=['label0', 'label1'], loc='best') 28 29 30 plot() 31 plt.show() 32 # fit the model 33 # C和gamma 34 model = svm.SVC(kernel='rbf') 35 model.fit(x_data, y_data) 36 print(model.score(x_data,y_data)) 37 # 获取数据值所在的范围 38 x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1 39 y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1 40 # 生成网格矩阵 41 xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), 42 np.arange(y_min, y_max, 0.02)) 43 44 z = model.predict(np.c_[xx.ravel(), yy.ravel()])# ravel与flatten类似，多维数据转一维。flatten不会改变原始数据，ravel会改变原始数据 45 z = z.reshape(xx.shape) 46 # 等高线图 47 cs = plt.contourf(xx, yy, z) 48 plot() 49 plt.show()
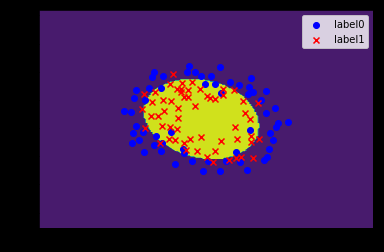
SVM松弛变量和惩罚函数
1.松弛变量
现在我们已经把一个本来线性不可分的文本分类问题，通过映射到高维空间而变成了线性可分的。就像下图这样：
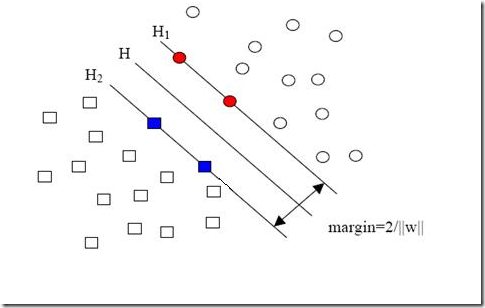
圆形和方形的点各有成千上万个（毕竟，这就是我们训练集中文档的数量嘛，当然很大了）。现在想象我们有另一个训练集，只比原先这个训练集多了一篇文章，映射到高维空间以后（当然，也使用了相同的核函数），也就多了一个样本点，但是这个样本的位置是这样的：
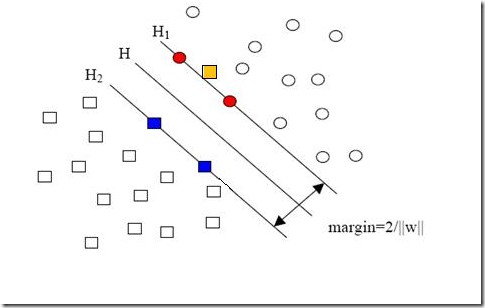
就是图中黄色那个点，它是方形的，因而它是负类的一个样本，这单独的一个样本，使得原本线性可分的问题变成了线性不可分的。这样类似的问题（仅有少数点线性不可分）叫做“近似线性可分”的问题。
以我们人类的常识来判断，说有一万个点都符合某种规律（因而线性可分），有一个点不符合，那这一个点是否就代表了分类规则中我们没有考虑到的方面呢（因而规则应该为它而做出修改）？
其实我们会觉得，更有可能的是，这个样本点压根就是错误，是噪声，是提供训练集的同学人工分类时一打瞌睡错放进去的。所以我们会简单的忽略这个样本点，仍然使用原来的分类器，其效果丝毫不受影响。
但这种对噪声的容错性是人的思维带来的，我们的程序可没有。由于我们原本的优化问题的表达式中，确实要考虑所有的样本点（不能忽略某一个，因为程序它怎么知道该忽略哪一个呢？），在此基础上寻找正负类之间的最大几何间隔，而几何间隔本身代表的是距离，是非负的，像上面这种有噪声的情况会使得整个问题无解。这种解法其实也叫做“硬间隔”分类法，因为他硬性的要求所有样本点都满足和分类平面间的距离必须大于某个值。
因此由上面的例子中也可以看出，硬间隔的分类法其结果容易受少数点的控制，这是很危险的（尽管有句话说真理总是掌握在少数人手中，但那不过是那一小撮人聊以自慰的词句罢了，咱还是得民主）。
但解决方法也很明显，就是仿照人的思路，允许一些点到分类平面的距离不满足原先的要求。由于不同的训练集各点的间距尺度不太一样，因此用间隔（而不是几何间隔）来衡量有利于我们表达形式的简洁。我们原先对样本点的要求是：
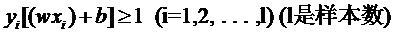
意思是说离分类面最近的样本点函数间隔也要比1大。如果要引入容错性，就给1这个硬性的阈值加一个松弛变量，即允许：
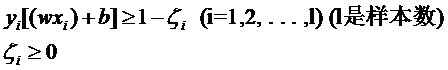
因为松弛变量是非负的，因此最终的结果是要求间隔可以比1小。但是当某些点出现这种间隔比1小的情况时（这些点也叫离群点），意味着我们放弃了对这些点的精确分类，而这对我们的分类器来说是种损失。但是放弃这些点也带来了好处，那就是使分类面不必向这些点的方向移动，因而可以得到更大的几何间隔（在低维空间看来，分类边界也更平滑）。显然我们必须权衡这种损失和好处。好处很明显，我们得到的分类间隔越大，好处就越多。回顾我们原始的硬间隔分类对应的优化问题：
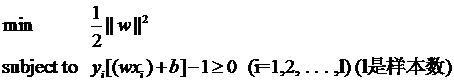
||w||^2就是我们的目标函数（当然系数可有可无），希望它越小越好，因而损失就必然是一个能使之变大的量（能使它变小就不叫损失了，我们本来就希望目标函数值越小越好）。那如何来衡量损失，有两种常用的方式，有人喜欢用：
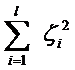
而有人喜欢用：
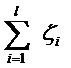
其中L都是样本的数目。两种方法没有大的区别。如果选择了第一种，得到的方法的就叫做二阶软间隔分类器，第二种就叫做一阶软间隔分类器。把损失加入到目标函数里的时候，就需要一个惩罚因子（cost，也就是libSVM的诸多参数中的C），原来的优化问题就变成了下面这样：
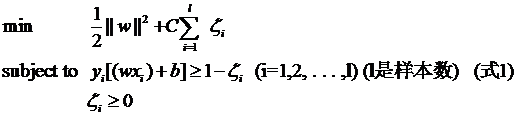
这个式子有这么几点要注意：
（1）并非所有的样本点都有一个松弛变量与其对应。实际上只有“离群点”才有，或者也可以这么看，所有没离群的点松弛变量都等于0（对负类来说，离群点就是在前面图中，跑到H2右侧的那些负样本点，对正类来说，就是跑到H1左侧的那些正样本点）。
（2）松弛变量的值实际上标示出了对应的点到底离群有多远，值越大，点就越远。
（3）惩罚因子C决定了你有多重视离群点带来的损失，显然当所有离群点的松弛变量的和一定时，你定的C越大，对目标函数的损失也越大，此时就暗示着你非常不愿意放弃这些离群点，最极端的情况是你把C定为无限大，这样只要稍有一个点离群，目标函数的值马上变成无限大，马上让问题变成无解，这就退化成了硬间隔问题。
（4）惩罚因子C不是一个变量，整个优化问题在解的时候，C是一个你必须事先指定的值，指定这个值以后，解一下，得到一个分类器，然后用测试数据看看结果怎么样，如果不够好，换一个C的值，再解一次优化问题，得到另一个分类器，再看看效果，如此就是一个参数寻优的过程，但这和优化问题本身决不是一回事，优化问题在解的过程中，C一直是定值，要记住。
（5）尽管加了松弛变量这么一说，但这个优化问题仍然是一个优化问题（汗，这不废话么），解它的过程比起原始的硬间隔问题来说，没有任何更加特殊的地方。
从大的方面说优化问题解的过程，就是先试着确定一下w，也就是确定了前面图中的三条直线，这时看看间隔有多大，又有多少点离群，把目标函数的值算一算，再换一组三条直线（你可以看到，分类的直线位置如果移动了，有些原来离群的点会变得不再离群，而有的本来不离群的点会变成离群点），再把目标函数的值算一算，如此往复（迭代），直到最终找到目标函数最小时的w。
啰嗦了这么多，读者一定可以马上自己总结出来，松弛变量也就是个解决线性不可分问题的方法罢了，但是回想一下，核函数的引入不也是为了解决线性不可分的问题么？为什么要为了一个问题使用两种方法呢？
其实两者还有微妙的不同。一般的过程应该是这样，还以文本分类为例。在原始的低维空间中，样本相当的不可分，无论你怎么找分类平面，总会有大量的离群点，此时用核函数向高维空间映射一下，虽然结果仍然是不可分的，但比原始空间里的要更加接近线性可分的状态（就是达到了近似线性可分的状态），此时再用松弛变量处理那些少数“冥顽不化”的离群点，就简单有效得多啦。
本节中的（式1）也确实是支持向量机最最常用的形式。至此一个比较完整的支持向量机框架就有了，简单说来，支持向量机就是使用了核函数的软间隔线性分类法。
2.惩罚因子
接下来要说的东西其实不是松弛变量本身，但由于是为了使用松弛变量才引入的，因此放在这里也算合适，那就是惩罚因子C。回头看一眼引入了松弛变量以后的优化问题：
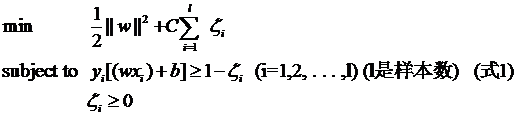
注意其中C的位置，也可以回想一下C所起的作用（表征你有多么重视离群点，C越大越重视，越不想丢掉它们）。这个式子是以前做SVM的人写的，大家也就这么用，但没有任何规定说必须对所有的松弛变量都使用同一个惩罚因子，我们完全可以给每一个离群点都使用不同的C，这时就意味着你对每个样本的重视程度都不一样，有些样本丢了也就丢了，错了也就错了，这些就给一个比较小的C；而有些样本很重要，决不能分类错误（比如中央下达的文件啥的，笑），就给一个很大的C。
当然实际使用的时候并没有这么极端，但一种很常用的变形可以用来解决分类问题中样本的“偏斜”问题。
先来说说样本的偏斜问题，也叫数据集偏斜（unbalanced），它指的是参与分类的两个类别（也可以指多个类别）样本数量差异很大。比如说正类有10，000个样本，而负类只给了100个，这会引起的问题显而易见，可以看看下面的图：
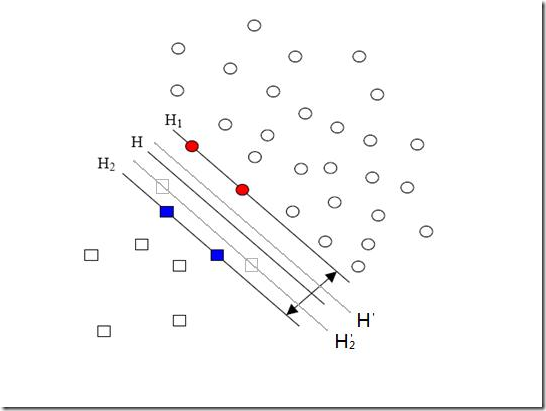
方形的点是负类。H，H1，H2是根据给的样本算出来的分类面，由于负类的样本很少很少，所以有一些本来是负类的样本点没有提供，比如图中两个灰色的方形点，如果这两个点有提供的话，那算出来的分类面应该是H’，H2’和H1，他们显然和之前的结果有出入，实际上负类给的样本点越多，就越容易出现在灰色点附近的点，我们算出的结果也就越接近于真实的分类面。但现在由于偏斜的现象存在，使得数量多的正类可以把分类面向负类的方向“推”，因而影响了结果的准确性。
对付数据集偏斜问题的方法之一就是在惩罚因子上作文章，想必大家也猜到了，那就是给样本数量少的负类更大的惩罚因子，表示我们重视这部分样本（本来数量就少，再抛弃一些，那人家负类还活不活了），因此我们的目标函数中因松弛变量而损失的部分就变成了：
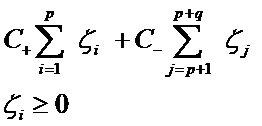
其中i=1…p都是正样本，j=p+1…p+q都是负样本。libSVM这个算法包在解决偏斜问题的时候用的就是这种方法。
那C+和C-怎么确定呢？它们的大小是试出来的（参数调优），但是他们的比例可以有些方法来确定。咱们先假定说C+是5这么大，那确定C-的一个很直观的方法就是使用两类样本数的比来算，对应到刚才举的例子，C-就可以定为500这么大（因为10，000：100=100：1嘛）。
但是这样并不够好，回看刚才的图，你会发现正类之所以可以“欺负”负类，其实并不是因为负类样本少，真实的原因是负类的样本分布的不够广（没扩充到负类本应该有的区域）。说一个具体点的例子，现在想给政治类和体育类的文章做分类，政治类文章很多，而体育类只提供了几篇关于篮球的文章，这时分类会明显偏向于政治类，如果要给体育类文章增加样本，但增加的样本仍然全都是关于篮球的（也就是说，没有足球，排球，赛车，游泳等等），那结果会怎样呢？虽然体育类文章在数量上可以达到与政治类一样多，但过于集中了，结果仍会偏向于政治类！所以给C+和C-确定比例更好的方法应该是衡量他们分布的程度。比如可以算算他们在空间中占据了多大的体积，例如给负类找一个超球——就是高维空间里的球啦——它可以包含所有负类的样本，再给正类找一个，比比两个球的半径，就可以大致确定分布的情况。显然半径大的分布就比较广，就给小一点的惩罚因子。
但是这样还不够好，因为有的类别样本确实很集中，这不是提供的样本数量多少的问题，这是类别本身的特征（就是某些话题涉及的面很窄，例如计算机类的文章就明显不如文化类的文章那么“天马行空”），这个时候即便超球的半径差异很大，也不应该赋予两个类别不同的惩罚因子。
看到这里读者一定疯了，因为说来说去，这岂不成了一个解决不了的问题？然而事实如此，完全的方法是没有的，根据需要，选择实现简单又合用的就好（例如libSVM就直接使用样本数量的比）。
SVM的应用
或许我们已经听到过，SVM在很多诸如文本分类，图像分类，生物序列分析和生物数据挖掘，手写字符识别等领域有很多的应用，但或许你并没强烈的意识到，SVM可以成功应用的领域远远超出现在已经在开发应用了的领域。
