Kmeans算法实现

 

 

 

 

下面的demo是根据kmeans算法原理实现的demo，使用到的数据是kmeans.txt

 1 1.658985 4.285136  
 2 -3.453687 3.424321  
 3 4.838138 -1.151539  
 4 -5.379713 -3.362104  
 5 0.972564 2.924086  
 6 -3.567919 1.531611  
 7 0.450614 -3.302219  
 8 -3.487105 -1.724432  
 9 2.668759 1.594842  
10 -3.156485 3.191137  
11 3.165506 -3.999838  
12 -2.786837 -3.099354  
13 4.208187 2.984927  
14 -2.123337 2.943366  
15 0.704199 -0.479481  
16 -0.392370 -3.963704  
17 2.831667 1.574018  
18 -0.790153 3.343144  
19 2.943496 -3.357075  
20 -3.195883 -2.283926  
21 2.336445 2.875106  
22 -1.786345 2.554248  
23 2.190101 -1.906020  
24 -3.403367 -2.778288  
25 1.778124 3.880832  
26 -1.688346 2.230267  
27 2.592976 -2.054368  
28 -4.007257 -3.207066  
29 2.257734 3.387564  
30 -2.679011 0.785119  
31 0.939512 -4.023563  
32 -3.674424 -2.261084  
33 2.046259 2.735279  
34 -3.189470 1.780269  
35 4.372646 -0.822248  
36 -2.579316 -3.497576  
37 1.889034 5.190400  
38 -0.798747 2.185588  
39 2.836520 -2.658556  
40 -3.837877 -3.253815  
41 2.096701 3.886007  
42 -2.709034 2.923887  
43 3.367037 -3.184789  
44 -2.121479 -4.232586  
45 2.329546 3.179764  
46 -3.284816 3.273099  
47 3.091414 -3.815232  
48 -3.762093 -2.432191  
49 3.542056 2.778832  
50 -1.736822 4.241041  
51 2.127073 -2.983680  
52 -4.323818 -3.938116  
53 3.792121 5.135768  
54 -4.786473 3.358547  
55 2.624081 -3.260715  
56 -4.009299 -2.978115  
57 2.493525 1.963710  
58 -2.513661 2.642162  
59 1.864375 -3.176309  
60 -3.171184 -3.572452  
61 2.894220 2.489128  
62 -2.562539 2.884438  
63 3.491078 -3.947487  
64 -2.565729 -2.012114  
65 3.332948 3.983102  
66 -1.616805 3.573188  
67 2.280615 -2.559444  
68 -2.651229 -3.103198  
69 2.321395 3.154987  
70 -1.685703 2.939697  
71 3.031012 -3.620252  
72 -4.599622 -2.185829  
73 4.196223 1.126677  
74 -2.133863 3.093686  
75 4.668892 -2.562705  
76 -2.793241 -2.149706  
77 2.884105 3.043438  
78 -2.967647 2.848696  
79 4.479332 -1.764772  
80 -4.905566 -2.911070
View Code
  1 import numpy as np
  2 import matplotlib.pyplot as plt
  3 # 载入数据
  4 data = np.genfromtxt("kmeans.txt", delimiter=" ")
  5 
  6 plt.scatter(data[:,0],data[:,1])
  7 plt.show()
  8 print(data.shape)
  9 #训练模型
 10 # 计算距离
 11 def euclDistance(vector1, vector2):
 12     return np.sqrt(sum((vector2 - vector1) ** 2))
 13 
 14 
 15 # 初始化质心
 16 def initCentroids(data, k):
 17     numSamples, dim = data.shape
 18     # k个质心，列数跟样本的列数一样
 19     centroids = np.zeros((k, dim))
 20     # 随机选出k个质心
 21     for i in range(k):
 22         # 随机选取一个样本的索引
 23         index = int(np.random.uniform(0, numSamples))#从一个均匀分布[low,high)中随机采样
 24         # 作为初始化的质心
 25         centroids[i, :] = data[index, :]
 26     return centroids
 27 
 28 
 29 # 传入数据集和k的值
 30 def kmeans(data, k):
 31     # 计算样本个数
 32     numSamples = data.shape[0]
 33     # 样本的属性，第一列保存该样本属于哪个簇，第二列保存该样本跟它所属簇的误差
 34     clusterData = np.array(np.zeros((numSamples, 2)))
 35     # 决定质心是否要改变的变量
 36     clusterChanged = True
 37 
 38     # 初始化质心
 39     centroids = initCentroids(data, k)
 40 
 41     while clusterChanged:
 42         clusterChanged = False
 43         # 循环每一个样本
 44         for i in range(numSamples):
 45             # 最小距离
 46             minDist = 100000.0
 47             # 定义样本所属的簇
 48             minIndex = 0
 49             # 循环计算每一个质心与该样本的距离
 50             for j in range(k):
 51                 # 循环每一个质心和样本，计算距离
 52                 distance = euclDistance(centroids[j, :], data[i, :])
 53                 # 如果计算的距离小于最小距离，则更新最小距离
 54                 if distance < minDist:
 55                     minDist = distance
 56                     # 更新最小距离
 57                     clusterData[i, 1] = minDist
 58                     # 更新样本所属的簇
 59                     minIndex = j
 60 
 61                     # 如果样本的所属的簇发生了变化
 62             if clusterData[i, 0] != minIndex:
 63                 # 质心要重新计算
 64                 clusterChanged = True
 65                 # 更新样本的簇
 66                 clusterData[i, 0] = minIndex
 67 
 68         # 更新质心
 69         for j in range(k):
 70             # 获取第j个簇所有的样本所在的索引
 71             cluster_index = np.nonzero(clusterData[:, 0] == j)
 72             # 第j个簇所有的样本点
 73             pointsInCluster = data[cluster_index]
 74             # 计算质心
 75             centroids[j, :] = np.mean(pointsInCluster, axis=0)
 76         #         showCluster(data, k, centroids, clusterData)
 77 
 78     return centroids, clusterData
 79 
 80 
 81 # 显示结果
 82 def showCluster(data, k, centroids, clusterData):
 83     numSamples, dim = data.shape
 84     if dim != 2:
 85         print("dimension of your data is not 2!")
 86         return 1
 87 
 88         # 用不同颜色形状来表示各个类别
 89     mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', '<r', 'pr']
 90     if k > len(mark):
 91         print("Your k is too large!")
 92         return 1
 93 
 94         # 画样本点
 95     for i in range(numSamples):
 96         markIndex = int(clusterData[i, 0])
 97         plt.plot(data[i, 0], data[i, 1], mark[markIndex])
 98 
 99         # 用不同颜色形状来表示各个类别
100     mark = ['*r', '*b', '*g', '*k', '^b', '+b', 'sb', 'db', '<b', 'pb']
101     # 画质心点
102     for i in range(k):
103         plt.plot(centroids[i, 0], centroids[i, 1], mark[i], markersize=20)
104 
105     plt.show()
106 # 设置k值
107 k = 4
108 # centroids 簇的中心点
109 # cluster Data样本的属性，第一列保存该样本属于哪个簇，第二列保存该样本跟它所属簇的误差
110 centroids, clusterData = kmeans(data, k)
111 if np.isnan(centroids).any():
112     print('Error')
113 else:
114     print('cluster complete!')
115     # 显示结果
116 showCluster(data, k, centroids, clusterData)
117 print(centroids)
118 # 做预测
119 x_test = [0,1]
120 np.tile(x_test,(k,1))
121 # 误差
122 np.tile(x_test,(k,1))-centroids
123 # 误差平方
124 (np.tile(x_test,(k,1))-centroids)**2
125 # 误差平方和
126 ((np.tile(x_test,(k,1))-centroids)**2).sum(axis=1)
127 # 最小值所在的索引号
128 np.argmin(((np.tile(x_test,(k,1))-centroids)**2).sum(axis=1))
129 def predict(datas):
130     return np.array([np.argmin(((np.tile(data,(k,1))-centroids)**2).sum(axis=1)) for data in datas])
131 #画出簇的作用区域
132 # 获取数据值所在的范围
133 x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
134 y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
135 
136 # 生成网格矩阵
137 xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
138                      np.arange(y_min, y_max, 0.02))
139 
140 z = predict(np.c_[xx.ravel(), yy.ravel()])# ravel与flatten类似，多维数据转一维。flatten不会改变原始数据，ravel会改变原始数据
141 z = z.reshape(xx.shape)
142 # 等高线图
143 cs = plt.contourf(xx, yy, z)
144 # 显示结果
145 showCluster(data, k, centroids, clusterData)

下面这个demo是使用sklearn库实现聚类

 1 from sklearn.cluster import  KMeans
 2 import numpy as np
 3 from matplotlib import pyplot as plt
 4 data = np.genfromtxt('kmeans.txt',delimiter=" ")# 载入数据
 5 k = 4# 设置k值
 6 model = KMeans(n_clusters=4)# 训练模型
 7 model.fit(data)
 8 print(model.labels_)# 结果
 9 centers = model.cluster_centers_# 分类中心点坐标
10 print(centers)
11 result = model.labels_
12 mark = ['or','ob','og','oy']# 画出各个数据点，用不同颜色表示分类
13 for i,d in enumerate(data):
14     plt.plot(d[0],d[1],mark[result[i]])
15 mark  = ['*r','*b','*g','*y']# 画出各个分类的中心点
16 for i,center in enumerate(centers):
17     plt.plot(center[0],center[1],mark[i],markersize = 20)
18 plt.show()
19 x_min, x_max = data[:,0].min() - 1,data[:,0].max() +1# 获取数据值所在的范围
20 y_min, y_max = data[:,1].min() - 1,data[:,1].max() +1
21 xx ,yy= np.meshgrid(np.arange(x_min,x_max,0.02),np.arange(y_min,y_max,0.02))# 生成网格矩阵
22 z = model.predict(np.c_[xx.ravel(),yy.ravel()])
23 z = z.reshape(xx.shape)
24 cs = plt.contourf(xx,yy,z)# 等高线图
25 mark = ['or','ob','og','oy']
26 for i,d in enumerate(centers):
27     plt.plot(d[0],d[1],mark[result[i]])
28 mark  = ['*r','*b','*g','*y']
29 for i,center in enumerate(centers):
30     plt.plot(center[0],center[1],mark[i],markersize = 20)
31 plt.show()

当数据量很大的时候，会出现原始聚类算法效率很低，计算速度很慢，因此可以使用mini batch k-means在数据量很大的时候提高速度

 

 

 

 

 

 

 

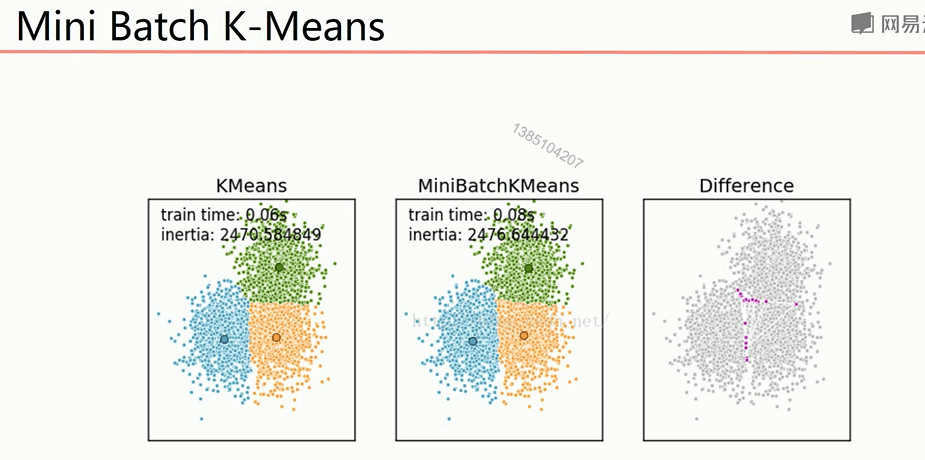
 1 from sklearn.cluster import  MiniBatchKMeans
 2 import numpy as np
 3 from matplotlib import pyplot as plt
 4 data = np.genfromtxt('kmeans.txt',delimiter=" ")# 载入数据
 5 k = 4# 设置k值
 6 model = MiniBatchKMeans(n_clusters=4)# 训练模型
 7 model.fit(data)
 8 print(model.labels_)# 结果
 9 centers = model.cluster_centers_# 分类中心点坐标
10 print(centers)
11 result = model.labels_
12 mark = ['or','ob','og','oy']# 画出各个数据点，用不同颜色表示分类
13 for i,d in enumerate(data):
14     plt.plot(d[0],d[1],mark[result[i]])
15 mark  = ['*r','*b','*g','*y']# 画出各个分类的中心点
16 for i,center in enumerate(centers):
17     plt.plot(center[0],center[1],mark[i],markersize = 20)
18 plt.show()
19 x_min, x_max = data[:,0].min() - 1,data[:,0].max() +1# 获取数据值所在的范围
20 y_min, y_max = data[:,1].min() - 1,data[:,1].max() +1
21 xx ,yy= np.meshgrid(np.arange(x_min,x_max,0.02),np.arange(y_min,y_max,0.02))# 生成网格矩阵
22 z = model.predict(np.c_[xx.ravel(),yy.ravel()])
23 z = z.reshape(xx.shape)
24 cs = plt.contourf(xx,yy,z)# 等高线图
25 mark = ['or','ob','og','oy']
26 for i,d in enumerate(centers):
27     plt.plot(d[0],d[1],mark[result[i]])
28 mark  = ['*r','*b','*g','*y']
29 for i,center in enumerate(centers):
30     plt.plot(center[0],center[1],mark[i],markersize = 20)
31 plt.show()

当然传统聚类算法有一些弊端（sklearn提供的Kmeans已经解决了下面两个问题），如下

 

 

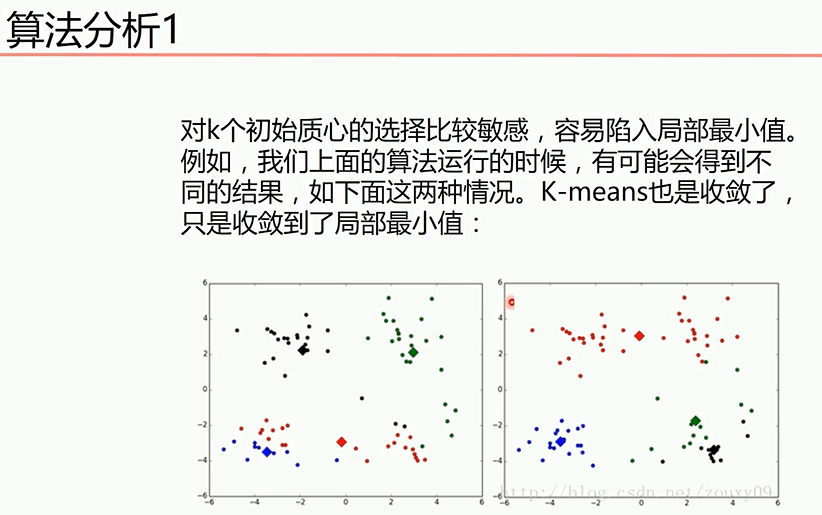
 该问题可以通过多次初始化随机点的选取，然后选择代价函数最小的那个

下面的demo实现了优化

  1 import numpy as np
  2 import matplotlib.pyplot as plt
  3 # 载入数据
  4 data = np.genfromtxt("kmeans.txt", delimiter=" ")
  5 
  6 
  7 # 计算距离
  8 def euclDistance(vector1, vector2):
  9     return np.sqrt(sum((vector2 - vector1) ** 2))
 10 
 11 
 12 # 初始化质心
 13 def initCentroids(data, k):
 14     numSamples, dim = data.shape
 15     # k个质心，列数跟样本的列数一样
 16     centroids = np.zeros((k, dim))
 17     # 随机选出k个质心
 18     for i in range(k):
 19         # 随机选取一个样本的索引
 20         index = int(np.random.uniform(0, numSamples))
 21         # 作为初始化的质心
 22         centroids[i, :] = data[index, :]
 23     return centroids
 24 
 25 
 26 # 传入数据集和k的值
 27 def kmeans(data, k):
 28     # 计算样本个数
 29     numSamples = data.shape[0]
 30     # 样本的属性，第一列保存该样本属于哪个簇，第二列保存该样本跟它所属簇的误差
 31     clusterData = np.array(np.zeros((numSamples, 2)))
 32     # 决定质心是否要改变的变量
 33     clusterChanged = True
 34 
 35     # 初始化质心
 36     centroids = initCentroids(data, k)
 37 
 38     while clusterChanged:
 39         clusterChanged = False
 40         # 循环每一个样本
 41         for i in range(numSamples):
 42             # 最小距离
 43             minDist = 100000.0
 44             # 定义样本所属的簇
 45             minIndex = 0
 46             # 循环计算每一个质心与该样本的距离
 47             for j in range(k):
 48                 # 循环每一个质心和样本，计算距离
 49                 distance = euclDistance(centroids[j, :], data[i, :])
 50                 # 如果计算的距离小于最小距离，则更新最小距离
 51                 if distance < minDist:
 52                     minDist = distance
 53                     # 更新样本所属的簇
 54                     minIndex = j
 55                     # 更新最小距离
 56                     clusterData[i, 1] = distance
 57 
 58             # 如果样本的所属的簇发生了变化
 59             if clusterData[i, 0] != minIndex:
 60                 # 质心要重新计算
 61                 clusterChanged = True
 62                 # 更新样本的簇
 63                 clusterData[i, 0] = minIndex
 64 
 65         # 更新质心
 66         for j in range(k):
 67             # 获取第j个簇所有的样本所在的索引
 68             cluster_index = np.nonzero(clusterData[:, 0] == j)
 69             # 第j个簇所有的样本点
 70             pointsInCluster = data[cluster_index]
 71             # 计算质心
 72             centroids[j, :] = np.mean(pointsInCluster, axis=0)
 73         #         showCluster(data, k, centroids, clusterData)
 74 
 75     return centroids, clusterData
 76 
 77 
 78 # 显示结果
 79 def showCluster(data, k, centroids, clusterData):
 80     numSamples, dim = data.shape
 81     if dim != 2:
 82         print("dimension of your data is not 2!")
 83         return 1
 84 
 85         # 用不同颜色形状来表示各个类别
 86     mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', '<r', 'pr']
 87     if k > len(mark):
 88         print("Your k is too large!")
 89         return 1
 90 
 91         # 画样本点
 92     for i in range(numSamples):
 93         markIndex = int(clusterData[i, 0])
 94         plt.plot(data[i, 0], data[i, 1], mark[markIndex])
 95 
 96         # 用不同颜色形状来表示各个类别
 97     mark = ['*r', '*b', '*g', '*k', '^b', '+b', 'sb', 'db', '<b', 'pb']
 98     # 画质心点
 99     for i in range(k):
100         plt.plot(centroids[i, 0], centroids[i, 1], mark[i], markersize=20)
101 
102     plt.show()
103 
104 
105 # 设置k值
106 k = 4
107 
108 min_loss = 10000
109 min_loss_centroids = np.array([])
110 min_loss_clusterData = np.array([])
111 
112 for i in range(50):
113     # centroids 簇的中心点
114     # cluster Data样本的属性，第一列保存该样本属于哪个簇，第二列保存该样本跟它所属簇的误差
115     centroids, clusterData = kmeans(data, k)
116     loss = sum(clusterData[:, 1]) / data.shape[0]
117     if loss < min_loss:
118         min_loss = loss
119         min_loss_centroids = centroids
120         min_loss_clusterData = clusterData
121 
122 #     print('loss',min_loss)
123 print('cluster complete!')
124 centroids = min_loss_centroids
125 clusterData = min_loss_clusterData
126 
127 # 显示结果
128 showCluster(data, k, centroids, clusterData)
129 # 做预测
130 x_test = [0,1]
131 np.tile(x_test,(k,1))
132 # 误差
133 np.tile(x_test,(k,1))-centroids
134 # 误差平方
135 (np.tile(x_test,(k,1))-centroids)**2
136 # 误差平方和
137 ((np.tile(x_test,(k,1))-centroids)**2).sum(axis=1)
138 # 最小值所在的索引号
139 np.argmin(((np.tile(x_test,(k,1))-centroids)**2).sum(axis=1))
140 def predict(datas):
141     return np.array([np.argmin(((np.tile(data,(k,1))-centroids)**2).sum(axis=1)) for data in datas])
142 # 获取数据值所在的范围
143 x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
144 y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
145 
146 # 生成网格矩阵
147 xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
148                      np.arange(y_min, y_max, 0.02))
149 
150 z = predict(np.c_[xx.ravel(), yy.ravel()])# ravel与flatten类似，多维数据转一维。flatten不会改变原始数据，ravel会改变原始数据
151 z = z.reshape(xx.shape)
152 # 等高线图
153 cs = plt.contourf(xx, yy, z)
154 # 显示结果
155 showCluster(data, k, centroids, clusterData)
View Code

关于k值选择，一个方法是肘部法，另一个方法是按照自己的需要选择分为几类，下面的demo是根据肘部法选择K值

  1 import numpy as np
  2 import matplotlib.pyplot as plt
  3 # 载入数据
  4 data = np.genfromtxt("kmeans.txt", delimiter=" ")
  5 
  6 
  7 # 计算距离
  8 def euclDistance(vector1, vector2):
  9     return np.sqrt(sum((vector2 - vector1) ** 2))
 10 
 11 
 12 # 初始化质心
 13 def initCentroids(data, k):
 14     numSamples, dim = data.shape
 15     # k个质心，列数跟样本的列数一样
 16     centroids = np.zeros((k, dim))
 17     # 随机选出k个质心
 18     for i in range(k):
 19         # 随机选取一个样本的索引
 20         index = int(np.random.uniform(0, numSamples))
 21         # 作为初始化的质心
 22         centroids[i, :] = data[index, :]
 23     return centroids
 24 
 25 
 26 # 传入数据集和k的值
 27 def kmeans(data, k):
 28     # 计算样本个数
 29     numSamples = data.shape[0]
 30     # 样本的属性，第一列保存该样本属于哪个簇，第二列保存该样本跟它所属簇的误差
 31     clusterData = np.array(np.zeros((numSamples, 2)))
 32     # 决定质心是否要改变的变量
 33     clusterChanged = True
 34 
 35     # 初始化质心
 36     centroids = initCentroids(data, k)
 37 
 38     while clusterChanged:
 39         clusterChanged = False
 40         # 循环每一个样本
 41         for i in range(numSamples):
 42             # 最小距离
 43             minDist = 100000.0
 44             # 定义样本所属的簇
 45             minIndex = 0
 46             # 循环计算每一个质心与该样本的距离
 47             for j in range(k):
 48                 # 循环每一个质心和样本，计算距离
 49                 distance = euclDistance(centroids[j, :], data[i, :])
 50                 # 如果计算的距离小于最小距离，则更新最小距离
 51                 if distance < minDist:
 52                     minDist = distance
 53                     # 更新样本所属的簇
 54                     minIndex = j
 55                     # 更新最小距离
 56                     clusterData[i, 1] = distance
 57 
 58             # 如果样本的所属的簇发生了变化
 59             if clusterData[i, 0] != minIndex:
 60                 # 质心要重新计算
 61                 clusterChanged = True
 62                 # 更新样本的簇
 63                 clusterData[i, 0] = minIndex
 64 
 65         # 更新质心
 66         for j in range(k):
 67             # 获取第j个簇所有的样本所在的索引
 68             cluster_index = np.nonzero(clusterData[:, 0] == j)
 69             # 第j个簇所有的样本点
 70             pointsInCluster = data[cluster_index]
 71             # 计算质心
 72             centroids[j, :] = np.mean(pointsInCluster, axis=0)
 73         #         showCluster(data, k, centroids, clusterData)
 74 
 75     return centroids, clusterData
 76 
 77 
 78 # 显示结果
 79 def showCluster(data, k, centroids, clusterData):
 80     numSamples, dim = data.shape
 81     if dim != 2:
 82         print("dimension of your data is not 2!")
 83         return 1
 84 
 85         # 用不同颜色形状来表示各个类别
 86     mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', '<r', 'pr']
 87     if k > len(mark):
 88         print("Your k is too large!")
 89         return 1
 90 
 91         # 画样本点
 92     for i in range(numSamples):
 93         markIndex = int(clusterData[i, 0])
 94         plt.plot(data[i, 0], data[i, 1], mark[markIndex])
 95 
 96         # 用不同颜色形状来表示各个类别
 97     mark = ['*r', '*b', '*g', '*k', '^b', '+b', 'sb', 'db', '<b', 'pb']
 98     # 画质心点
 99     for i in range(k):
100         plt.plot(centroids[i, 0], centroids[i, 1], mark[i], markersize=20)
101 
102     plt.show()
103 
104 
105 list_lost = []
106 for k in range(2, 10):
107     min_loss = 10000
108     min_loss_centroids = np.array([])
109     min_loss_clusterData = np.array([])
110     for i in range(50):
111         # centroids 簇的中心点
112         # cluster Data样本的属性，第一列保存该样本属于哪个簇，第二列保存该样本跟它所属簇的误差
113         centroids, clusterData = kmeans(data, k)
114         loss = sum(clusterData[:, 1]) / data.shape[0]
115         if loss < min_loss:
116             min_loss = loss
117             min_loss_centroids = centroids
118             min_loss_clusterData = clusterData
119     list_lost.append(min_loss)
120 
121 #     print('loss',min_loss)
122 # print('cluster complete!')
123 # centroids = min_loss_centroids
124 # clusterData = min_loss_clusterData
125 
126 # 显示结果
127 # showCluster(data, k, centroids, clusterData)
128 print(list_lost)
129 plt.plot(range(2,10),list_lost)
130 plt.xlabel('k')
131 plt.ylabel('loss')
132 plt.show()
133 # 做预测
134 x_test = [0,1]
135 np.tile(x_test,(k,1))
136 # 误差
137 np.tile(x_test,(k,1))-centroids
138 # 误差平方
139 (np.tile(x_test,(k,1))-centroids)**2
140 # 误差平方和
141 ((np.tile(x_test,(k,1))-centroids)**2).sum(axis=1)
142 # 最小值所在的索引号
143 np.argmin(((np.tile(x_test,(k,1))-centroids)**2).sum(axis=1))
144 def predict(datas):
145     return np.array([np.argmin(((np.tile(data,(k,1))-centroids)**2).sum(axis=1)) for data in datas])
146 # 获取数据值所在的范围
147 x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
148 y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
149 
150 # 生成网格矩阵
151 xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
152                      np.arange(y_min, y_max, 0.02))
153 
154 z = predict(np.c_[xx.ravel(), yy.ravel()])# ravel与flatten类似，多维数据转一维。flatten不会改变原始数据，ravel会改变原始数据
155 z = z.reshape(xx.shape)
156 # 等高线图
157 cs = plt.contourf(xx, yy, z)
158 # 显示结果
159 showCluster(data, k, centroids, clusterData)
View Code

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

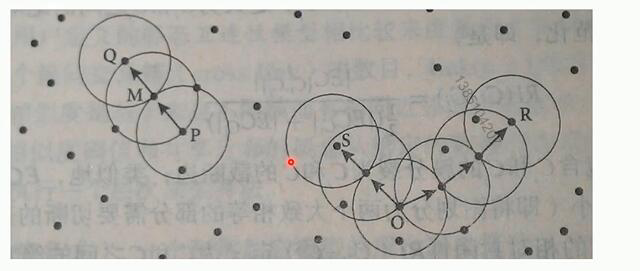
from sklearn.cluster import DBSCAN
import numpy as np
from matplotlib  import  pyplot as plt
data = np.genfromtxt("kmeans.txt",delimiter=' ')
model = DBSCAN(eps=1.5,min_samples=4)
model.fit(data)
result = model.fit_predict(data)
print(result)
mark = ['or', 'ob', 'og', 'oy', 'ok', 'om']
for i,d in enumerate(data):
    plt.plot(d[0],d[1],mark[result[i]])
plt.show()
 1 import numpy as np
 2 import matplotlib.pyplot as plt
 3 from sklearn import datasets
 4 x1, y1 = datasets.make_circles(n_samples=2000, factor=0.5, noise=0.05)
 5 x2, y2 = datasets.make_blobs(n_samples=1000, centers=[[1.2,1.2]], cluster_std=[[.1]])
 6 
 7 x = np.concatenate((x1, x2))
 8 plt.scatter(x[:, 0], x[:, 1], marker='o')
 9 plt.show()
10 from sklearn.cluster import KMeans
11 y_pred = KMeans(n_clusters=3).fit_predict(x)
12 plt.scatter(x[:, 0], x[:, 1], c=y_pred)
13 plt.show()
14 from sklearn.cluster import DBSCAN
15 y_pred = DBSCAN().fit_predict(x)
16 plt.scatter(x[:, 0], x[:, 1], c=y_pred)
17 plt.show()
18 y_pred = DBSCAN(eps = 0.2).fit_predict(x)
19 plt.scatter(x[:, 0], x[:, 1], c=y_pred)
20 plt.show()
21 y_pred = DBSCAN(eps = 0.2, min_samples=50).fit_predict(x)
22 plt.scatter(x[:, 0], x[:, 1], c=y_pred)
23 plt.show()

 

 

posted @ 2019-11-12 21:16  你的雷哥  阅读(1069)  评论(0)  编辑  收藏  举报