覃秉丰机器学习_概述

因此覃秉丰的机器学习视频还是比较不错的，所以学习一下，写个几篇博客做个个人笔记，就这样而已。

 

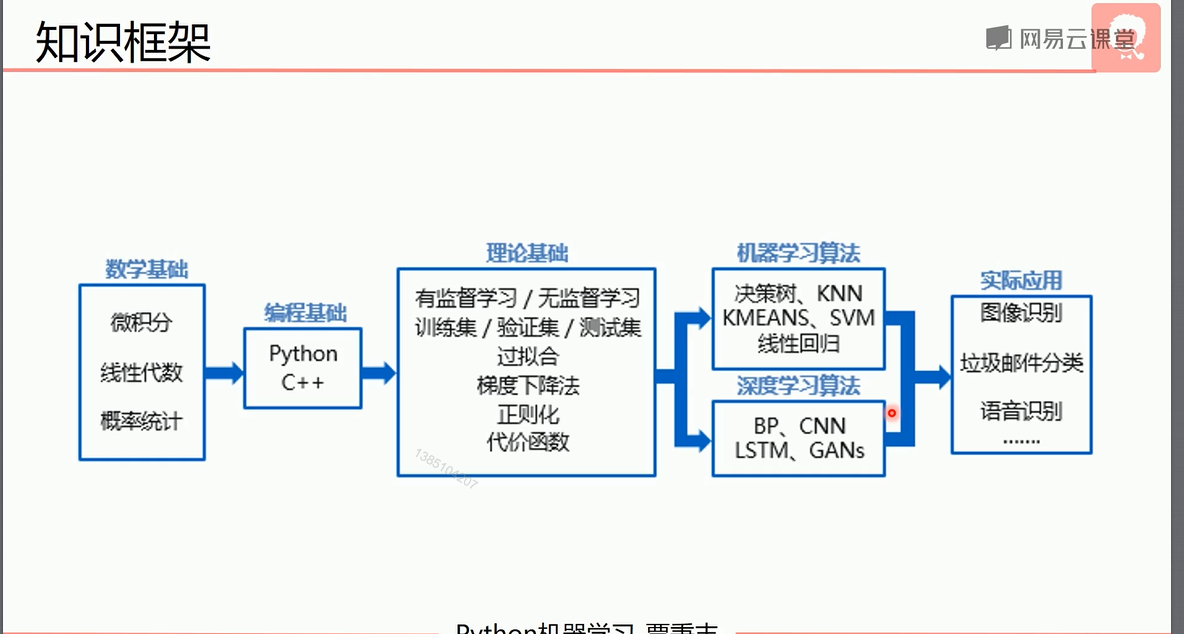
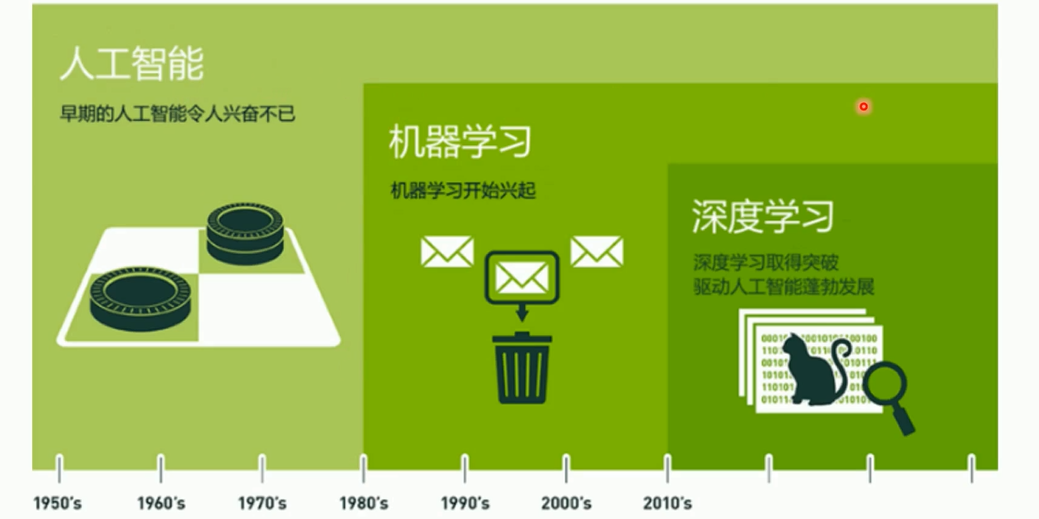
 Q:人工智能和机器学习深度学习之前的关系。

对于数据集比较小的情况机器学习效果要好于深度学习

 

 Q:训练集，验证集，测试集

 

 

 Q:有监督学习，无监督学习，半监督学习

监督学习(supervised learning)是指用已经标记好的数据(labelled data)，做训练来预测新数据的类型(class)，或者是值。预测已有类型叫做分类(classification)，预测一个值叫做回归(regression)。

无监督学习(unsupervised learning)是指不需要提前对数据做标记，直接对它们做聚类(clustering)。

更多的内容看我的另一篇文章：有监督学习和无监督学习

那么什么是半监督学习(semi-supervised learning)呢？其实就和它的名字一样，同时用了有监督学习的方法和无监督的方法，更准确的说是同时用了标记好的数据(labelled data)和未标记的数据(unlabelled data) 。总结上面所说的监督学习用于分类和回归，无监督学习用于聚类，那么半监督学习的目的是什么呢？目的是用现有的数据训练出更好的数据模型。要知道，现在占主导地位的还是有监督学习，如何更好的利用无监督学习还是一个正在研究的话题，之所以需要开发他的原因是我们不需要人工的给数据打标签，这样会非常省事。从这里可以得知，虽然我们现在可以有海量的数据，但是其中只有很少一部分是有标签的。所以半监督学习就是要同时利用有标记的数据和没标记的数据。 举个例子：

 

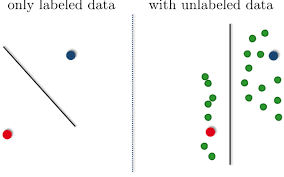
假设上图中红点和蓝点表示两类数据class1,class2。绿点表示没有被标记的数据。如果现在我们用支持向量机(SVM)，仅对有标记的数据分类，那么分割线如左图所示。但是其实真是情况是，如果我们不忽略未做标记的数据，数据的分布其实是如右图所示的。那么一个更好的划分线也应该是如右图所示的垂直线。这就是半监督学习的基本原理。

 Q:聚类，分类，拟合（回归）

 

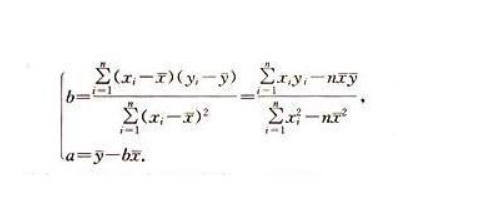
对于一次函数的拟合使用的是最小二乘法，下面是Python的一个实现demo

import numpy as np
from matplotlib import pyplot as plt

def fitSLR(X,Y):#使用最小二乘法求一次方程的系数k,b
    x_avg = np.sum(X) / len(X)
    y_avg = np.sum(Y) / len(Y)
    fen_zi, fen_mu = 0, 0
    for i in range(len(X)):
        fen_zi += (X[i] - x_avg) * (Y[i] - y_avg)
        fen_mu += (X[i] - x_avg) ** 2
    k = fen_zi/fen_mu
    b = y_avg - k * x_avg
    return k, b
def predict(x, k, b):#由k,b,x求y
    return k * x + b

X = [1.5, 0.8, 2.6, 1.0, 0.6, 2.8, 1.2, 0.9, 0.4, 1.3, 1.2, 2.0, 1.6, 1.8, 2.2]
Y = [3.1, 1.9, 4.2, 2.3, 1.6, 4.9, 2.8, 2.1, 1.4, 2.4, 2.4, 3.8, 3.0, 3.4, 4.0]

k, b = fitSLR(X, Y);
print('k = ', k)
print('b = ', b)

plt.figure()
plt.scatter(X, Y)
y_max = predict(max(X), k, b)
y_min = predict(min(X), k, b)
plt.plot([min(X), max(X)], [y_min, y_max], 'r-')#关于plot的用法可以参考https://blog.csdn.net/feng98ren/article/details/79392747
plt.show()

下面的demo是关于画图的一个小例子

import numpy as np
from matplotlib import pyplot as plt
X = [1, 2, 3, 4, 6]
Y = [3.1, 1.9, 4.2, 2.3, 1.6]
X = np.array(X)
Y = np.array(Y)
X1 = X * 2
plt.figure()
plt.rcParams['font.sans-serif'] = 'SimHei'#设置中文显示，否则可能无法显示中文或者是各种字符错乱
plt.rcParams['axes.unicode_minus'] = False
plt.xlabel('x轴标签')
plt.ylabel('y轴标签')
plt.title('线形图demo')
plt.xticks(np.arange(1, 6),['s1','s2','s3','s4','s5'],rotation = 45)#第一个参数是坐标轴各个点位置，第二个参数是x轴下标显示lable参数，rotation代表lable显示的旋转角度
plt.plot(X1, Y, 'r--')
plt.plot(X, Y, 'b')
plt.legend(['线条一', '线条二'])
plt.savefig('D:/demo.png')#注意要先保存再show
plt.show()

下面的链接是关于multiply()、dot()、 matmul()、' * '、'@'对于数组和矩阵在运算上体现的是叉乘和点乘的区别的总结

Python numpy 矩阵乘法multiply()、dot()、 matmul()、' * '、'@'辨析

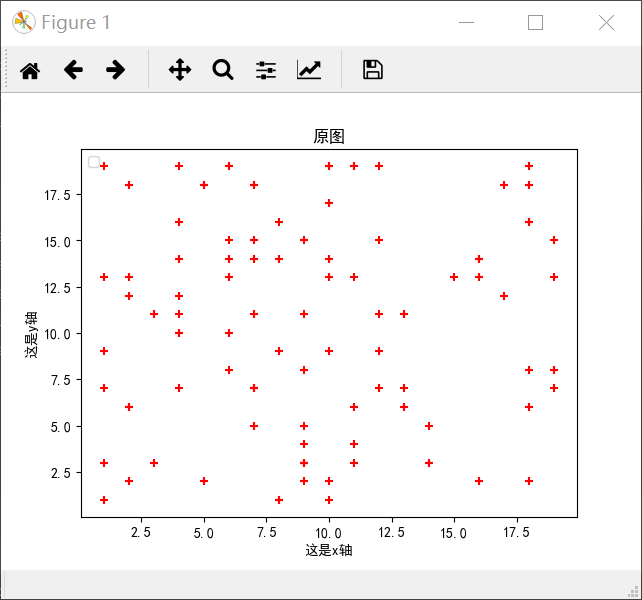
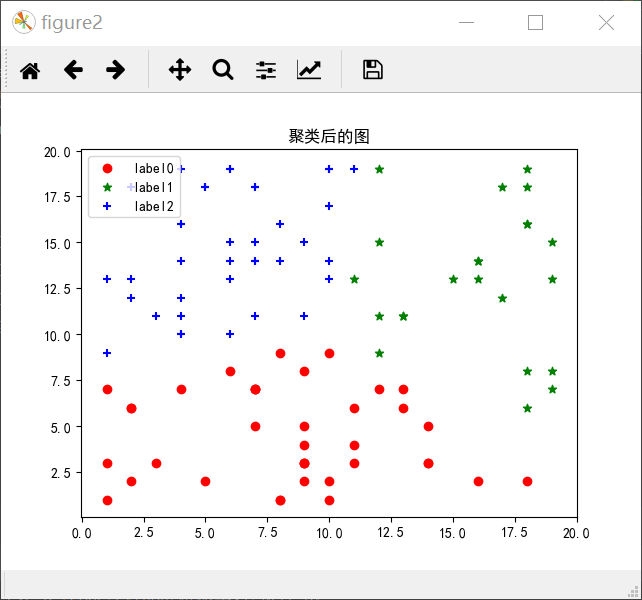
下面是一个关于聚类的demo

   

import numpy as np
from matplotlib import pyplot as plt
from sklearn.cluster import KMeans

X = np.random.randint(1, 20, [100,2])#产生一个100*2的随机矩阵
print(X.shape)
plt.figure()#默认是figure1
plt.rcParams['font.sans-serif'] = 'SimHei'#保证汉字正常显示出来
plt.rcParams['axes.unicode_minus'] = False
plt.title('原图')
plt.scatter(X[:, 0], X[:, 1], marker='+', color = 'r')#显示原图
plt.xlabel('这是x轴')
plt.ylabel('这是y轴')
plt.legend(loc = 2)
plt.show()

plt.figure('figure2')
plt.title('聚类后的图')
estimator = KMeans(n_clusters= 3)#生成聚成三类的聚类器
estimator.fit(X)#聚类
label_pred = estimator.labels_# 获取聚类标签
x0 = X[label_pred == 0]
x1 = X[label_pred == 1]
x2 = X[label_pred == 2]
plt.scatter(x0[:,0], x0[:, 1],c = 'red', marker= 'o', label = 'label0')
plt.scatter(x1[:,0], x1[:, 1],c = 'green', marker= '*', label = 'label1')
plt.scatter(x2[:,0], x2[:, 1],c = 'blue', marker= '+', label = 'label2')
plt.legend(loc = 2)
plt.show()

 

 

 关于Python随机数的使用可以参看这篇博客

我们可以使用pytorch框架对数据进行分类处理，可以参考之这篇博客：

莫烦PyTorch学习笔记(五)——分类