概率论概念总结
随机变量
何谓随机变量？即给定样本空间
，其上的实值函数
称为(实值)随机变量。
期望
离散随机变量的一切可能值与其对应的概率P的乘积之和称为数学期望
方差
一个随机变量的方差（Variance）描述的是它的离散程度，也就是该变量离其期望值的距离
协方差
在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。
相关系数
衡量随机变量X与Y相关程度的一种方法，相关系数的取值范围是[-1,1]。相关系数的绝对值越大，则表明X与Y相关度越高。当X与Y线性 时， 相关系数取值为1（正线性相关）或-1（负线性相关）。
中心极限定理
心极限定理说明，在适当的条件下，大量相互独立随机变量的均值经适当标准化后依分布收敛于正态分布。这组定理是数理统计学和误差分析的理 论基础，指出了大量随机变量之和近似服从正态分布的条件。并且呈正态分布。
贝叶斯公式
P(h∣D)=P(h)P(D∣h)/P(D)
贝叶斯定理是关于随机事件A和B的条件概率的一则定理。其中P是在B发生的情况下A发生的可能性，把x关于y的后验概率，转换成了y关于x的后验概率和先验概率，简单说，把不好计算的条件概率转换为好计算的条件概率
全概率公式
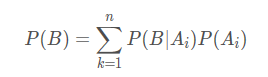设实验E的样本空间为S,A为E的事件,B1,B2,...,Bn为S的一个划分,且P(Bi)>0(i=1,2,...,n),则
P(A)=P(A|B1)*P(B1) + P(A|B2)*P(B2) + ... + P(A|Bn)*P(Bn).
上式称为全概率公式
全概率公式的作用在于将复杂事件的概率求解转化为在不同情况下发生的简单事件的概率求和
样本空间
定义：随机试验E的所有结果构成的集合称为E的 样本空间，记为S={e}，称S中的元素e为样本点，一个元素的单点集称为基本事件．
大数定理
在试验不变的条件下，重复试验多次，随机事件的频率近似于它的概率。偶然中包含着某种必然。
常用抽样分布
假设检验
在整个总体分布未知或仅知道形式，但各种参数未知，仅有一些测试的样本数据的场景下，提出某种假设。利用样本，验证假设的合理性。
先验概率
事情未发生，只根据以往数据统计，分析事情发生的可能性，即先验概率。
后验概率
事情已发生，已有结果，但求引起这事发生的因素的可能性，有果求因，即后验概率。 后验概率，引起的原因，是测量可能错误。
后验概率的计算，是以先验概率为前提条件的。如果只知道事情结果，而不知道先验概率（没有以往数据统计），是无法计算后验概率的。
后验概率的计算需要应用到贝叶斯公式
置信区间
求满足某个概率的区间。 即可以理解为，在这个范围内，达到某种可信度，可信概率。
主成分分析
是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。广泛应用到降维里面去
条件概率，联合概率，边缘概率
条件概率就是事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P（A|B），读作“在B条件下A的概率”
联合概率表示两个事件共同发生的概率。A与B的联合概率表示为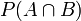
或者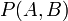
。
边缘概率是某个事件发生的概率。边缘概率是这样得到的：在联合概率中，把最终结果中不需要的那些事件合并成其事件的全概率而消失（对离 散随机变量用求和得全概率，对连续随机变 量用积分得全概率）。这称为边缘化（marginalization）。A的边缘概率表示为P（A），B的边缘 概率表示为P（B）。
最大似然估计
在已知实验结果的情况下，用来估计满足这些样本分布的参数，把可能性最大的那个参数θθ作为真实θ^θ^的参数估计。说的通俗一点：最大似然估计就是利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。
2> 对似然表达式求导，必要时进行预处理，比如取对数（逻辑回归需要），令其导数为0，得到似然方程。
3> 求解似然方程，得到的参数解即为极大似然估计的解。
离散型随机变量
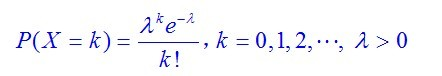
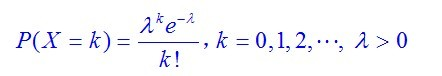
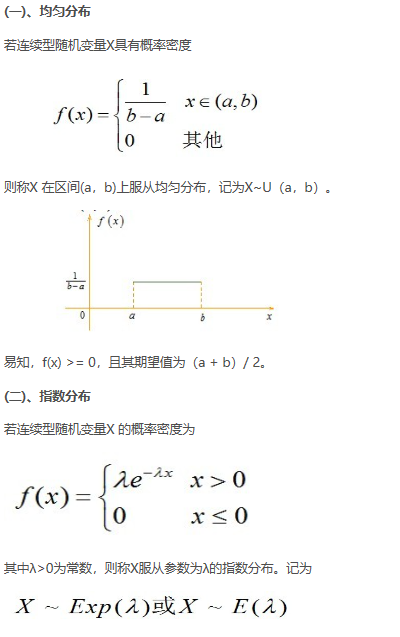
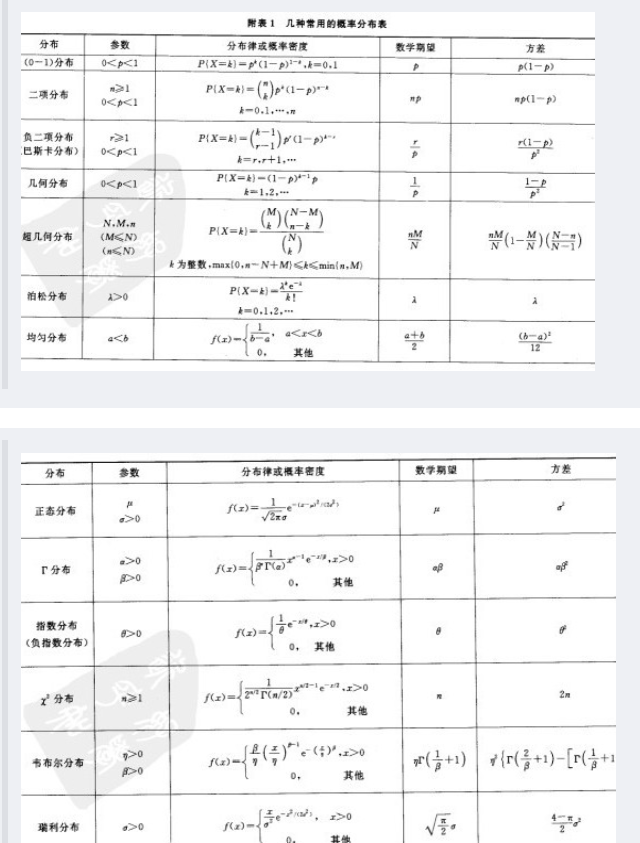
连续型随机变量
