根据前序、中序、后序遍历还原二叉树

参考：https://blog.csdn.net/changjiale110/article/details/79489884

！首先我们得知道概念：

前序遍历：先访问当前节点，再访问当前节点的左子树，最后访问当前节点的右子树。对于二叉树，深度遍历与此同。规律：根在前；子树在根后且左子树比右子树靠前，且第一个就是根节点；

中序遍历：先访问当前节点的左子树，然后访问当前节点，最后是当前节点的右子树，二叉树，中序遍历会得到数据升序效果。规律：根在中；左子树在跟左边，右子树在根右边，左边部分是根结点的左子树的中序遍历序列，右边部分是根结点的右子树的中序遍历序列 ；

后序遍历：先访问当前节点的左子树，然后是当前节点的又子树，最后是当前节点。规律：根在后；子树在根前且左子树比右子树靠前，且最后一个节点是根节点。

一、前序+中序

1根据前序序列的第一个元素建立根结点；
2在中序序列中找到该元素，确定根结点的左右子树的中序序列；
3在前序序列中确定左右子树的前序序列；
4由左子树的前序序列和中序序列建立左子树；
5由右子树的前序序列和中序序列建立右子树。
如：已知一棵二叉树的先序遍历序列和中序遍历序列分别是abdgcefh、dgbaechf，求二叉树及后序遍历序列。
先序：abdgcefh—>a bdg cefh
中序：dgbaechf—->dgb a echf

得出结论：a是树根，a有左子树和右子树，左子树有bdg结点，右子树有cefh结点。
先序：bdg—>b dg

中序：dgb —>dg b

得出结论：b是左子树的根结点，b无右子树，有左子树。
先序：dg—->d g

中序：dg—–>dg

得出结论：d是b左子树的根节点,d无左子树，g是d的右子树

然后对于a 的右子树类似可以推出

最后还原： a

 

后序遍历：gdbehfca

二、后序+中序：

已知一棵二叉树的后序序列和中序序列，构造该二叉树的过程如下：
1. 根据后序序列的最后一个元素建立根结点；
2. 在中序序列中找到该元素，确定根结点的左右子树的中序序列；
3. 在后序序列中确定左右子树的后序序列；
4. 由左子树的后序序列和中序序列建立左子树；
5. 由右子树的后序序列和中序序列建立右子树

如还是上面题目：如：已知一棵二叉树的后序遍历序列和中序遍历序列分别是gdbehfca、dgbaechf，求二叉树

后序：gdbehfca—->gdb ehfc a

中序：dgbaechf—–>dgb a echf
得出结论：a是树根，a有左子树和右子树，左子树有bdg结点，右子树有cefh结点。
后序：gdb—->gd b

中序：dgb—–>dg b

得出结论：b是a左子树的根节点，无右子树，有左子树dg。

后序：gd—->g d

中序：dg—–>d g

得出结论：d是b的左子树根节点，g是d的右子树。

然后对于a 的右子树类似可以推出。然后还原。
三、前序+后序

前序和后序在本质上都是将父节点与子结点进行分离，但并没有指明左子树和右子树的能力，因此得到这两个序列只能明确父子关系，而不能确定一个二叉树。 故此法无。不能唯一确定一个二叉树。

 代码如下（为了方便结点用数字表示）

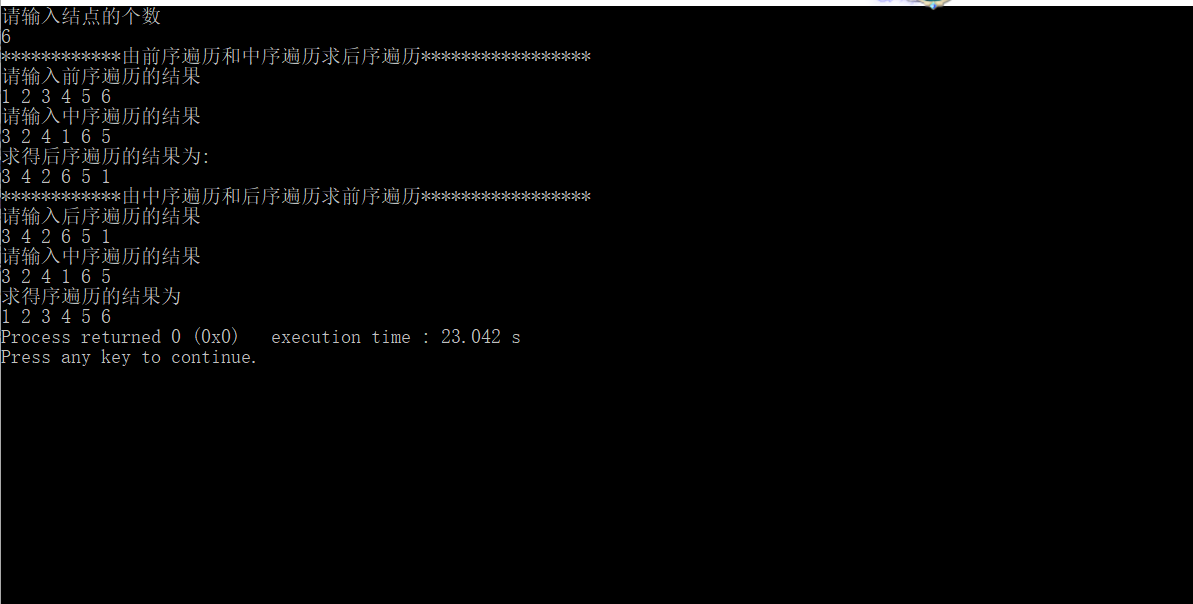
#include<bits/stdc++.h>
using namespace std;
int n;
int pre[100];
int in[100];
int back[100];
void get(int root,int start,int end)//求后序遍历结果
{
    if(start>end  )
        return ;
    int i=start;
    while(i<end  && in[i]!=pre[root]) i++;
    get(root+1,start,i-1);
    get(root+1+i-start,i+1,end);
    cout << pre[root] << " ";

}
void get1(int root,int start,int end)//求前序遍历结果
{
      if(end<start)
        return ;
      int i=end;
      while(i>start && in[i]!=back[root]) i--;
       cout << back[root] << " ";
      get1(root-1+i-end,start,i-1);
      get1(root-1,i+1,end);

}
int main()
{

    cout << "请输入结点的个数" << endl;
    cin >> n;

    cout << "************由前序遍历和中序遍历求后序遍历*****************" <<endl;;
    cout << "请输入前序遍历的结果" << endl;

    memset(pre,0,sizeof(pre));
    for(int i=0;i<n;i++)
    {
        cin >> pre[i];
    }
     cout << "请输入中序遍历的结果" << endl;

    memset(in,0,sizeof(in));
    for(int i=0;i<n;i++)
    {
        cin >> in[i];
    }
    cout << "求得后序遍历的结果为:" <<endl;
   get(0,0,n-1);
   cout << endl;

    cout << "************由中序遍历和后序遍历求前序遍历*****************" <<endl;
    memset(back,0,sizeof(back));
    memset(pre,0,sizeof(pre));
    cout << "请输入后序遍历的结果" << endl;
    for(int i=0;i<n;i++)
    {
        cin >> back[i];
    }
    cout << "请输入中序遍历的结果" << endl;
    for(int i=0;i<n;i++)
    {
        cin >> in[i];
    }
    cout << "求得前序遍历的结果为" << endl;
    get1(n-1,0,n-1);
    return 0;
}