归并排序

归并排序 (merge sort) 是一类与插入排序、交换排序、选择排序不同的另一种排序方法。归并的含义是将两个或两个以上的有序表合并成一个新的有序表。归并排序有多路归并排序、两路归并排序 , 可用于内排序，也可以用于外排序。这里仅对内排序的两路归并方法进行讨论。

一、两路归并排序算法思路

分而治之(divide - conquer);每个递归过程涉及三个步骤
第一, 分解: 把待排序的 n 个元素的序列分解成两个子序列, 每个子序列包括 n/2 个元素.
第二, 治理: 对每个子序列分别调用归并排序MergeSort, 进行递归操作
第三, 合并: 合并两个排好序的子序列,生成排序结果.

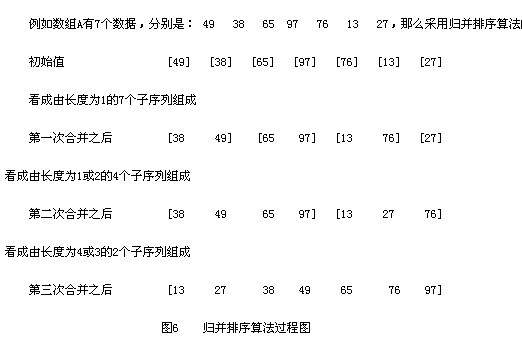
二、算法实现
　　此算法的实现不像图示那样简单，现分三步来讨论。首先从宏观上分析，首先让子表表长 L=1 进行处理；不断地使 L=2*L ，进行子表处理，直到 L>=n 为止，把这一过程写成一个主体框架函数 mergesort 。然后对于某确定的子表表长 L ，将 n 个记录分成若干组子表，两两归并，这里显然要循环若干次，把这一步写成一个函数 mergepass ，可由 mergesort 调用。最后再看每一组（一对）子表的归并，其原理是相同的，只是子表表长不同，换句话说，是子表的首记录号与尾记录号不同，把这个归并操作作为核心算法写成函数 merge ，由 mergepass 来调用。假设我们有一个没有排好序的序列，那么首先我们使用分割的办法将这个序列分割成一个一个已经排好序的子序列，然后再利用归并的方法将一个个的子序列合并成排序好的序列。分割和归并的过程可以看下面的图例。

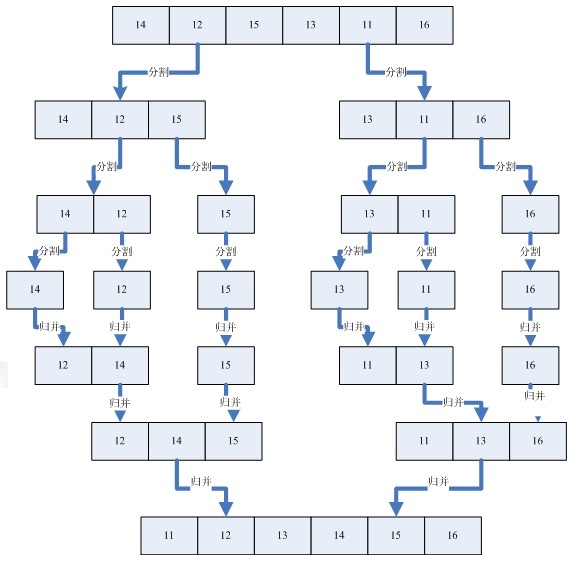
三、代码实现

package Sort;

import java.util.Scanner;

public class MergeSort {

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        Scanner scan=new Scanner(System.in);
        int n=scan.nextInt();
        int[] arr=new int[n];
        for(int i=0;i<n;i++) {
            arr[i]=scan.nextInt();
        }
        sort(arr,0,arr.length-1);
        for(int i=0;i<arr.length;i++) {
            System.out.print(arr[i]+" ");
        }
    }
    public static void sort(int[] arr,int left,int right) {
        if(left>=right) {
            return;
        }
        else {
            int mid=(left+right)/2;
            sort(arr,left,mid);
            sort(arr,mid+1,right);
            merge(arr,left,mid,right);
        }
    }
    public static void merge(int[] arr,int left,int mid,int right) {
        //创建临时数组
        int[] temp=new int[right-left+1];
        int i=left;
        int j=mid+1;
        int k=0;
        //把较小的数移到新数组中
        while(i<=mid&&j<=right) {
            if(arr[i]<arr[j]) {
                temp[k++]=arr[i++];
            }
            else {
                temp[k++]=arr[j++];
            }
        }
        //一边移入完成后将另一边的全部移入
        //将左边剩下的全部移入
        while(i<=mid) {
            temp[k++]=arr[i++];
        }
        //将右边剩下的全部移入
        while(j<=right) {
            temp[k++]=arr[j++];
        }
        //把新数组中的数覆盖原数组
        for(int l=0;l<temp.length;l++) {
            arr[l+left]=temp[l];
        }
    }

}