树分块学习笔记
本文主要参考 周欣 《浅谈一类树分块的构建算法及其应用》
-
\(\operatorname{top cluster}\) 的概念
一个树簇(\(\operatorname{cluster}\)) 是一个树上的连通子图, 有至多两个点和全树外部相接。
这两个点称为界点, 其它的包含在里面的点叫内点。 两个界点之间的路径称为簇路径(\(\operatorname{cluster path}\))。
簇是可以合并的, 具体来说有 \(\operatorname{compress}\) 和 \(\operatorname{rake}\) 两种操作,
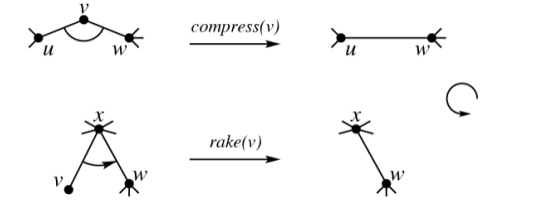
可以证明经过上面两个操作后整个树会变成一个簇, 合并的过程会形成一棵二叉树, 称为 \(\operatorname{top tree}\), 与本文关系不大, 故略去。
-
树分块的基本结构
基本思想 : 把一棵树经过划分划分成若干个簇的并, 把所有的界点与它们的簇路径建成一棵新的树,这棵树称为收缩树。

设每个簇大小为 \(B\), 则会划分出 \(\dfrac n B\) 个簇。
可以发现,这与分块的结构很类似, 界点和簇路径可以看成整块, 中间夹着的内点看成散块,于是只要我们能够快速维护出这些信息,就可以很方便的解决许多问题。
-
树分块的构建
算法 : DFS 寻找哪些点需要成为界点,再根据界点找到簇路径即可,用一个栈维护当前未归类的边。
只有在下面 3 种情况发生时,把当前点设为界点 :
- 当前点为根,我们强制规定根必须是界点.
- 当前点有两个或以上含有界点的子树 .
- 栈中的边数大于等于 \(B\) .
容易证明这三种情况的总发生次数不会超过 \(2 \times \dfrac n B\) 次。
问题抽象为给定一个数 \(m\) 及两个序列 \(a\)(表示各个子树中未归类的数量),\(b\)(各个子树中是否存在界点)
我们要做的是,将序列切割成若干子段,使得每一段中 \(a\) 的和不大于 \(B\),且 \(b\) 的和最多为 \(1\)。
可以直接贪心,每次截取最长的合法前缀,证明略。 这样的块的总数是不超过 \(6 \times \dfrac n B\)的。

