手撸机器学习算法 - 逻辑回归

系列文章目录：

算法介绍

今天我们一起来学习使用非常广泛的分类算法：逻辑回归，是的，你没有看错，虽然它名字里有回归，但是它确实是个分类算法，作为除了感知机以外，最最最简单的分类算法，下面我们把它与感知机对比来进行学习；

从决策边界上看

感知机：决策边界就是类别的分界线，处于错误一侧的点即为分类错误点；
逻辑回归：决策边界表示分为正类和负类均为50%，数据点被分为正类的概率直观上由其到决策边界的距离决定；

以上，对于数据中的噪声，假设噪声点实际为负类，但是被分到正类一侧，如果是感知机，则无法判断，而逻辑回归以概率为基础，如果该噪声点实际被分为正类的概率仅为52%，那么实际上它属于负类的可能性也很大，即逻辑回归认为数据的产生是有一定随机性的，相比于简单的0或1，概率值更能表现其实际情况；

输出函数

从决策边界可知，感知机的输出∈{+1,-1}，而逻辑回归的输出为0~1的概率值：

感知机使用sign作为输出函数：sign(wx+b)
逻辑回归使用sigmoid作为概率输出函数：sigmoid(wx+b)，sigmoid=1/(1+e^-z)，这里z=wx+b，可以看到当z=0时，也就是处于决策边界时，此时sigmoid= 0.5，也就是50%，除此之外，z越大，sigmoid输出越大，可以认为越有可能是正类，反之即为负类，且可以通过极限推导sigmoid区间为(0,1)；

如何看待逻辑回归选择Sigmoid作为概率输出函数呢，可以从以下几个点来理解：

sigmoid自身性质：
1. 输入是整个实数域，输出是(0,1)，输出不包含0和1，使得对于机器学习仅使用整体的一部分作为样本进行训练的场景，很适合处理未出现在样本集中的类别；
2. 图像曲线对于两侧极值不敏感，二分类的输出符合伯努利分布，输入一般认为符合正态分布，图像曲线也符合这一点；
3. 易于求导，sigmoid函数的导数为S(wx+b)*(1-S(wx+b))，参数优化过程基本就是求导过程，因此易于求导很重要；
贝叶斯概率推导：
1. sigmoid函数可以由伯努利、正态分布+贝叶斯全概率公式推导得到；

损失函数

感知机：\(yi*sign(w*xi+b)\)，yi∈{-1,+1}，模型分类正确返回值为+1，错误返回值为-1，对所有样本进行求和即可得到score值；
逻辑回归：\(ln(1+e^{-(yi*wxi)})\)，yi∈{-1,+1}，模型分类正确返回值>=0，错误返回值<0，负数绝对值越大，表示错误越严重，对所有样本计算该误差加起来求平均即为逻辑回归的误差函数；

算法推导

从概率角度看Sigmoid

Sigmoid给出了条件概率：

正类的分布：\(P(Y=1|X) = Sigmoid(wx+b) = \frac{1}{1+e^{-(wx+b)}}\)，其中x~P(X)，y~P(Y)；
负类的分布：\(P(Y=-1|X) = 1-Sigmoid(wx+b) = 1-\frac{1}{1+e^{-(wx+b)}}\)；

函数优化求导

首先列出损失函数如下：

\[\frac{1}{N}\sum_{i=1}^N\ln(1+e^{-y_iwx_i}), yi\in{\{+1,-1\}} \]

对上述函数针对参数w求梯度：

\[\begin{equation*} \begin{split} \frac{\partial \frac{1}{N}\sum_{i=1}^{N}ln(1+e^{-y_iwx_i})}{\partial w} = \frac{1}{N}\sum_{i=1}^{N}[\frac{(-y_ix_i)(e^{-y_iwx_i})}{1+e^{-y_iwx_i}}] \end{split} \end{equation*} \]

上述梯度就是后续我们用于更新参数w的依据；

代码实现

初始化相关参数

def __init__(self,X,y,epochs=5000,eta=0.1,epsilon=0.001):
    super(LogisticRegression,self).__init__(X,y)
    self.epochs = epochs
    self.eta = eta
    self.epsilon = epsilon
    self.wk = np.array([0 for i in range(self.X.shape[1])])

Sigmoid

def sigmoid(self,x):
    return 1/(1+np.exp(-x))

经验损失函数梯度

def drhd(self,w):
    '''
    经验误差函数的梯度
    '''
    ew = []
    for i in range(self.X.shape[1]):
        ewi = np.mean(-self.y*self.X[:, i]*np.exp(-self.y*(self.X@w))/(1+np.exp(-self.y*(self.X@w))))
        ew.append(ewi)
    return np.array(ew)

迭代训练

def train(self):
    i_,norm = None,None
    for i in range(self.epochs):
        drhdwk = self.drhd(self.wk)
        i_,norm = i,np.linalg.norm(drhdwk)
        if np.linalg.norm(drhdwk) < self.epsilon:
            break
        self.wk = self.wk-self.eta*drhdwk
    return i_,norm,self.wk

运行结果

先看下感知机-口袋算法处理非线性分类问题：

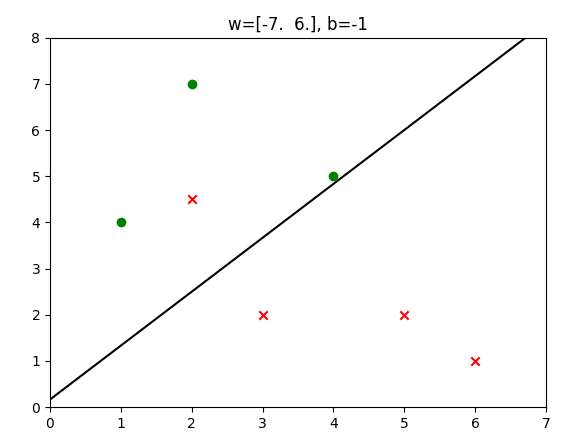
再来对比看下逻辑回归的分类情况：

直觉上看，二者虽然都有一个点分类错误（这是肯定的，因为数据不是线性可分的），但是对于分类错误的×来说，逻辑回归中错误的×距离分割平面更近，也就是说模型对于这个点的判断是比较模糊而不是很肯定的，可以认为是错的不严重，这一点也会反应在损失函数中；

全部代码

import numpy as np
from 线性回归最小二乘法矩阵实现 import LinearRegression as LR
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

class LogisticRegression(LR):
    def __init__(self,X,y,epochs=5000,eta=0.1,epsilon=0.001):
        super(LogisticRegression,self).__init__(X,y)
        self.epochs = epochs
        self.eta = eta
        self.epsilon = epsilon
        self.wk = np.array([0 for i in range(self.X.shape[1])])

    def sigmoid(self,x):
        return 1/(1+np.exp(-x))

    def h(self,x):
        '''
        假设函数
        '''
        return self.sigmoid(x@self.wk.T)

    def drhd(self,w):
        '''
        经验误差函数的梯度
        '''
        ew = []
        for i in range(self.X.shape[1]):
            ewi = np.mean(-self.y*self.X[:, i]*np.exp(-self.y*(self.X@w))/(1+np.exp(-self.y*(self.X@w))))
            ew.append(ewi)
        return np.array(ew)

    def train(self):
        i_,norm = None,None
        for i in range(self.epochs):
            drhdwk = self.drhd(self.wk)
            i_,norm = i,np.linalg.norm(drhdwk)
            if np.linalg.norm(drhdwk) < self.epsilon:
                break
            self.wk = self.wk-self.eta*drhdwk
        return i_,norm,self.wk

    def sign(self,value):
        return 1 if value>=0 else -1

    def predict(self,x):
        return self.sign(self.wk.dot(np.append([1],x)))

if __name__ == '__main__':
    X = np.array([[5,2], [3,2], [2,7], [1,4], [6,1], [4,5], [2,4.5]])
    y = np.array([-1, -1, 1, 1, -1, 1, -1, ])
    # X = np.array([[5,2], [3,2], [2,7], [1,4], [6,1], [4,5]])
    # y = np.array([-1, -1, 1, 1, -1, 1, ])
    iris = load_iris()
    X = iris.data[iris.target<2,:2]
    y = iris.target[iris.target<2]
    y[y==0] = -1

    model = LogisticRegression(X=X,y=y,epochs=10000,eta=.2,epsilon=0.0001)
    i,norm,w = model.train()
    print(f"epochs={i} -> w={w} -> norm={norm:>.8f}")
    for xi,yi in zip(X,y):
        print(yi,model.predict(xi))

    w,b = w[1:],w[0]
    positive = [x for x,y in zip(X,y) if y==1]
    negative = [x for x,y in zip(X,y) if y==-1]
    line = [(-w[0]*x-b)/w[1] for x in [-100,100]]
    plt.title('w='+str(w)+', b='+str(b))
    plt.scatter([x[0] for x in positive],[x[1] for x in positive],c='green',marker='o')
    plt.scatter([x[0] for x in negative],[x[1] for x in negative],c='red',marker='x')
    plt.plot([-100,100],line,c='black')
    plt.xlim(min([x[0] for x in X])-1,max([x[0] for x in X])+1)
    plt.ylim(min([x[1] for x in X])-1,max([x[1] for x in X])+1)
    plt.show()

    iris = load_iris()
    X = iris.data
    y = iris.target
    model = LogisticRegression(X=X,y=y,epochs=1000000,eta=.1,epsilon=0.0005)
    i,norm,w = model.train()
    print(f"epochs={i} -> w={w} -> norm={norm:>.8f}")

最后

逻辑回归几乎是机器学习中应用最为广泛的一种分类算法，由于其简单的思想、良好的数学理论、超强的可解释性，使得在推荐领域、金融领域等发挥了巨大的作用；

posted @ 2021-06-24 16:05 HoLoong 阅读(562) 评论(1) 编辑收藏举报

刷新页面返回顶部

Ho Loong

机器学习、深度学习、数据挖掘、游戏、心理学、WOW