算法总结：递归优化，二路归并，快速幂

文章目录

• 递归优化
• • 原版递归
  • 递归优化
• 二路归并
• • 正向二路归并
  • 逆向二路归并
• 快速幂
• • 取模运算法则
  • 快速幂
  • 位优化

递归优化

举例说明：

斐波那契数列 ： 求1 1 2 3 5 …
爬楼梯： 每次走1步或者2步，第一层有一种走法，第二层有两种走法 …

问题归纳：

---

归纳为这类问题的通项公式： f(x)=f(x−1)+f(x−2)

---

原版递归

优点： 简单，容易理解。
缺点： 1、出现冗余程序分支 2、对于较大数据的计算会使用较多的堆栈内存 3、同样是处理较大数据时，可能会爆栈。

//普通递归
int fibonaqie(int num)
{
	if (num == 1 || num == 2)
	{
		return 1;
	}
	return fibonaqie(num - 1) + fibonaqie(num - 2);
}

但是这种方式会出现冗余数据： 我们只需要求一次 f(4 3 2 1) 就是我们想要的答案，但是，这样递归显然会遇到重复的数据，并且我们还不能跳过它，只能重新调用，这样就会有大量的冗余数据的出现。

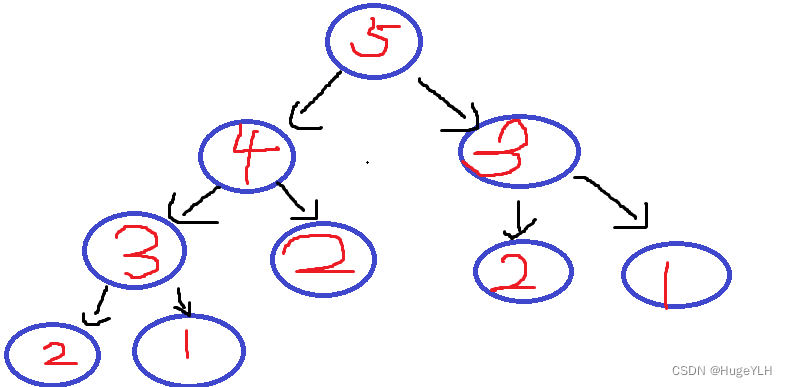
但是事实上，我们貌似只需要一个数组保存每次出现的值就可以，然后如果有重复数据则直接从数组返回，就可以解决这个问题。

---

递归优化

思路：
使用数组保存出现的每一个值，当我们进入函数时，首先检查我们所需要的这一项的值有没有之前出现过，如果之前出现过，则直接返回此数组的值就可以，没必要再次重复递归。

int fibonaqieplus(int num, int* arr)
{
	//出现了这一项：数组的值大于0，则说明这个数字之前被递归计算过，直接返回
	if (arr[num] > 0)
	{
		return arr[num];
	}

	//没有出现过某一项，则进行递归，给数组赋值
	if (num == 1 || num == 2)
	{
		arr[num] = 1;
	}
	else
	{
		arr[num] = fibonaqieplus(num - 1, arr) + fibonaqieplus(num - 2, arr);
	}
	//每次都赋予数组值，并且返回数组的值
	return arr[num];
}

//空间换时间
int FuncNum(int num)
{
	//数组首先初始化为0，为后面返回做准备
	int* arr = new int[num + 1]{};
	return fibonaqieplus(num, arr);
}

图解：计算 f(7)

• 红字是每次递归后计算的返回值。
• 绿字表示数组每次会存储某一项的值。
• 蓝字表示这一项以前出现过（这一项数组的值不为零），直接返回这个数值。
  

---

二路归并

引例：
leetcode 第88题：

合并两个有序数组：
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

示例：
输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]

正向二路归并

关于二路归并的详细的操作，请看我的另一篇博客：
链表与顺序表的二路归并操作 详细解析

关于两个数组的合并成为一个新的数组，我们很容易就想到二路归并的思想：

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        int index=0;
        int i=0,j=0;
        vector<int> dst(m+n);
        while (i<m || j<n)
        {
            if (i==m)
            {
                dst[index]=nums2[j];
                j++;
            }
            else if (j==n)
            {
                dst[index]=nums1[i];
                i++;
            }
            else if (nums1[i]>nums2[j])
            {
                dst[index]=nums2[j];
                j++;
            }
            else
            {
                dst[index]=nums1[i];
                i++;
            }
            index++;
        }

        copy(dst.begin(),dst.end(),nums1.begin());
    }
};

• 时间复杂度：O(m+n)。 指针移动单调递增，最多移动 m+n次，因此时间复杂度为 O(m+n)O(m+n)O(m+n)。

• 空间复杂度：O(m+n)。 需要建立长度为 m+n的中间数组。

通过二路归并，我们可以很轻松的解决这个问题，但是，我们实现的并不完美，我们创建了一个临时的数组来存储我们的元素，这样做未免空间开销有点大，有没有什么办法能够让我们能够利用很少的空间来实现这个问题呢？

---

逆向二路归并

有题目可以知道： 数组1后面为数组2保留了空间， 即：
[1,2,3,5,0,0,0,0] ， [1,2,3,4] …

所以我们可以利用从后往前的二路归并来解决，这样我们就不用临时开辟空间，从后往前进行二路归并。

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        int index=m+n-1;
        int i=m-1,j=n-1;
        int temp=0;
        while (i>=0 || j>=0)
        {
            if (i==-1)
            {
                temp=nums2[j--];
            }
            else if (j==-1)
            {
                temp=nums1[i--];
            }
            else if (nums1[i]>nums2[j])
            {
                temp=nums1[i--];
            }
            else
            {
                temp=nums2[j--];
            }
            nums1[index--]=temp;
        }
    }
};

说明：

• 我们对数组进行从后往前插入，因此最初的索引是 m+n-1。
• 对两个数组进行二路归并是从他们的尾部开始的，每操作一次，对应数组的索引减一，因此到最后某一个数组的索引会变成 -1 ，说明某一个数组结束，继续进行对另一个数组的插入。

时间复杂度：O(m+n)。 指针移动单调递减，最多移动 m+n 次，因此时间复杂度为 O(m+n)。

空间复杂度：O(1)。 直接对数组操作。

---

快速幂

引入：

a**b%c的值： a的b次幂，然后取余c

我们使用最简单的pow函数来计算：

llnum Power2(int a, int b)
{
	llnum res = 1;
	for (int i = 0; i < b; i++)
	{
		res = res * a;
	}
	return res % 1000;
}
printf("%lld\n", Power2(2, 100000000));

你会发现我们根本计算不出来，因为这个数字的大小，已经超过了long long的范围了，所以一定是错的，但是我就是想要把这个结果给算出来，你要怎么算呢？？？

取模运算法则

关于这三个公式的证明，在这里不说明了。

(a + b) % p = (a % p + b % p) % p （1）
(a - b) % p = (a % p - b % p ) % p （2）
(a * b) % p = (a % p * b % p) % p （3）

式子（三）表示，我们如果要计算两个数字的乘积，然后取余一个数字，取得它的结果。

这正好与我们的题目描述一致： a的b次幂，然后取余c，即取得这个数字的最后c位。
因此，我们计算的幂也是因此：

(a * a * a * a * a * a * a …（b个a）) % p
我们可以表示为： a是底数，b是指数
(a%p * a%p * a%p * a%p …（一共b个）) % p

即：

llnum fastPower1(int a, int b)
{
	llnum res = 1;
	for (int i = 0; i < b; i++)
	{
		res = res * a;
		res = res % 1000;
	}
	return res % 1000;	//最后再取余一个C
}
printf("%lld\n", fastPower1(2, 100000000));

我们就可以对每次的结果单独取余这个数字，然后最终的结果就是我们所得到的数字，答案是 376
但是我们又发现了一个严重的问题： 我们计算这一个数字耗时 12秒！！！！
时间！！！！！！！！ 时间开销过长，虽然这个数字不太符合实际，但是为了追求完美，我们不允许它花费这么长的时间。

---

快速幂

我们想想一下：

计算 3^10 你会怎么算？

一般人肯定会：分解这个式子。

1. 3 ^ 10 ：（3的10次方）
2. 9 ^ 5： （9的五次方）
3. 9 * 81 ^ 2： （9乘以81的二次方）
4. 9 * 6561 ^ 1：（9乘以6561的一次方）
5. 我们得出结果，计算机计算两个数字是非常快的。

我们通过分解，可以快速的解析一个幂的运算，虽然这个式子在标准库函数的pow计算也是忽略不计的，但是如果我们计算 3 ^ 1000000000 ，计算机通过自带的函数就无法实现了。

回归正题：
通过计算 3 ^ 10，底数为3，指数为10，因为指数是偶数，可以直接取底数的平方，然后指数除以二，得到 9 ^ 5；
指数是5是奇数，底数是9，将指数整除2， 然后底数平方，再外面在单独乘以一个底数，得到 9 * 81 ^ 2；
指数是2，偶数，底数是81，将指数整除2，底数平方 …

---

结论：

• 无论指数是奇数还是偶数，底数平方，指数整除二。
• 如果指数是奇数，还需要单独乘一个底数。
• 如果指数是偶数，则无需乘一个底数。

函数实现： a ^ b
快速幂完整代码：

typedef long long llnum;
llnum fast_power(int a, int b)
{
	llnum res = 1;
	while (b)
	{
		if (b % 2 == 1)
		{
			//如果指数是奇数，单独乘一个底数
			res = res * a;
		}
		//无论是指数奇偶，都要做的操作：
		b = b / 2;	//指数整除2
		a = a * a;	//底数平方
	}
	return res;
}

快速幂算法现在我们已经实现了，我们到最后再来用位运算进行一次优化，现在首先解决我们刚刚的问题： a ^ b % c 的时间开销过大的问题！！

---

接着我们再来实现 a ^ b % c：

typedef long long llnum;
llnum fast_power(int a, int b, int c)
{
	llnum res = 1;
	while (b)
	{
		if (b % 2 == 1)
		{
			//如果指数是奇数，单独乘一个底数
			res = res * a % c; //每次相乘后取余再相乘下一个
		}
		//无论是指数奇偶，都要做的操作：
		b = b / 2;	//指数整除2
		a = a * a % c;	//底数平方后取余C
	}
	return res;
}
printf("%lld\n", fast_power(2, 100000000,1000));

答案： 376 ，耗时0.02ms ，这比我们刚才的12秒优化太多了。。。

位优化

取余 2 的等不等于1 的判断：
int是四字节型数据： 按位与： 全 1 为 1；有0 则 0。
0x xxxxxxx1h 按位与 0x00000001 ：一定为 1
0x xxxxxxx0h 按位与 0x00000001 ：一定为 0

右移： >> 与除以2 同理； <<与乘以2 同理

typedef long long llnum;
llnum fast_power(int a, int b)
{
	llnum res = 1;
	while (b)
	{
		if (b & 0x1)	//b%2==1
		{
			res = res * a;
		}
		b >>= 1;		//b=b/2
		a = a * a;
	}
	return res;
}