四种质数筛选算法总结(c++)

文章目录

• 质数筛选
• • 枚举法
  • 埃氏筛
  • 线氏筛
  • 奇数筛

参考自： leetcode题解，计数质数

质数筛选

质数：除了1和它本身以外不再有其他因数的自然数。

合数：与质数相反。

枚举法

枚举法是查找质数最容易想到的方法，又被称为试除法。

它的思路就是遍历从2到n这个数的所有的数字，判断这个数字能否被这个序列种的任意一个序列整除，如果整除，则说明它不具有唯一的因子（1和它本身）

代码如下：

int func(int n)
{
    int ans = 0;
    bool isPrimer;
    for (int i = 2; i < n; i++)
    {
        isPrimer = true;		//默认其是一个质数
        for (int j = 2; j < i; j++)
        {
            if (i % j == 0)
            {	//如果有任意一个数能够被整除，则说明其一定不是质数，则直接退出
                isPrimer = false;
                break;
            }
        }
        if (isPrimer)	//如果是质数，则递增
        {
            ans++;
        }
    }
    return ans;
}

枚举优化

观察以下数字的形式：

4： 1 * 4 ，2 * 2 ， 4 * 1

5： 1* 5 ，sqrt(5) * sqrt(5) ， 5 * 1

6： 1* 6 ，2 * 3 ，sqrt(6) * sqrt(6) ，3 * 2 ， 6 * 1

8： 1* 6 ，2 * 4 ，sqrt(8) * sqrt(8) ，4 * 2 ， 6 * 1

可以得到，无论数字是质数还是合数，可以认为以中间的两个因子相乘，他们的左右两边是一致的。也就是说，遍历了前面，我们如果继续遍历，则会导致重复的现象出现，则我们完全可以避免他。

优化一个地方：

...
for (int j=2;j<=sqrt(i);j++)	//只遍历前面的sqrt部分即可
...

---

埃氏筛

引论： 一个质数的倍数一定是合数 ，如 3 是一个质数，则 3 * 3 ， 3 * 3 + 3 ， 3 * 3 + 3 + 3 一定是合数。

所以我们可以在准备判断一个数字是否是质数的时候，计算他的倍数，把他后面的倍数都计算出来，然后他们一定是合数，我们可以直接排除。

我们怎么实现这一点呢，可以定义一个质数数组，一共有n个数字，则用n个数字 1 填充数组。

1. 依次取出每一个数字，当其在数组里为1时，则它是一个质数。
2. 计算这个数字的倍数，则这些数字一定是合数，它所对应的数组里全部都置为0。
3. 质数数组里：为1：质数，为0：合数。

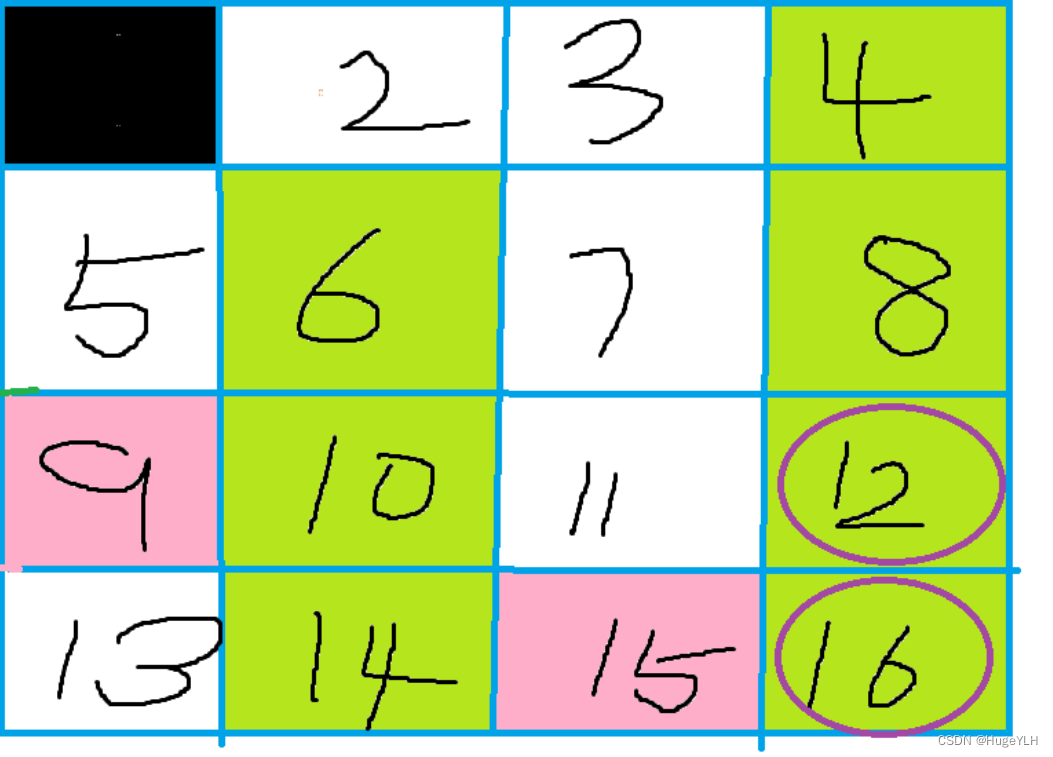
图解：

1. 绿色区域：数字2影响的区域（即是2的倍数），他们都是合数，直接在数组中标记为 0
2. 粉色区域： 数字3影响的区域， 同理 。。。。
3. 一个弊端：不同的数字会产生重合的情况，比如 2 和 3 他们的倍数都会选到 12这个数字，但是12在2的时候就被标记了，就没必要第二次重复标记了，因此这是一个埃氏筛需要优化的地方。。
   

//埃氏筛
int countPrimes_2(int n) {
    //首先全部初始化为1   
    vector<int> isPrimer(n, 1);
    int ans = 0;
    for (int i = 2; i < n; i++)
    {
        if (isPrimer[i] == 1)
        {
            ans++;
            if ((long long) i*i < n)	//注意首先判断第一个 i*i是否位于这个区间种
            {
                //将其 x(x+1) x(x+2) 倍数全部设置为0，即一定是非奇数
                for (int j = i * i; j < n; j += i)
                {
                    isPrimer[j] = 0;
                }
           	}
        }
    }
    return ans;
}

---

线氏筛

在埃氏筛中，我们存储重复标记元素的情况，我们无法避免它，但是我们利用线氏筛来完全避免这种情况。

根据《算术基本定理》：

算术基本定理： 任何一个大于1的 自然数 N,如果N不为 质数 ，那么N可以 唯一 分解成有限个质数的乘积.

例如：

• 16是一个合数，16可以 分解为 2 * 2 * 2 *2 是一个唯一的，有限个的质数乘积。

• 20 是一个合数，20 可以分解为 2 * 2 * 5 也是一个唯一的，有限个的质数的乘积。

因此得到结论：

• 有限多个质数的乘积 一定是一个合数 ---->质数 * 质数 * 质数 … = 合数

• 作为因子的每个质数不同，则最终的合数也不同。

• 临时存储每一个质数，只要后面的数字能够被这些质数整除，则直接结束循环，原因：

  • 当前数 能被 质数数组中的某质数 整除，当前数一定是包含 该质数 的合数

  • 合数拆分时，因子中，会出现 两个相同质数，不能保证合数不同

  • 质数数组中后面质数都比 该质数 大。该质数 * >它的质数 = 合数后面一定会遇到

图例：

1. 首先看数字2，它是质数，然后把这个数字放在质数数组[ 0 ]中，在确保范围的情况下，然后把2 依次乘以质数数组中每一项，得到的数字一定是合数（质数 * 质数 = 合数），由此，得到 4是合数，则标记为非质数 0。
2. 再来看数字3，它是质数，放入质数数组 [ 1 ]中，在确保范围的情况下，把3依次乘以质数数组中的每一项，得到6 和 9 因此，这两个数字也一定是合数，标识为 0。
3. 再来看数字4，它是合数，因此不用放入质数数组中，在确保范围的情况下，用4乘以质数数组中的每一项，得到 8 （ 4 * 2），你是否以为还是有数字12？ 答案是并没有，因为，数字4能被质数数组中的第一项（2）整除，我的理解： 12可以被拆分为 2 * 2 * 3，2和3都在质数数组中出现了，因此就没有必要再利用3 * 4得到 12了，因为4可以由 2 * 2得到，因此直接结束此次循环。
4. 数字5，确定 10 和 15 不是质数 …

//线氏筛
    int countPrimes_1(int n) {
        vector<int> primes;
        vector<int> isPrime(n, 1);
        for (int i = 2; i < n; ++i) {
            if (isPrime[i]) {
                primes.push_back(i);
            }
            for (int j = 0; j < primes.size() && i * primes[j] < n; ++j) {
                isPrime[i * primes[j]] = 0;
                if (i % primes[j] == 0) {
                    break;
                }
            }
        }
        return primes.size();
    }

---

奇数筛

优化后的埃氏筛：

• 偶数一定不是质数！ 因此只遍历每一个奇数就可以
• 奇数 * 偶数 = 偶数，因此不必讨论这种情况。
• 奇数 * 奇数 =奇数，因此只在奇数范围内寻找。

class Solution {
public:
    int countPrimes(int n) {
        //默认全部为true
        vector<int> primer(n,1);
        int res=(n>2)?1:0;
        int t=0;
        for (int i=3;i<n;i+=2)
        {
            if (primer[i]==1)
            {
                res++;
                if ((long long)i*i < n)
                {
                    for (int j=i;(t=i*j)<n;j+=2)
                    {
                        primer[t]=0;
                    }
                }
            }
        }
        return res;
    }
};