并查集
首先,并查集是用来区分群体,树的双亲作为并查集的存储结构,每一个集合用一棵树来表示,根节点的双亲指针为一个负数,表示元素的个数
初始化:
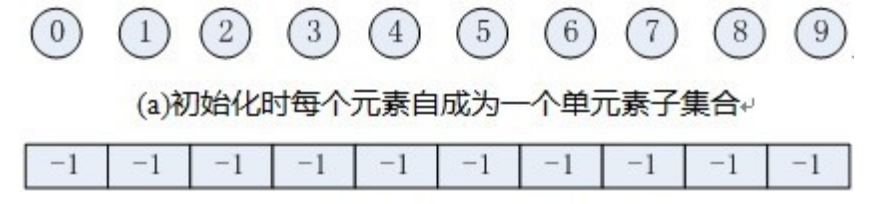
小变化
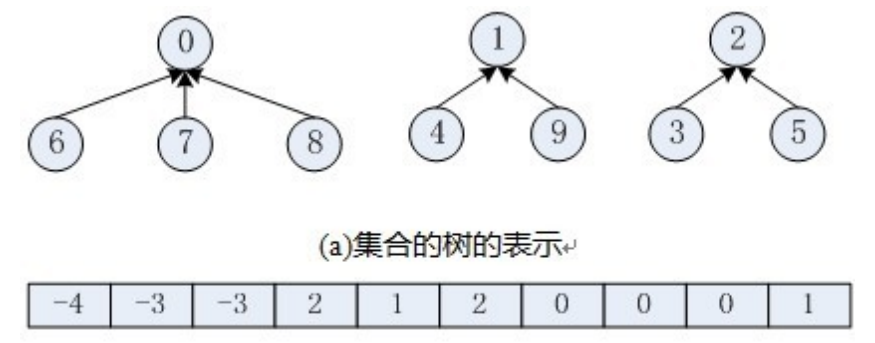
合并:
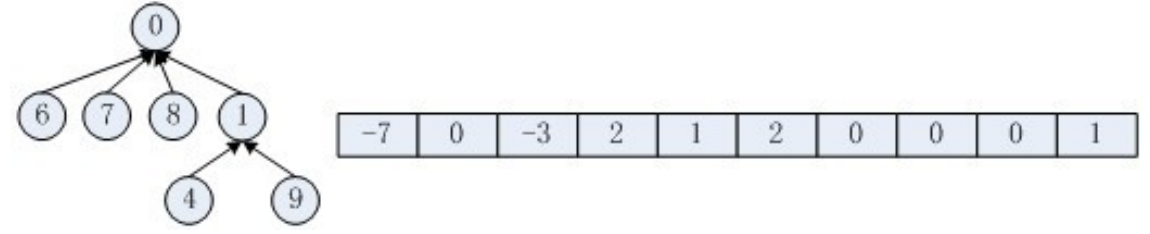
操作代码:

//自我实现 并查集 //a[]={1,2,3,4,5,6,7} #include<iostream> using namespace std; const int maxn=100; int parent[maxn]; int n,i,j; void ufset(){ for(i=1;i<=n;i++) parent[i]=-1; } int find(int x){ int s; for(s=x;parent[x]>=0;s=parent[s]); return s; } //将两个不同集合元素进行合并,使两个集合任意两元素可以连通 void Union(int R1,int R2){ int r1=find(R1),r2=find(R2); int tmp=parent[r1]+parent[r2];//负数 if(parent[r1]>parent[r2]) { parent[r1]=r2; parent[r2]=tmp; } else { parent[r2]=r1; parent[r1]=tmp; } } int find2(int x){ int s; for(s=x;parent[s]>=0;s=parent[s]); while(x!=s){ int tmp=parent[x]; parent[x]=s; x=tmp; //递推 } } int main() { }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号