内部收益率

题目描述
在金融中，我们有时会用内部收益率IRR来评价项目的投资财务效益，它等于使得投资净现值NPV等于0的贴现率。换句话说，给定项目的期数T、初始现金流CF0和项目各期的现金流CF1, CF2, ...，CFT，IRR是下面方程的解：

                                                

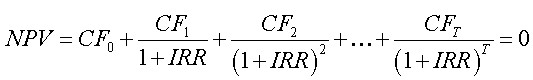
为了简单起见，本题假定：除了项目启动时有一笔投入（即初始现金流CF0 < 0）之外，其余各期均能赚钱（即对于所有i=1,2,...,T，CFi > 0）。根据定义，IRR可以是负数，但不能大于-1。

输入
 输入文件最多包含25组测试数据，每个数据占两行，第一行包含一个正整数T（1<=T<=10），表示项目的期数。第二行包含T+1个整数：CF0, CF1, CF2, ..., CFT，其中CF0 < 0, 0 < CFi < 10000 (i=1,2,...,T)。T=0表示输入结束，你的程序不应当处理这一行。

输出
 对于每组数据，输出仅一行，即项目的IRR，四舍五入保留小数点后两位。如果IRR不存在，输出"No"，如果有多个不同IRR满足条件，输出"Too many"（均不含引号）

样例输入
1
-1 2
2
-8 6 9
0
样例输出
1.00
0.50

分析：简单点就是求方程的解，四舍五入保留最后两位，所以要计算到最后三位，

1.枚举IRR的范围（-00，-1】V（0，++00）；

注意事项:该题中函数npv（IRR）在IRR∈（-1，+∞）上是递减的，故最多有一个根；

大佬很嚣张的解答：

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int main(void)
{
   int a[100],i,j,k,n,x;
   while(scanf("%d",&n) && n)
   {
       for(i=0;i<=n;i++)  scanf("%d",a+i);
       double x=-1.0+1e-5,y=1e6,irr,npv;
       for(j=0;j<100;j++)
       {
           irr=(x+y)/2;
           npv=0;
           for(k=0;k<=n;k++) npv+=1.0*a[k]/pow(1+irr,k);
           if(fabs(npv) < 1e-6)  break;
           if(npv < 0) y=irr;
           if(npv > 0) x=irr;
       }
       printf("%.2lf\n",irr);
   }
    return 0;
}