最小生成树
对计算机进行组网,需要在不同计算机之间建立连线,目标是使所有的计算机联通,且维护成本最低。
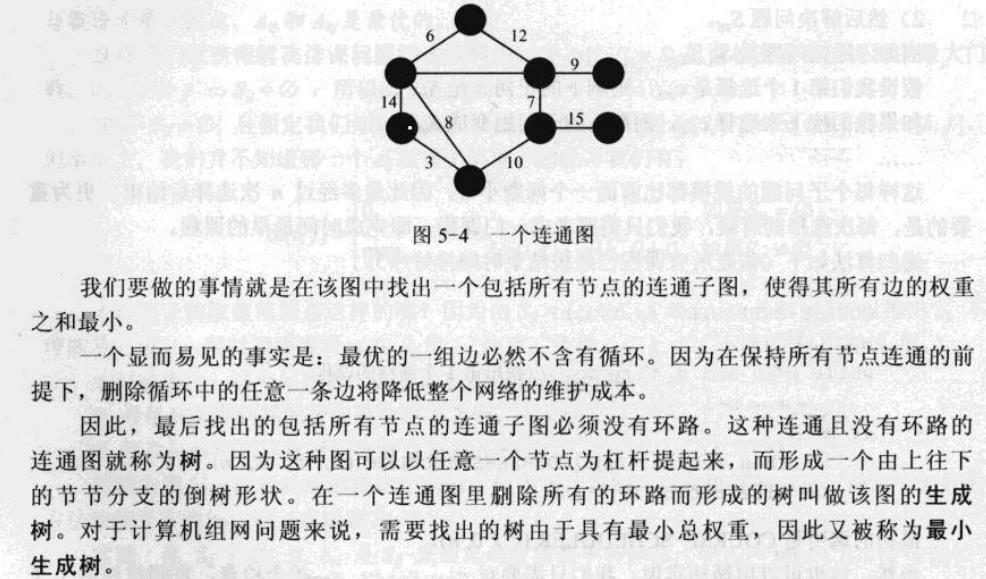
带权无向图 G=(V,E),每条边的权重为wi
1.Prim
代码一:

//手写prim 类似于dijkstra #include<iostream> #include<cstring> using namespace std; const int INF=0x7fffffff; const int maxn=100; int graph[maxn][maxn]; int visit[maxn]; int dist[maxn]; int m,n; int prime(int cur) { int index; int sum = 0; memset(visit, 0, sizeof(visit)); //标记未访问的点 visit[cur] = true;//当前的点入树 for(int i = 0; i < m; i ++){ dist[i] = graph[cur][i]; //dis记录起始点到各个点之间的距离 } for(int i = 1; i < m; i ++){ //从第二个点开始检测 目的是为了找最小权值 int mincost = INF; for(int j = 0; j < m; j ++){//遍历所有点 找最短距离及点 if(!visit[j] && dist[j] < mincost){ mincost = dist[j]; index = j; } } visit[index] = true;//入树操作 sum += mincost; for(int j = 0; j < m; j ++){//更新结点 if(!visit[j] && dist[j] > graph[index][j]){ dist[j] = graph[index][j]; } } } return sum; } int main() { int u,v,l; cin>>m>>n; memset(graph,0x3f,sizeof(graph)); for(int i=0;i<n;i++){ cin>>u>>v>>l; graph[u-1][v-1]=graph[v-1][u-1]=l; } cout<<prime(0); }
代码二:堆实现

//堆实现prim 最小生成树 #include<iostream> #include<cstring> //#include<climits> #include<queue> //堆 #include<algorithm> using namespace std; const int maxn=100; const int M=0x3f3f3f3f; struct graph{ int v; //点 int d;//边 int a[maxn][maxn]; }; graph g; struct edge{ //表示边 int x; int y; int w; bool operator>(const edge &other)const{ return w>other.w; // 从大往小排列 } }; int prim(graph &g){ int sum=0; // cout<<sum<<"heloo"<<endl; priority_queue<edge,vector<edge>,greater <edge> >q; const int n=g.v; bool* used=new bool[n]; std::fill(used,used+n,false);//牛逼 int count=1; int u=0; used[u]=true; // cout<<"ok1"<<endl; while(count<n){ // cout<<"ok2"<<endl; for(int v=0;v<n;v++) if(!used[v]){//若v不在则 u v 加入堆 edge e={u,v,g.a[u][v]}; q.push(e); } while(!q.empty()&&count<n){ const edge e=q.top(); q.pop(); if(!used[e.y]){ sum+=g.a[e.x][e.y]; // cout<<"ok"<<sum<<endl; u=e.y; used[u]=true; count++; break; } } } return sum; } void print(){ int m,n,u,v,l; cin>>m>>n; g.v=m; g.d=n; memset(g.a,0x3f,sizeof(g.a)); for(int i=0;i<n;i++){ cin>>u>>v>>l; g.a[u-1][v-1]=g.a[v-1][u-1]=l; } } int main(){ print(); cout<<prim(g); }
测试数据;

5 6 1 2 5 2 3 5 2 4 12 3 4 17 2 5 15 3 5 6
2.Kraskal算法:一条边一条边地构建最小生成树,除了每次选的边不能与选好的之间产生回路外,只需在剩下的边中选取权重最小的即可

#include <iostream> #include<algorithm> using namespace std; #define MAX 100 struct edge { int x,y; int w; }e[MAX]; int fa[MAX]; int rank[MAX]; int sum; int cmp(edge a,edge b)//排序函数 { if(a.w!=b.w) return a.w<b.w; else { return a.x<b.x; } } void make_set(int x)//初始化节点 { fa[x]=x; rank[x]=0; } int find(int x)//查找父节点 { return fa[x]==x?x:fa[x]=find(fa[x]); } void union_set(int x,int y,int w)//合并节点 { if(rank[x]>rank[y]) { rank[y]=x; } else if(rank[x]<rank[y]) { rank[x]=y; } else { rank[x]++; rank[y]=x; } sum+=w;//总权值加上w } int main() { int x,y,w; int m,n;//n是点,m是边 cin>>n>>m; for(int i=0;i<m;i++) { cin>>x>>y>>w; e[i].x=x; e[i].y=y; e[i].w=w; make_set(x); make_set(y); } sort(e,e+m,cmp); sum=0; for(int i=0;i<n;i++) { x=find(e[i].x); y=find(e[i].y); w=e[i].w; if(x!=y) { union_set(x,y,w); } } cout<<sum<<endl; return 0; }
绝对正确的代码:

//Kruscal #include <stdio.h> #include <string.h> #include <algorithm> #define MAXN 11 //顶点个数的最大值 #define MAXM 20 //边的个数的最大值 using namespace std; struct edge //边 { int u, v, w; //边的顶点、权值 }edges[MAXM]; //边的数组 int parent[MAXN]; //parent[i]为顶点 i 所在集合对应的树中的根结点 int n, m; //顶点个数、边的个数 int i, j; //循环变量 void UFset( ) //初始化 { for( i=1; i<=n; i++ ) parent[i] = -1; } int Find( int x ) //查找并返回节点 x 所属集合的根结点 { int s; //查找位置 for( s=x; parent[s]>=0; s=parent[s] ); while( s!=x ) //优化方案―压缩路径,使后续的查找操作加速。 { int tmp = parent[x]; parent[x] = s; x = tmp; } return s; } //将两个不同集合的元素进行合并,使两个集合中任两个元素都连通 void Union( int R1, int R2 ) { int r1 = Find(R1), r2 = Find(R2); //r1 为 R1 的根结点,r2 为 R2 的根结点 int tmp = parent[r1] + parent[r2]; //两个集合结点个数之和(负数) //如果 R2 所在树结点个数 > R1 所在树结点个数(注意 parent[r1]是负数) if( parent[r1] > parent[r2] ) //优化方案――加权法则 { parent[r1] = r2; parent[r2] = tmp; } else { parent[r2] = r1; parent[r1] = tmp; } } bool cmp( edge a, edge b ) //实现从小到大排序的比较函数 { return a.w <= b.w; } void Kruskal( ) { int sumweight = 0; //生成树的权值 int num = 0; //已选用的边的数目 int u, v; //选用边的两个顶点 UFset( ); //初始化 parent[]数组 for( i=0; i<m; i++ ) { u = edges[i].u; v = edges[i].v; if( Find(u) != Find(v) ) { printf( "%d %d %d\n", u, v, edges[i].w ); sumweight += edges[i].w; num++; Union( u, v ); } if( num>=n-1 ) break; } printf( "weight of MST is %d\n", sumweight ); } int main( ) { int u, v, w; //边的起点和终点及权值 scanf( "%d%d", &n, &m ); //读入顶点个数 n for( int i=0; i<m; i++ ) { scanf( "%d%d%d", &u, &v, &w ); //读入边的起点和终点 edges[i].u = u; edges[i].v = v; edges[i].w = w; } sort(edges,edges+m,cmp); Kruskal(); return 0; }
自我实现代码:

//最小生成树 kruscal 并查集加排序 #include<iostream> #include<algorithm> using namespace std; const int maxn=100; int parent[maxn]; struct node{ int u,v,w; }edge[maxn]; bool cmp(const node &a,const node &b){ return a.w<b.w; } void ufset(int n){ for(int i=0;i<n;i++) parent[i]=-1; } int find(int x){ int p; for(p=x;parent[p]>=0;p=parent[p]); while(p!=x){ int tmp=parent[x]; parent[x]=p; x=tmp; } return p; } void Union(int R1,int R2){ int r1=find(R1); int r2=find(R2); int tmp=parent[r1]+parent[r2]; if(parent[r1]>parent[r2]){ parent[r1]=r2; parent[r2]=tmp; }else { parent[r2]=r1; parent[r1]=tmp; } } void kruscal(int n,int m){ int sum=0; int num=0; int u,v; ufset(n); for(int i=0;i<m;i++){ u=edge[i].u; v=edge[i].v; if(find(u)!=find(v)){ cout<<u<<" "<<v<<" "<<edge[i].w<<endl; sum+=edge[i].w; num++; Union(u,v); } if(num>=n-1) break; } cout<<sum<<endl; } int main() { int m,n; cin>>n>>m; node p; for(int i=0;i<m;i++){ cin>>p.u>>p.v>>p.w; edge[i]=p; } sort(edge,edge+m,cmp); kruscal(n,m); }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号