迭代的是人，递归的是神（第一篇——递归调用的分析）

前言：

迭代的是人，递归的是神。——L. Peter Deutsch

展开递归调用，是分析递归的利器。

进行数学归纳，是使用递归的利器。

对初学者而言，讲一大堆理论，不如举一个例子。

本系列分三篇分析及使用递归。

 

第一篇——递归调用的分析

第二篇——递归调用的初步使用

第三篇——递归调用的进阶使用

 

一、递归调用的一般结构。

递归函数一般有如下特征：

recursionFun()

{

     //第一部分：递归结束条件，前期处理。

     if 递归结束条件

         return;

     //第二部分：递归调用。

     recusionFun();

     //第三部分：递归调用后期处理，也可能有return语句。

}

 

二、递归调用的4种形式。

下面看递归调用的4种形式：

1、

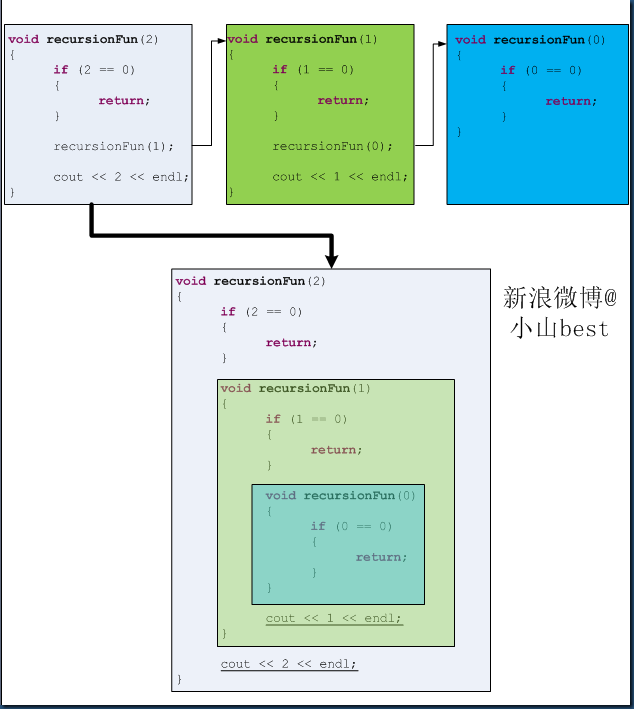
void recursionFun(int n)
{
	if (n == 0)
	{
		return;
	}

	cout << n;

	recursionFun(n - 1);
}

recursionFun(3)输出321.

 

 

2、

void recursionFun(int n)
{
	if (n == 0)
	{
		return;
	}

	recursionFun(n - 1);

        cout << n; 

}

recursionFun(3)输出123.

 

 

3、

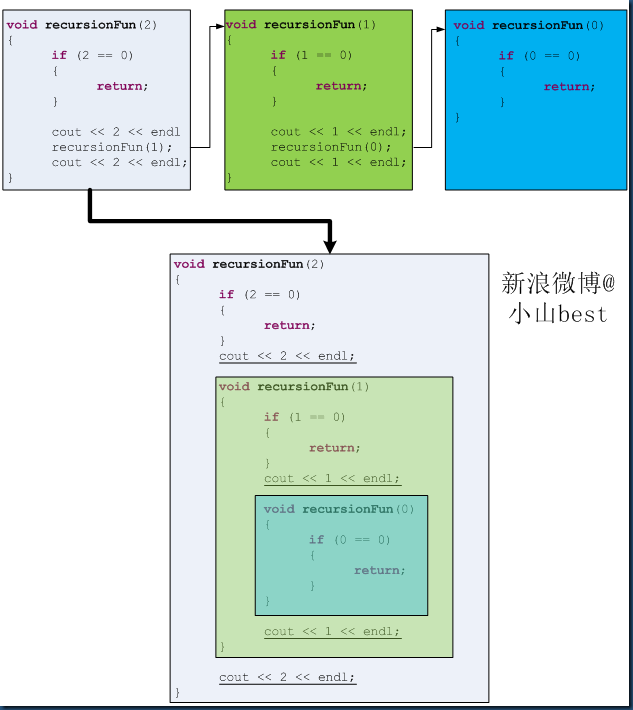
void recursionFun(int n)
{
	if (n == 0)
	{
		return;
	}

	cout << n;

	recursionFun(n - 1);

	cout << n;
}

recursionFun(3)输出321123.

 

 

4、

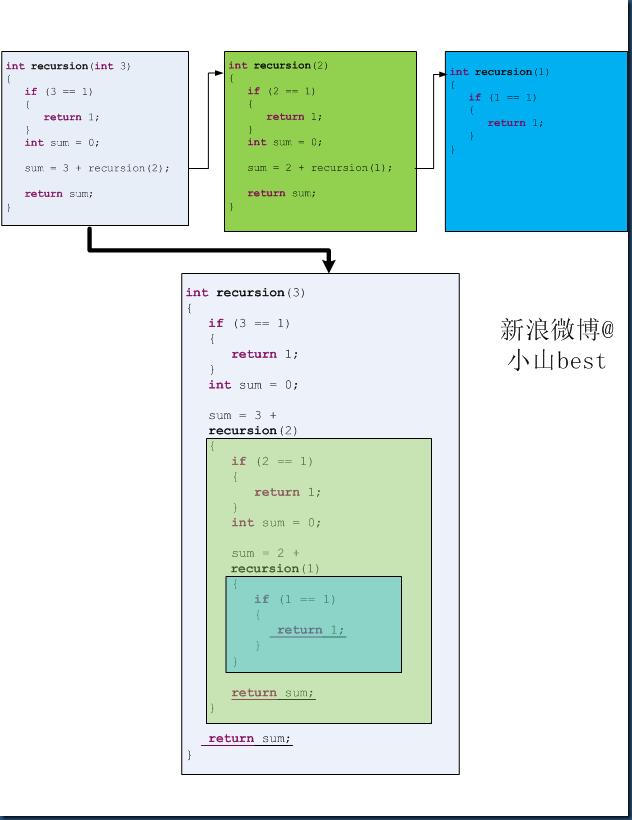
int recursionFun(int n)
{
	if (n == 1)
	{
		return 1;
	}
	int sum = 0;

	sum = n + recursion(n - 1);

	return sum;
}

recursionFun(3)输出6.

 

二、第1种形式的分析。

这里为了简便以recursionFun(2)为例。

void recursionFun(int n)
{
	if (n == 0)
	{
		return;
	}

	cout << n;

	recursionFun(n - 1);
}

 

记住，把递归调用展开分析！如下图。

   

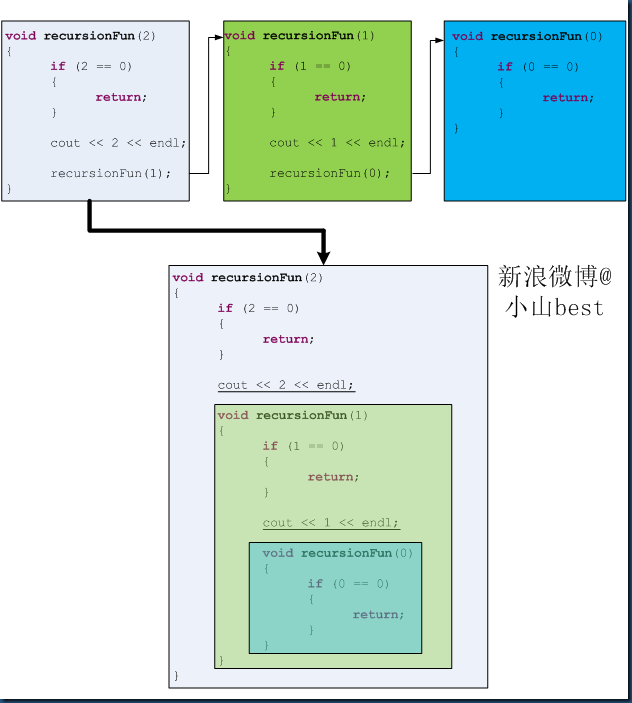
三、第2种形式的分析。

 

 

void recursionFun(int n)
{
	if (n == 0)
	{
		return;
	}

	recursionFun(n - 1);

        cout << n; 
}

 

 

 

四、第3种形式的分析。

void recursionFun(int n)
{
	if (n == 0)
	{
		return;
	}

	cout << n;

	recursionFun(n - 1);

	cout << n;
}

 

 

 

五、第4种形式的分析。

int recursionFun(int n)
{
	if (n == 1)
	{
		return 1;
	}
	int sum = 0;

	sum = n + recursion(n - 1);

	return sum;
}