「csp模拟」模拟测试4

* T1是暴力分，T2当时没有花太多时间去推导，一见到T2就十分害怕，便放过了它，T3的话花了大量的时间推了一个错误的解，，， * 以后对于T2这种题不要未战先怯，一点一点的去推导！

那一天我们许下约定

题目描述

那一天我们在教室里许下约定。
我至今还记得我们许下约定时的欢声笑语。我记得她说过她喜欢吃饼干，很在意自己体重的同时又控制不住自己。她跟我做好了约定：我拿走她所有的饼干共\(\text N\)块，在从今天起不超过\(\text D\)天的时间里把所有的饼干分次给她，每天给她的饼干数要少于\(\text M\)以防止她吃太多。
当然，我们的约定并不是饼干的约定，而是一些不可言状之物。
现今回想这些，我突然想知道，有多少种方案来把饼干分给我的她。

输入格式

每个测试点有多组测试数据。数据组数 \(\text T \le \text 10\)
对于每组数据，有一行共三个整数 \(\text {N,D,M}\) 含义如题。
输入结束标识为 \(\text {"0 0 0"}\) (不含引号)。

输出格式

对于每组数据，输出一行共一个整数，表示方案数对 998244353 取模后的结果。

样例

样例输入

样例输出

题解

一眼 \(\text{O(nmd)}\) 简单dp，考虑如何优化
因为D的范围远大于N和M，所以在dp中会出现很多一个饼干都不给的天数，于是就变换状态定义，dp出用i的有效天分完n个饼干的方案数，然后把这i个有效天分布在d天中就行了。
公式如下所示：

\[ans = \sum dp(i, 0) \times \binom{d}{i} \]

code

#include <bits/stdc++.h>
using namespace std;
//#define int long long
#define print(x) cerr << #x << " : " << x << endl;
inline int read() {
    int k = 0, f = 1; char ch = getchar();
    for (; !isdigit(ch); ch = getchar()) if (ch == '-') f = -1;
    for (; isdigit(ch); ch = getchar()) k = k * 10 + ch - '0';
    return k * f;
}
const int mod = 998244353;
const int maxn = 2000 + 10;
long long n, m, d;
long long f[maxn][maxn], sum[maxn][maxn], C[maxn];
long long jc[maxn], ny[maxn], jcny[maxn];
signed main () {
#ifdef local
    freopen("in", "r", stdin);    
#else
    freopen("contract.in", "r", stdin);
    freopen("contract.out", "w", stdout);
#endif
    jc[0] = 1, ny[1] = 1, jcny[1] = 1;
    for (int i = 1; i <= 2000; i++) jc[i] = jc[i - 1] * i % mod;
    for (int i = 2; i <= 2000; i++) ny[i] = (mod - mod / i) * ny[mod % i] % mod;
    for (int i = 2; i <= 2000; i++) jcny[i] = jcny[i - 1] * ny[i] % mod;
    while(scanf("%lld%lld%lld", &n, &d, &m)) {
        d %= mod;
        if (!n && !d && !m) return 0;
        C[1] = d % mod;
        for (int i = 2; i <= n; i++) C[i] = C[i - 1] * (d - i + 1) % mod;
        memset(f, 0, sizeof(f));
        memset(sum, 0, sizeof(sum));
        for (int i = 0; i <= n; i++) sum[0][i] = 1;
        f[0][0] = 1;
        long long ans = 0;
        for (int i = 1; i <= (n > d ? d : n); i++) {
            for (int j = 1; j <= n; j++) {
                if (j - m + 1 > 0) f[i][j] = (sum[i - 1][j - 1] - sum[i - 1][j - m] + mod) % mod;
                else f[i][j] = sum[i - 1][j - 1] % mod;
                sum[i][j] = (sum[i][j - 1] + f[i][j]) % mod;
            }
            ans = (ans + f[i][n] * jcny[i] % mod * C[i] % mod) % mod;
        }
        printf("%lld\n", ans);
    }
}

题(problem)

题目描述

出个题就好了.这就是出题人没有写题目背景的原因.
你在平面直角坐标系上.
你一开始位于(0,0).
每次可以在上/下/左/右四个方向中选一个走一步.
即:从(x,y)走到(x,y+1),(x,y-1),(x-1,y),(x+1,y)四个位置中的其中一个.
允许你走的步数已经确定为n.现在你想走n步之后回到(0,0).但这太简单了.你希望知道有多少种不同的方案能够使你在n步之后回到(0,0).当且仅当两种方案至少有一步走的方向不同,这两种方案被认为是不同的.
答案可能很大所以只需要输出答案对10^{9+7取模后的结果.(10}9+7=1000000007,1和7之间有8个0)
这还是太简单了,所以你给能够到达的格点加上了一些限制.一共有三种限制,加上没有限制的情况,一共有四种情况,用0,1,2,3标号:
0.没有任何限制,可以到达坐标系上所有的点,即能到达的点集为{(x,y)|x,y为整数}
1.只允许到达x轴非负半轴上的点.即能到达的点集为{(x,y)|x为非负数,y=0}
2.只允许到达坐标轴上的点.即能到达的点集为{(x,y)|x=0或y=0}
3.只允许到达x轴非负半轴上的点,y轴非负半轴上的点以及第1象限的点.即能到达的点集为{(x,y)|x>=0,y>=0}

输入格式

一行两个整数(空格隔开)n和typ,分别表示你必须恰好走的步数和限制的种类.typ的含义见【题目描述】.

输出格式

一行一个整数ans,表示不同的方案数对10^9+7取模后的结果.

样例

样例输入

【样例输入0】
100 0
【样例输出0】
383726909
【样例输入1】
100 1
【样例输出1】
265470434
【样例输入2】
100 2
【样例输出2】
376611634
【样例输入3】
100 3
【样例输出3】
627595255

样例输出

数据范围与提示

10%的数据,typ=0,n<=100
10%的数据,typ=0,n<=1000
5%的数据, typ=0,n<=100000
10%的数据,typ=1,n<=100
10%的数据,typ=1,n<=1000
5%的数据, typ=1,n<=100000
10%的数据,typ=2,n<=100
15%的数据,typ=2,n<=1000
10%的数据,typ=3,n<=100
10%的数据,typ=3,n<=1000
5%的数据, typ=3,n<=100000
以上11部分数据没有交集.
100%的数据,保证n为偶数,2<=n<=100000,0<=typ<=3.

题解

情况0 ：

\[\\ \because l = r, u = d \\ \because l + r + u + d = n \\ \therefore \sum \frac{n!}{l! \times r! \times u! \times d! } \]

对于每一个l计算即可。

情况1 ：卡特兰数
情况2 ： \(\text{O}(n^2) dp\) 即可。
情况3 ：枚举向上移动的步数，答案就是该步数的组合数和两个卡特兰数的乘积，求和即可。

code

//这个代码写的有点复杂了，可以将卡特兰数写成函数的形式，方便很多！～
#include <bits/stdc++.h>
using namespace std;
#define print(x) cerr << #x << " : " << x << endl;
#define int long long
inline int read() {
    int k = 0, f = 1; char ch = getchar();
    for (; !isdigit(ch); ch = getchar()) if (ch == '-') f = -1;
    for (; isdigit(ch); ch = getchar()) k = k * 10 + ch - '0';
    return k * f;
}
const int mod = 1e9 + 7;
const int maxn = 8000000 + 100;
int jc[maxn];
int qpow(int x, int y) {
    int ans = 1;
    for (; y; y >>= 1, x = x * x % mod) if (y & 1) ans = ans * x % mod;
    return ans % mod;
}
int C(int n, int m) { return jc[n] * qpow(jc[m], mod - 2) % mod * qpow(jc[n - m], mod - 2) % mod; }
int dp[maxn];
signed main () {
#ifdef local
    freopen("in", "r", stdin);    
#else
    freopen("problem.in", "r", stdin);
    freopen("problem.out", "w", stdout);
#endif
    int n = read(), opt = read();
    jc[0] = 1;
    for (int i = 1; i <= 2 * n; i++) jc[i] = jc[i - 1] * i % mod;
    if (opt == 0) {
        int ans = 0;
        for (int i = 1; i < n / 2; i++) {
            ans = (ans + jc[n] * qpow(jc[i], mod - 2) % mod * qpow(jc[n / 2 - i], mod - 2) % mod * qpow(jc[i], mod - 2) % mod * qpow(jc[n / 2 - i], mod - 2)) % mod;
            ans %= mod;
        }
        ans = (ans + jc[n] * qpow(jc[n / 2], mod - 2) % mod * qpow(jc[n / 2], mod - 2) % mod) % mod;
        ans = (ans + jc[n] * qpow(jc[n / 2], mod - 2) % mod * qpow(jc[n / 2], mod - 2) % mod) % mod;
        cout << ans << endl;    
    } else if (opt == 1) {
        cout << (C(n, n / 2) - C(n, n / 2 - 1) + mod) % mod << endl;
    } else if (opt == 2) {
        dp[0] = 1; dp[2] = 4;
        for(int i = 4; i <= n; i+=2)
            for(int j = 2; j <= i; j += 2)
                dp[i] = (dp[i] + (C(j - 2, j / 2 - 1) - C(j - 2, j / 2 - 2) + mod) % mod * 4 % mod * dp[i - j] % mod) % mod;    
        cout << dp[n] << endl;
    } else if (opt == 3) {
        int ans = 0;
        for(int i = 0; i <= n; i += 2) 
            ans = (ans + C(n, i) * (C(i, i / 2) - C(i, i / 2 - 1) + mod) % mod * (C(n - i, (n - i) / 2) - C(n - i, (n - i) / 2 - 1) + mod) % mod) % mod;   
        cout << ans << endl;
    }
    return 0;    
}

寿司

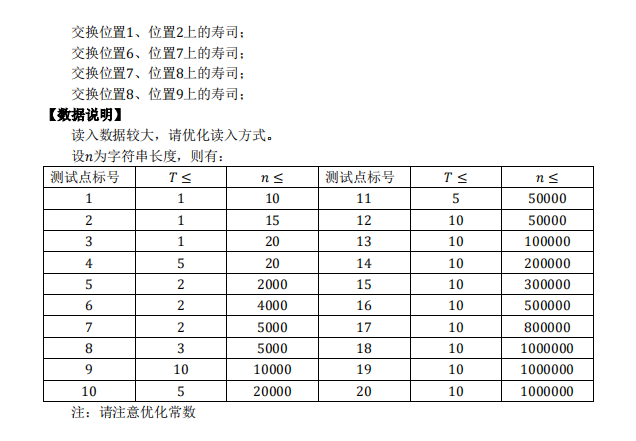
题解

断环成链，移动B和移动R的情况一样，假设移动B,枚举每个链上的每个B点到两个端点的移动次数（就是距离-其中B的个数），取min，然后加和。这是40分做法。
考虑优化，自行理解。。。

code

40分代码


#include 
using namespace std;
#define min(a, b) (a) < (b) ? (a) : (b)
#define print(x) cerr << #x << " : " << x << endl;
#define PRINT(x, size) copy(x + 1, x + size + 1, ostream_iterator(cout, " ")), cout << endl;
inline int read() {
    int k = 0, f = 1; char ch = getchar();
    for (; !isdigit(ch); ch = getchar()) if (ch == '-') f = -1;
    for (; isdigit(ch); ch = getchar()) k = k * 10 + ch - '0';
    return k * f;
}
const int maxn = 20000 + 100;
char s[maxn];
int a[maxn], sum[maxn];
int main () {
#ifndef local
    freopen("sushi.in", "r", stdin);
    freopen("sushi.out", "w", stdout);
#endif
    int T = read();
    while (T--) {
        scanf("%s", s + 1);
        int n = strlen(s + 1);
        copy(s + 1, s + n + 1, s + n + 1);
//      copy(s + 1, s + n + n + 1, ostream_iterator(cout, " "    ));
        sum[0] = 0;
        for (int i = 1; i <= n + n; i++) a[i] = (s[i] == 'B' ? 1 : 0);
        for (int i = 1; i <= n + n; i++) sum[i] = sum[i - 1] + a[i];
//      PRINT(a, 2 * n); PRINT(sum, 2 * n)
        long long ans = 0x3f3f3f3f3f3f3f;
        for (int j = 1; j <= n; j++) {
            int ans1 = 0;
            for (int i = j; i <= n + j - 1; i++) {
                if (a[i] == 0) ans1 += min(sum[i - 1] - sum[j - 1], sum[j + n - 1] - sum[i]);
            }
            ans = min(ans1, ans);
        }
        printf("%lld\n", ans);
    }
}

满分代码在路上！

posted @ 2020-10-02 11:31 hyskr 阅读(190) 评论(0) 编辑收藏举报

刷新页面返回顶部

Cosmic

若能避开猛烈的欢喜，自然也不会有悲痛的来袭。 ---《人间失格》

「csp模拟」模拟测试4

那一天我们许下约定

题目描述

输入格式

输出格式

样例

样例输入

样例输出

题解

code

题(problem)

题目描述

输入格式

输出格式

样例

样例输入

样例输出

数据范围与提示

题解

code

寿司

题解

code

公告