十字绣

题目描述

考古学家发现了一块布，布上做有针线活，叫做“十字绣”，即交替地在布的两面穿线。

布是一个\(n*m\)的网格，线只能在网格的顶点处才能从布的一面穿到另一面。每一段线都覆盖一个单位网格的两条对角线之一，而在绣的过程中，一针中连续的两段线必须分处布的两面。并且每一段线只能走一次。

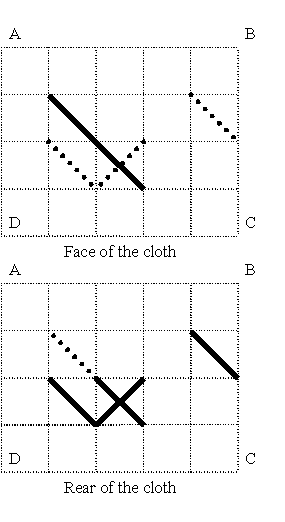
给出布两面的图案，问最少需要几针才能绣出来？一针是指针不离开布的一次绣花过程。

输入格式

第1行两个数\(N\)和\(M\)。

接下来\(N\)行每行\(M\)个数描述正面。

再接下来\(N\)行每行\(M\)个数描述反面。

每个格子用.（表示空）,\(/\)（表示从右上角连到左下角）,\(\$（表示从左上角连到右下角）和\)X$（表示连两条对角线）表示。

输出格式

一个数，最少要用的针数。

样例

样例输入

4 5
.....
.\...
..\..
.....
.....
....\ 
.\X..
.....

样例输出

4

数据范围与提示

对于100%的数据，\(1<=n,m<=200\)

题解

• 首先，考虑能够一针解决的，肯定是在一个针线两端相连的连通块里，这种情况下把所有连通块里的针数相加即可。

• 这里求连通块用dfs或者并查集即可。由于是二维坐标，还是转换成一维的点的编号比较方便。
  下面我们就可以把原图转换成一个无向图，求连通块数。

• 每个连通块里的真数怎么求？

• 针的穿入穿出是在结点的位置，对于某一个结点：

  • 如果既有一条正面的线，也有一条反面的线，对于该结点我们可以把它当做一针；
  • 如果有两条正面的线，一条反面的线，那么对于该结点至少需要两针才能搞定；
  • 我们扩展到一个连通块，每个结点都会有对应的最少针数，即为正面反面线数量的差绝对值。
  • 我们可以累加起来，但是由于每一条线对应两个端点，因此一条线会对两个端点的针数做贡献，所以我们最后将总和除以2。
  • 特别的，如果总和为0，我们可以认为是出现了一个环形的结构，即一针搞定，所以针数是加1.

code

#include <bits/stdc++.h>
using namespace std;
const int maxn = 200 + 10;
char c[maxn];
int s, n, m;
int h[maxn][maxn];
struct node {
    int t, next;
} e[maxn * maxn * 8];
int head[maxn * maxn], f[maxn * maxn], jl[maxn * maxn];
int near[maxn * maxn];
int v[maxn * maxn];
int tot = 0;
void add(int x, int y, int z) {
    f[x] = 1;
    e[++tot] = (node){ y, head[x] };
    head[x] = tot;
    if (z == 1)
        jl[x]++;
    else
        near[x]++;
}
void add1(int x, int y, int k) {
    add(h[x][y + 1], h[x + 1][y], k);
    add(h[x + 1][y], h[x][y + 1], k);
}
void add2(int x, int y, int k) {
    add(h[x][y], h[x + 1][y + 1], k);
    add(h[x + 1][y + 1], h[x][y], k);
}
void read(int k) {
    for (int i = 1; i <= n; i++) {
        scanf("%s", c + 1);
        for (int j = 1; j <= m; j++)
            if (c[j] == 'X')
                add1(i, j, k), add2(i, j, k);
            else if (c[j] == '/')
                add1(i, j, k);
            else if (c[j] == '\\')
                add2(i, j, k);
    }
}
void dfs(int x) {
    v[x] = 1;
    s += abs(jl[x] - near[x]);
    for (int i = head[x]; i; i = e[i].next)
        if (!v[e[i].t])
            dfs(e[i].t);
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n + 1; i++)
        for (int j = 1; j <= m + 1; j++) h[i][j] = (i - 1) * (m + 1) + j;
    read(1);
    read(-1);
    int ans = 0;
    for (int i = 1; i <= n + 1; i++)
        for (int j = 1; j <= m + 1; j++) {
            int x = h[i][j];
            if (!f[x] || v[x])
                continue;
            s = 0;
            dfs(x);
            if (s == 0)
                s = 1;
            else if (s != 0)
                s = s / 2;
            ans += s;
        }
    cout << ans;
    return 0;
}

#include <bits/stdc++.h>
using namespace std;
inline int read() {
    int k = 0, f = 1; char ch = getchar();
    for (; !isdigit(ch); ch = getchar()) if(ch == '-') f = -1;
    for (; isdigit(ch); ch = getchar()) k = k * 10 + ch - '0';
    return k * f;
}
const int maxn = 401;
struct node { int to, next; } e[maxn * maxn * 8];
int head[maxn * maxn], ecnt;
int face[maxn * maxn], rear[maxn * maxn], jl[maxn * maxn];
void add(int u, int v, int w) {
    jl[u] = 1;
    e[++ecnt]= (node){v, head[u]}, head[u] = ecnt;
    w == 1 ? face[u]++ : rear[u]++;
}
int id[maxn][maxn];
void add1(int x, int y, int k) {
// 从右上到左下建边
    add(id[x][y + 1], id[x + 1][y], k);
    add(id[x + 1][y], id[x][y + 1], k);
}
void add2(int x, int y, int k) {
// 从左上到右下建边
    add(id[x][y], id[x + 1][y + 1], k);
    add(id[x + 1][y + 1], id[x][y], k);
}
int vis[maxn * maxn], now = 0;
void dfs(int x) {
    vis[x] = 1;
    now += abs(face[x] - rear[x]);
    for (int i = head[x]; i; i = e[i].next) {
        int v = e[i].to;
        if (vis[v]) continue;
        dfs(v);
    }
}
int main() {
#ifdef debug
    //freopen("stitch.in", "r", stdin);
#else 
    freopen("stitch.in", "r", stdin);
    freopen("stitch.out", "w", stdout);
#endif
    int n = read(), m = read();
    for (int i = 1; i <= n + 1; i++)
        for (int j = 1; j <= m + 1; j++)
            id[i][j] = (i - 1) * (m + 1) + j;
    
    for (int i = 1; i <= n; i++) {
        char s[maxn]; scanf("%s", s + 1);
        for (int j = 1; j <= m; j++) {
            if (s[j] == '.') continue;
            else if (s[j] == '\\') add2(i, j, 1);
            else if (s[j] == '/') add1(i, j, 1);
            else add1(i, j, 1), add2(i, j, 1);
        }
    }
    for (int i = 1; i <= n; i++) {
        char s[maxn]; scanf("%s", s + 1);
        for (int j = 1; j <= m; j++) {
            if (s[j] == '.') continue;
            else if (s[j] == '\\') add2(i, j, -1);
            else if (s[j] == '/') add1(i, j, -1);
            else add1(i, j, -1), add2(i, j, -1);
        }
    }
    int ans = 0;
    for (int i = 1; i <= n + 1; i++)
        for (int j = 1; j <= m + 1; j++) {
            int cur = id[i][j];
            if (jl[cur] == 0 || vis[cur]) continue;
            now = 0;
            dfs(cur);
            ans += (now == 0) ? 1 : (now / 2);
        }
    printf("%d\n", ans);
    return 0;
}