方格取数

    <h2 class="ui header">题目描述</h2>
    <div class="font-content" id="pv-description"><div style="position: relative; overflow: hidden; "><p>设有N*N的方格图(N&lt;=20,我们将其中的某些方格中填入正整数,而其他的方格中则放入数字0。如下图所示(见样例)：</p>

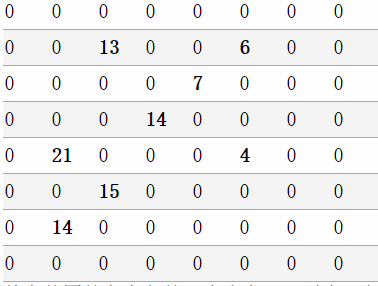
某人从图的左上角的A(1,1) 点出发，可以向下行走，也可以向右走，直到到达右下角的B(n,n)点。在走过的路上（包括起点在内），他可以取走方格中的数(取走后的方格中将变为数字0)。此人从A点到B 点共走两次，试找出2条这样的路径，使得取得的数之和为最大。

输入格式

输入的第一行为一个整数N(表示N*N的方格图)

接下来的每行有三个整数，前两个表示位置，第三个数为该位置上所放的数。一行单独的0表示输入结束。

输出格式

只需输出一个整数，表示2条路径上取得的最大的和

样例

样例输入

8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0

样例输出

67

题解

• 只能从左边和上面转移过来，\(fx[i][j-1]\)和\(fx[i-1][j]\) 与 \(fy[i][j-1]\)和\(fy[i-1][j]\)排列组合，求最大值
• 即为 \(f[i][j-1][k-1][l]\) , \(f[i][j-1][k][l-1]\) , \(f[i-1][j][k-1][l]\) , \(f[i-1][j][k][l-1]\)
• 然后判断是否选择了同一个方格
• 如果是只加一遍
• 不是的话加两个方格的

code

#include <bits/stdc++.h>
using namespace std;
//只能从左边和上面转移过来，fx[i][j-1]和fx[i-1][j] 与 fy[i][j-1]和fy[i-1][j]排列组合，求最大值
//即为 f[i][j-1][k-1][l] , f[i][j-1][k][l-1] , f[i-1][j][k-1][l] , f[i-1][j][k][l-1]
//然后判断是否选择了同一个方格
//如果是只加一遍
//不是的话加两个方格的
const int maxn = 25;
int map_[maxn][maxn], f[maxn][maxn][maxn][maxn];
int main() {
    int n;
    cin >> n;
    int x, y, z;
    int cnt = 0;
    while (cin >> x >> y >> z && x && y && z) {
        map_[x][y] = z;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                for (int k = 1; k <= n; k++) {
                    for (int l = 1; l <= n; l++) {
                        f[i][j][k][l] = max(
                            f[i][j - 1][k - 1][l],
                            max(f[i][j - 1][k][l - 1], max(f[i - 1][j][k - 1][l], f[i - 1][j][k][l - 1])));
                        if (i == k && j == l)  //如果选择了同一个方格只能加一遍
                            f[i][j][k][l] += map_[i][j];
                        else  //加两个方格的
                            f[i][j][k][l] += map_[i][j] + map_[k][l];
                    }
                }
            }
        }
    }
    cout << f[n][n][n][n];
    return 0;
}