树链剖分学习笔记

概念

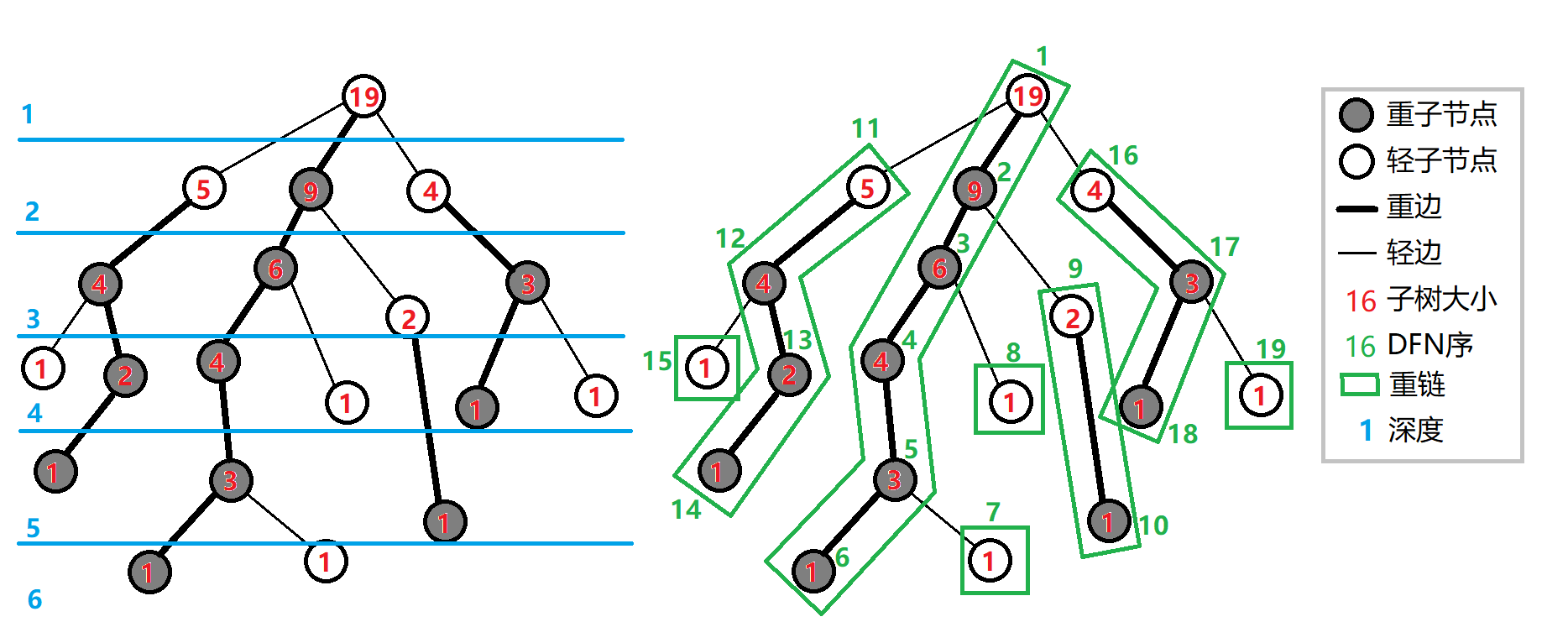
• 重子节点：表示其子节点中子树（即size[]最大）最大的子结点。如果有多个子树最大的子结点，取其一。如果没有子节点，就无重子节点。

• 轻子节点：表示剩余的所有子结点。

• 重边：父亲结点和重子节点连成的边。

• 轻边：父亲节点和轻子节点连成的边。

• 重链：若干条首尾衔接的重边构成。

• 轻链：由多条轻边连接而成的路径。

• 把落单的结点也当作重链。

• 叶节点没有重儿子，非叶节点有且只有一个重儿子。

• 上一经典图片：

原理：

• 树剖的实现分两个 DFS 的过程。

第一个 DFS

• 记录每个结点的父节点（f）、深度（deep）、子树大小（size）、重子节点（son）。

解释：

• size数组为子树大小，由于这个子树包含自己，所以初始化为1
• deep数组为深度，rt节点的深度deep[rt]就是他父亲节点的深度+1，即\(deep[rt]=deep[fa]+1\);
• f数组记录父亲节点，即f[rt]=fa;
• 然后遍历；
• 然后层次深度+1，并用子节点的size[]来更新父节点的size[]；
• 最后，选取size最大的作为重儿子；

code

void dfs(int rt, int fa) {
    size[rt] = 1;//size[]数组为子树大小，由于这个子树包含自己，所以初始化为1
    deep[rt] = deep[fa] + 1;//deep[]数组为深度，rt节点的深度deep[rt]就是他父亲节点的深度+1，即deep[rt]=deep[fa]+1;
    f[rt] = fa;//f[]数组记录父亲节点，即f[rt]=fa;
    for (int x = head[rt]; x; x = edges[x].next) {//遍历
        if (edges[x].to == fa)
            continue;
        dfs(edges[x].to, rt);//层次深度+1
        size[rt] += size[edges[x].to];//用子节点的size[]来更新父节点的size[]
        if (size[son[rt]] < size[edges[x].to])//选取size最大的作为重儿子
            son[rt] = edges[x].to;
    }
}

第二个 DFS

• 记录所在链的链顶（top，应初始化为结点本身）,连接重链。

解释

• rt为当前节点，rttop为重链顶端。
• 首先，保存当前节点所在链的顶端节点；
• 然后，先走重儿子，这里如果一个点和它的重儿子处于同一条重链，那么重儿子所在重链的顶端还是rttop；
• 然后，遍历轻链；

code

void dfs2(int rt, int rttop) {//rt为当前节点，rttop为重链顶端。
    top[rt] = rttop;//保存当前节点所在链的顶端节点
    if (son[rt])//先走重儿子
        dfs2(son[rt], rttop);
    for (int x = head[rt]; x; x = edges[x].next)//遍历轻链
        if (edges[x].to != f[rt] && edges[x].to != son[rt])
            dfs2(edges[x].to, edges[x].to);//如果一个点为轻链底端，那么他的top值为它本身。
}

树链剖分lca

解释

• 如果节点u,v不在同一个重链，让深度大的链顶节点u往上跳，跳到其链顶的父亲节点上，即u=f[top[u]]；
• 重复上述步骤直到节点u,v在同一个重链；
• 如果u,v在同一个重链上，即top[u]==top[v]，则深度小的为lca

code

int lca(int u, int v) {
    while (top[u] != top[v]) {
    //如果节点u,v不在同一个重链，让深度大的链顶节点u往上跳，跳到其链顶的父亲节点上，即u=f[top[u]]
        if (deep[top[u]] < deep[top[v]])
            v = f[top[v]];
        else
            u = f[top[u]];
    }
    //重复上述步骤直到节点u,v在同一个重链
    return deep[u] < deep[v] ? u : v;
    //如果u,v在同一个重链上，即，top[u]==top[v]，则深度小的为LCA
}

例题

例题：luogu P3379 树链剖分求LCA

ACcode

#include <bits/stdc++.h>
struct Edge {
    int to, next;
} edges[1000005];
int head[500005], tot, deep[500005], f[500005], son[500005], top[500005], size[500005];
void add(int x, int y) { edges[++tot] = (Edge){ y, head[x] }, head[x] = tot; }
void dfs(int rt, int fa) {
    size[rt] = 1;
    deep[rt] = deep[fa] + 1;
    f[rt] = fa;
    for (int x = head[rt]; x; x = edges[x].next) {
        if (edges[x].to == fa)
            continue;
        dfs(edges[x].to, rt);
        size[rt] += size[edges[x].to];
        if (size[son[rt]] < size[edges[x].to])
            son[rt] = edges[x].to;
    }
}
void dfs2(int rt, int rttop) {
    top[rt] = rttop;
    if (son[rt])
        dfs2(son[rt], rttop);
    for (int x = head[rt]; x; x = edges[x].next)
        if (edges[x].to != f[rt] && edges[x].to != son[rt])
            dfs2(edges[x].to, edges[x].to);
}
int lca(int u, int v) {
    while (top[u] != top[v]) {
        if (deep[top[u]] < deep[top[v]])
            v = f[top[v]];
        else
            u = f[top[u]];
    }
    return deep[u] < deep[v] ? u : v;
}
int main() {
    int n, m, s, a, b;
    scanf("%d%d%d", &n, &m, &s);
    for (int i = 1; i < n; i++) {
        scanf("%d%d", &a, &b);
        add(a, b);
        add(b, a);
    }
    dfs(s, 0);
    dfs2(s, s);
    for (int i = 1; i <= m; i++) {
        scanf("%d%d", &a, &b);
        printf("%d\n", lca(a, b));
    }
    return 0;
}