广告印刷

说明

最近，afy决定给TOJ印刷广告，广告牌是刷在城市的建筑物上的，城市里有紧靠着的N个建筑。afy决定在上面找一块尽可能大的矩形放置广告牌。我们假设每个建筑物都有一个高度，

我们假设每个建筑物都有一个高度，从左到右给出每个建筑物的高度\(H_1,H_2…H_N\)，且\(0<H_i\leqslant10^8\)，并且我们假设每个建筑物的宽度均为1。要求输出广告牌的最大面积。

要求输出广告牌的最大面积。

输入格式

第一行：一个数n (\(n\leqslant 1000\))。

第二行：n个数,给出这n个建筑物。

输出格式

第一行：一个数ans，表示最大面积。

样例

输入样例

6
5 8 4 4 8 4

输出样例

24

解析

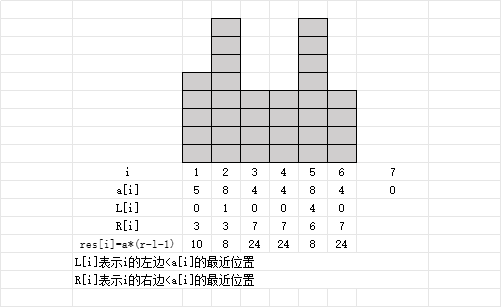
对于每个元素 a[i] 只需要查询其左边<a[i]的最近位置L，右边<a[i]的最近位置R，那么（R-L-1）就是矩形宽度，其面积 \(res=a[i]*(R-L-1)\)。

可以使用暴力求出L,R ，整体复杂度 O(n^2)；

由于L,R是左边<a[i]的最近位置，可以利用单调栈来求得。

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int n,m,a[N],st[N],l[N],r[N];

int main1() {
    cin>>n;
    for(int i=1; i<=n; i++) cin>>a[i];
    int ans=0;
    for(int i=1; i<=n; i++) {
        int l=i,r=i;
        while(l>=1 && a[l] >= a[i]) l--; // a[l] < a[i]
        while(r<=n && a[r] >= a[i]) r++; // a[r] < a[i]
        ans = max(ans, a[i]*(r-l-1));
    }
    cout<<ans<<endl;
    return 0;
}

int main() {
    cin>>n;
    for(int i=1; i<=n; i++) cin>>a[i];
    int hh=0; st[0] = 0;
    for(int i=1; i<=n; i++) {
        while(hh && a[st[hh]] >= a[i]) --hh; // 维护单调递增栈
        l[i] = st[hh];   // 左边最近的 < a[i] 的位置
        st[++hh] = i;    // 入栈
    }
    hh=0, st[hh]=n+1;
    for(int i=n; i>=1; i--) {
        while(hh && a[st[hh]] >= a[i]) --hh; // 维护单调递增栈
        r[i] = st[hh];   // 右边最近的 < a[i] 的位置
        st[++hh] = i;    // 入栈
    }
    long long ans=0;
    for(int i=1; i<=n; i++)
        ans = max(ans, 1ll*a[i] * (r[i]-l[i]-1));
    cout<<ans;
    return 0;
}