CSP2022 J2参考解析
题号为洛谷题号,直接搜索 2022CSP 即可。
P8813 [CSP-J2022] 乘方
-
设计知识点:循环,快速幂
-
题目描述很简单,求 \(a^b\),但是数据范围很大, \(a,b \in [1,10^9]\)。
-
方法1:一眼 long long 快速幂,可AC,但是有一个细节
-
快速幂可能存在情况 ans 合理,ans*a 越界到 \([1,10^9]\),这个坑需要注意。
-
方法2:细想一下 \(a=10^9, a^2=10^{18}\),其实直接暴力枚举就行。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10, INF = 0x3f3f3f3f, M = 1e9;
LL fpow(LL a, LL n) {
LL ans = 1;
while (n) {
if (n & 1) ans = ans * a;
if (ans > M || a > M) return -1;
a = a * a;
n >>= 1;
}
return ans;
}
LL slove2(LL a, LL n) {
LL ans = 1;
for (int i = 1; i <= n; i++) {
ans = ans * a;
if (ans > M) return -1;
}
return ans;
}
int main() {
freopen("pow.in", "r", stdin);
freopen("pow.out", "w", stdout);
LL a, b;
while (cin >> a >> b) {
// cout << fpow(a, b) << endl;
cout << slove2(a, b) << endl;
}
fclose(stdin), fclose(stdout);
return 0;
}
P8814 [CSP-J2022] 解密
-
设计知识点:数学,一元二次方程,二分
-
题意:\(p*q=n, e*d=(p-1)(q-1)+1\),已知 \(n,e,d\),求 \(p,q\)。
-
方法1 数学推导
已知 \(pq=n, p+q=m\),求 \(p,q\)。
\((p+q)^2=p^2+q^2+2pq\)
\((p-q)^2=p^2+q^2-2pq\)
两式相减,可得 \((p+q)^2 - (p-q)^2 = 4pq\),即 \(m^2 - (p-q)^2 = 4n\)
∴ \(|p-q| = \sqrt{m^2-4n}\)
∵ \(p+q=m,p≤q\)
∴\(p=\frac{m - \sqrt{m^2-4n}}{2},q=\frac{m+ \sqrt{m^2-4n}}{2}\)
-
方法2:(其实就是方法1的归纳)明显可以用一元二次方程 \(O(1)\) 解
-
一元二次方程:\(ax^2+bx+c=0\),已知 \(a,b,c\),求解 \(x\)。
-
公式:\(\Delta=b^2-4ac\)
-
如果 \(\Delta < 0\),则无解。
-
如果 \(\Delta=0\),则有唯一解 \(x=\frac{-b}{2a}\)
-
如果 \(\Delta>0\),则有两个不同的解 \(x=\frac{-b±\sqrt{\Delta}}{2a}\)
-
推导
\[\begin{aligned}
&e*d = p*q - (p+q) + 2\\
&p + q = n-e*d+2 = m \\
&p*q = p * (m- p) = n, 结合上述方程,代入可得如下方程: \\ \\
&p^2 - m*p + n = 0 // 解此方程,求出 p \\
&\Delta = (-m)^2 - 4*1 *n = m^2 -4n \\
\\
&if(\Delta < 0) // NO 无解 \\
&else\{ \\
&\quad p = (m^2 ± \sqrt{\Delta})/2 \\
&\quad q = n/p \\
&\quad if(p > q) swap(p,q); \\
&\quad if(p*q==n \&\& p+q==m) // p q 就是答案 \\
&\quad else // NO 无解 \\
&\} \\
&\end{aligned}
\]
- 上述 \(O(1)\) 的说法其实不是那么准确,可以说是 \(O(\sqrt{n})\),主要在开方的时候,其复杂度一般是和牛顿迭代法相当的,比二分要优秀。
- sqrt() 复杂度介绍
- 方法3:二分答案 \(p\),单次复杂度 \(O(logn)\), 可以AC
- \(p*q=n, p+q=m\)
- 二分性质:两个正整数的和一定,那么差越小,乘积越大。
\[\begin{aligned}
&证明:令 a+b = n, a-b = m,\\
&则 a = \frac{n+m}{2}, b=\frac{n-m}{2},\\
&a*b = \frac{(n+m)*(n-m)}{4} = \frac{n^2-m^2}{4} \\
&由于 n是固定的,所以 m越小,a*b越大。
\end{aligned}
\]
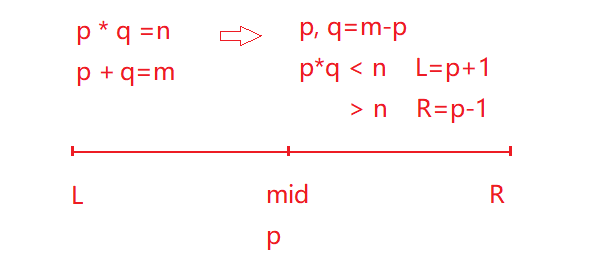
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10, INF = 0x3f3f3f3f, M = 1e9;
LL k, n, e, d;
int main() {
freopen("decode.in", "r", stdin);
freopen("decode.out", "w", stdout);
cin >> k;
for (int i = 1; i <= k; i++) {
cin >> n >> e >> d;
LL m = n + 2 - e * d;
LL delta = m * m - 4 * n;
if (delta < 0) cout << "NO" << endl;
else {
LL p = (m - (LL)sqrt(delta)) / 2;
LL q = (m + (LL)sqrt(delta)) / 2;
// LL l = 1, r = m - 1, p, q;
// while (l <= r) {
// p = l + r >> 1, q = m - p;
// if (p * q == n) break;
// else if (p * q < n) l = p + 1;
// else r = p - 1;
// }
// if (p > q) swap(p, q);
if (p * q == n && p + q == m)
cout << p << " " << q << endl;
else cout << "NO" << endl;
}
}
fclose(stdin), fclose(stdout);
return 0;
}
P8815 [CSP-J2022] 逻辑表达式
- 涉及知识点:大模拟,表达式树,栈
- 这和表达式求值的题目比较相似,只是计算对象变为三元组,确定优先级
- 另外就是计算的一些规则需要重新推导一下,如下图

点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e6+10,INF=0x3f3f3f3f, M=1e9;
unordered_map<char,int> pr {{'&', 2}, {'|', 1}};
/*
(v,a,b) = (value, and, or)
(1,a1,b1) & (v,a2,b2) = (v, a1+a2, b1+b2)
(0,a1,b1) | (v,a2,b2) = (v, a1+a2, b1+b2)
(0,a1,b1) & (v,a2,b2) = (0, a1+1, b1)
(1,a1,b1) | (v,a2,b2) = (1, a1, b1+1)
*/
struct T {
int v,a,b;
} pa,pb;
stack<T> num;
stack<char> op;
void cal() {
pb=num.top(), num.pop();
pa=num.top(), num.pop();
char c = op.top(); op.pop();
int a1=pa.a, b1=pa.b, v=pb.v, a2=pb.a, b2=pb.b;
if(c=='&') {
// (0,a1,b1) & (v,a2,b2) = (0,a1+1,b1)
// (1,a1,b1) & (v,a2,b2) = (v,a1+a2,b1+b2)
if(pa.v==0) num.push({0,a1+1,b1});
else num.push({v,a1+a2,b1+b2});
} else if(c=='|') {
// (0,a1,b1) | (v,a2,b2) = (v,a1+a2,b1+b2)
// (1,a1,b1) | (v,a2,b2) = (1,a1,b1+1)
if(pa.v==0) num.push({v,a1+a2,b1+b2});
else num.push({1,a1,b1+1});
}
}
int main() {
// freopen("data.in", "r", stdin);
string s;
while(cin>>s) {
// while(num.size()) num.pop();
// while(op.size()) op.pop();
for(int i=0; i<s.size(); i++) {
char c = s[i];
if(isdigit(c)) num.push({c-'0', 0, 0});
else if(c=='(') {
op.push(c);
} else if(c==')') {
while(op.top()!='(') cal();
op.pop();
} else {
while(op.size() && op.top()!=')' &&
pr[op.top()] >= pr[c]) cal();
op.push(c);
}
}
while(op.size()) cal();
cout<<num.top().v<<endl;
cout<<num.top().a<<" "<<num.top().b<<endl;
}
fclose(stdin); fclose(stdout); return 0;
}
P8816 [CSP-J2022] 上升点列
- 涉及知识点:最长上升子序列,二维DP
- 状态:\(f_{i,j}\) 表示 以第 \(i\) 个元素结尾,插入 \(j\) 个元素的最长上升序列长度。
- 转移:\(f_{i,j}=max\{f_{i,j-d}+d+1\} ,d = x2-x1+y2-y1-1\)
- 目标:\(ans=max\{f_{i,k}\}\)
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 510, M = 110, INF = 0x3f3f3f3f;
int n, k, f[N][M], ans = 0;
struct T {
int x, y;
bool operator<(const T& rhs) const {
if (x != rhs.x) return x < rhs.x;
return y < rhs.y;
}
} g[N];
// 状态:f[i][j] 表示序列以i结尾,添加j个点序列的最大长度
// 转移:f[i][j] = max(f[i][j], f[t][j-d]+d+1)
// d = x2-x1+y2-y1-1
int main() {
freopen("point.in", "r", stdin);
freopen("point.out", "w", stdout);
cin >> n >> k;
for (int i = 1, x, y; i <= n; i++) {
cin >> x >> y, g[i] = {x, y};
}
sort(g + 1, g + 1 + n);
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= k; j++) {
f[i][j] = j + 1;
for (int t = 1; t < i; t++) { // t -> i
if (g[t].x > g[i].x || g[t].y > g[i].y) continue;
int d = g[i].x - g[t].x + g[i].y - g[t].y - 1;
if (j >= d) f[i][j] = max(f[i][j], f[t][j - d] + d + 1);
}
ans = max(ans, f[i][j]);
}
}
cout << ans;
fclose(stdin), fclose(stdout);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号