P1823 [COI2007] Patrik 音乐会的等待

[COI2007] Patrik 音乐会的等待

题目描述

\(n\) 个人正在排队进入一个音乐会。人们等得很无聊，于是他们开始转来转去，想在队伍里寻找自己的熟人。

队列中任意两个人 \(a\) 和 \(b\)，如果他们是相邻或他们之间没有人比 \(a\) 或 \(b\) 高，那么他们是可以互相看得见的。

写一个程序计算出有多少对人可以互相看见。

输入格式

输入的第一行包含一个整数 \(n\)，表示队伍中共有 \(n\) 个人。

接下来的 \(n\) 行中，每行包含一个整数，表示人的高度，以毫微米(等于 \(10^{-9}\) 米)为单位，这些高度分别表示队伍中人的身高。

输出格式

输出仅有一行，包含一个数 \(s\)，表示队伍中共有 \(s\) 对人可以互相看见。

样例 #1

样例输入 #1

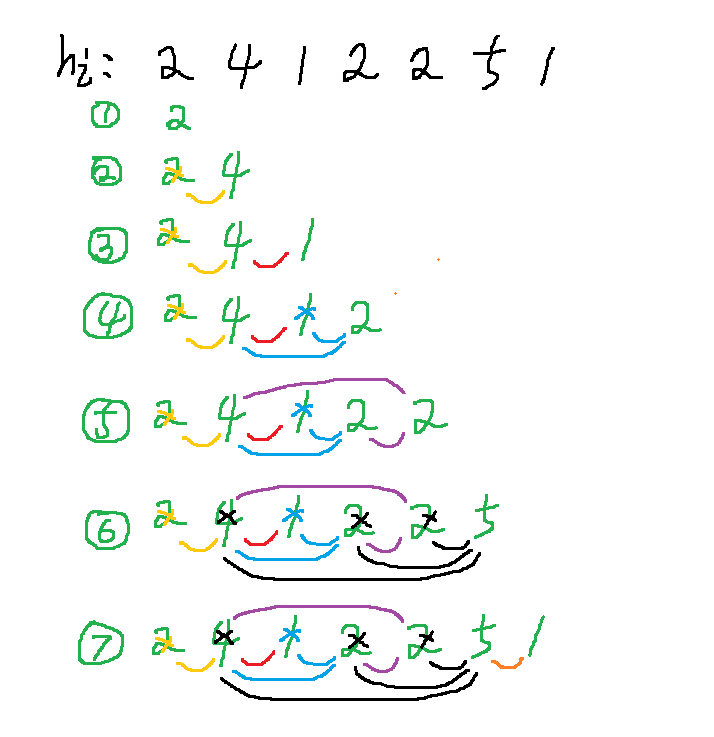
7 
2 
4 
1 
2 
2 
5 
1

样例输出 #1

10

提示

数据规模与约定

对于全部的测试点，保证 \(1\le\) 每个人的高度 \(< 2^{31}\)，\(1 \le n \le 5\times 10^5\)。

分析

• 法1：维护一个单调递增栈，但是需要查询相同元素，暴力查询复杂度 O(n^2)，二分优化到 O(nlogn)

• 法2：浪费的时间主要在查询相等元素个数的这一步，可以考虑将相同元素压缩成一个对象，用pair来封装（数值-数量），复杂度 O(n)。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e6+10,INF=0x3f3f3f3f;
int n,a[N],sta[N],head=0;
LL ans=0;

int bins(int x) {
    int l=1,r=head,p;
    while(l<r) {
        int mid=(l+r)>>1;
        if(a[sta[mid]] > x) l=mid+1;
        else r=mid;
    }
    if(a[sta[r]]==x) return head-r+1;
    else return 0;
}
void slove1() {
    for(int i=1; i<=n; i++) {
        while(head && a[sta[head]] < a[i]) {
            ans++, --head;
        }
        int l=head;
//        while(l && a[sta[l]]==a[i]) ans++, l--; // TLE
        int temp = bins(a[i]);
        ans+=temp, l-=temp;
        if(l && a[sta[l]] > a[i]) ans++;
        sta[++head] = i;
    }
}

pair<LL,LL> s[N];
void slove2() {
    for(int i=1; i<=n; i++) {
        pair<LL,LL> p(a[i],1);
        while(head && s[head].first <= a[i]) {
            ans += s[head].second;
            if(s[head].first==a[i]) p.second += s[head].second;
            head--;
        }
        if(head) ans++;
        s[++head] = p;
    }
}
int main() {
//    freopen("data.in", "r", stdin);
    scanf("%d",&n);
    for(int i=1; i<=n; i++) scanf("%d",&a[i]);
    slove1();
    printf("%lld\n",ans);
    return 0;
}