CSP2020 J2参考解析
P7071 [CSP-J2020] 优秀的拆分
- 涉及知识点:数组、模拟
- 解析:n<=1e7, 那么 2^30=1e9, 可以利用数组存储权值,在从大到小遍历,减去权值。
- 如果 n为奇数,那么肯定是没有答案的,直接输出 -1也有 20分。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int a[N], n, base=1, p=0;
int main(){
cin>>n;
while(base<=1e7) a[++p]=base, base<<=1;
if(n&1) cout<<-1;
else{
for(int i=p; i>=1; i--){
if(n>=a[i]) n-=a[i],cout<<a[i]<<" ";
}
}
return 0;
}
P7072 [CSP-J2020] 直播获奖
- 涉及知识点:模拟、排序
- 解析:可以直接模拟一遍,取分数线可以使用排序
- 如果使用 sort,整体复杂度 O(n^2log),预计得分 50.
- 可以使用插入排序优化,整体复杂度 O(n^2),预计得分 80.
如果排序后,计算分数,那么 \(i\) 选手的成绩评出之后,选择第 \(p\) 个人的分数划线,则该分数线为 \(a[i-p+1]\),如下图。
![image]()
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n,m,p,a[N];
int main(){
cin>>n>>m;
for(int i=1; i<=n; i++) cin>>a[i];
for(int i=1; i<=n; i++){
p = max(1, int(i*m/100));
for(int j=i; j>1; j--){
if(a[j]<a[j-1]) swap(a[j],a[j-1]);
else break;
}
cout<<a[i-p+1]<<" ";
}
return 0;
}
- 所以我们需要一个O(nlogn)的解法,主要在分数选择的地方确定一个O(log)级别的算法,可以考虑什么呢?
- 注意题目:每个选手的成绩均为不超过 600 的非负整数,所以分数线的区间是比较小的,那么就可以使用计数排序优化。
整体复杂度在 O(600*n),完美。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n,m,p,a[N],vis[N];
int main(){
cin>>n>>m;
for(int i=1; i<=n; i++) cin>>a[i];
for(int i=1; i<=n; i++){
p = max(1, int(i*m/100));
int cnt=0,score; vis[a[i]]++;
for(int j=600; cnt<p && j>=0; j--){
if(vis[j]) cnt+=vis[j],score=j;
}
cout<<score<<" ";
}
return 0;
}
P7073 [CSP-J2020] 表达式
-
涉及知识点:表达式、栈、表达式树
-
解析:后缀表达式
-
利用栈来模拟 ,单次询问复杂度O(s),整体复杂度 O(qs),预计 30分。
-
为了方便,我使用 map对变量进行映射,而 map的单次查询复杂度为 O(logn),所以增加了log的复杂度。
-
可以使用 unordered_map,建表耗时大,单次查询复杂度 O(1)。
-
考场上能写出 30分的代码已经很不错了,也要写一写。
-
那么如何得到满分解法呢?
-
我们发现 q<=1e5,时间主要是浪费在查询了,所以有没有办法可以 O(1) 查询呢?
-
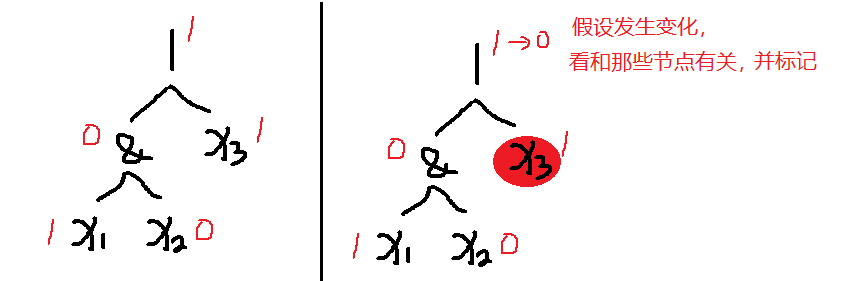
思考发现,数据只有 01,也就是变与不变,当修改一个数据后,结果不一定发生变化
-
后缀表达式,我们可以想到二叉树,可以根据表达式建立一棵表达式二次树
-
最后确定每个点的修改是否会影响结果,这样就可以保证 O(1) 查询了。
-
由于运算数的编号为 [1,n],那么运算符的编号可以从 n+1 开始。
-
这时候栈内存放的就不是运算数了,而是下标。
-
步骤1:建立表达式树,如下图
-
步骤2:dfs1遍历得到原始答案,dfs2遍历标记修改会对根节点有影响的节点。
![image]()
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n,m,a[N],b[N],sta[N],ps=0;
string s[N];
//map<string,int> mp;
unordered_map<string,int> mp;
///* 方法1:栈 + 模拟,score:30,TLE*/
void slove1() {
for(int i=1; i<=m; i++) {
stringstream ss; ss<<b[i];
string temp="x"; temp.append(ss.str());
mp[temp]=!mp[temp];
int top=0,ta=0,tb=0,tc=0;
for(int p=1; p<=ps; p++) {
if(s[p][0]=='x') {
sta[++top]=mp[s[p]];
} else if(s[p][0]=='!') {
ta=sta[top--];
sta[++top]=!ta;
} else {
ta=sta[top--], tb=sta[top--];
if(s[p][0]=='&') tc=ta&tb;
if(s[p][0]=='|') tc=ta|tb;
sta[++top]=tc;
}
}
cout<<sta[top]<<endl;
mp[temp]=!mp[temp]; // 还原
}
}
///* 方法2:建树,预处理 */
bool vis[N]; char c[N]; // c 操作符
struct T {
int lch,rch;
T(int a=0,int b=0):lch(a),rch(b) {}
} tree[N];
void add(int u,int v) {
if(!tree[u].lch) tree[u].lch=v;
else tree[u].rch=v;
}
int dfs1(int u) { // 得到原始答案
if(u<=n) return a[u];
if(c[u]=='!') return a[u]=!dfs1(tree[u].lch);
else if(c[u]=='&') {
int l=tree[u].lch,r=tree[u].rch,temp=1;
temp&=dfs1(l), temp&=dfs1(r);
return a[u]=temp;
} else if(c[u]=='|') {
int l=tree[u].lch,r=tree[u].rch,temp=0;
temp|=dfs1(l), temp|=dfs1(r);
return a[u]=temp;
}
}
void dfs2(int u) { // 预处理标记
vis[u]=1;
if(u<=n) return;
if(c[u]=='!') dfs2(tree[u].lch);
else {
int l=tree[u].lch,r=tree[u].rch;
if(c[u]=='&') {
if(a[l]==1) dfs2(r);
if(a[r]==1) dfs2(l);
} else if(c[u]=='|') {
if(a[l]==0) dfs2(r);
if(a[r]==0) dfs2(l);
}
}
}
void pr(int u) {
if(u==0) return;
cout<<"u="<<u<<" lch:"<<tree[u].lch<<" rch:"<<tree[u].rch
<<" a[u]:"<<a[u]<<" vis:"<<vis[u]<<endl;
pr(tree[u].lch);
pr(tree[u].rch);
}
void slove2() {
int top=0,ta=0,tb=0,tc=0,pc=n;
for(int p=1; p<=ps; p++) {
if(s[p][0]=='x') {
int temp=atoi(s[p].substr(1,s[p].size()-1).c_str());
sta[++top]=temp; // 栈内存放的是下标
} else if(s[p][0]=='!') {
ta=sta[top--], c[++pc]=s[p][0];
sta[++top]=pc, add(pc,ta);
} else {
ta=sta[top--], tb=sta[top--];
c[++pc]=s[p][0];
sta[++top]=pc, add(pc,ta),add(pc,tb);
}
}
int root=sta[top];
int ans=dfs1(root);
dfs2(root);
// pr(root);
// cout<<"root = "<<root<<" ans = "<<ans<<endl;
for(int i=1; i<=m; i++) {
if(vis[b[i]]) cout<<!ans<<endl;
else cout<<ans<<endl;
}
}
int main() {
// freopen("data.in", "r", stdin);
ios::sync_with_stdio(0);
while(1) {
cin>>s[++ps];
if(isdigit(s[ps][0])) break;
}
n = atoi(s[ps--].c_str());
for(int i=1; i<=n; i++) cin>>a[i];
cin>>m;
for(int i=1; i<=m; i++) cin>>b[i];
for(int i=1; i<=n; i++) {
stringstream ss; ss<<i;
string temp="x"; temp.append(ss.str());
mp[temp]=a[i];
}
// map<string,int>::iterator it=mp.begin();
// for(; it!=mp.end(); it++){
// cout<<it->first<<" "<<it->second<<endl;
// }
// slove1();
slove2();
return 0;
}
P7074 [CSP-J2020] 方格取数
-
涉及知识点:搜索、动态规划
-
解析:很多类似的题目,求方案数、最大\小和、最长\短路径等,都可以考虑 搜索,当然 TLE 是肯定的毕竟复杂度是 O(n!).
-
而本题相对于其他类似题目,主要在于多了一个可以向上走
-
那么可以想到,能否将其每一列看做一个阶段,求出该阶段下该点的最佳答案。
-
这样问题就变为两个常规的子问题:可以向上向右走、向下向右走,进行两次状态转移就行了。
-
需要注意:到 \((i,j)\) 的最大值一旦求出,则不能再上下转移,也就是只能向右转移了。
-
状态定义:\(f[i][j]\) 到达 \((i,j)\) 的最大值。
-
转态转移1:\(f[i][j]=max_{i=1}^{n}{f[i][j-1]}+a[i][j]\).
-
转态转移2:\(f[i][j]=max_{i=n}^{1}{f[i][j-1]}+a[i][j]\).
-
目标答案:\(f[n][m]\).
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e3+10,INF=0x3f3f3f3f;
int n,m,a[N][N],vis[N][N];
LL ans=-1e18,f[N][N];
int dis[][2]= {-1,0, 1,0, 0,1};
bool chk(int x,int y) {
if(x>=1&&x<=n&&y>=1&&y<=m&&!vis[x][y]) return 1;
return 0;
}
void dfs(int x,int y,LL sum) {
if(x==n&&y==m) {
ans=max(ans,sum); return ;
}
for(int i=0; i<3; i++) {
int tx=x+dis[i][0], ty=y+dis[i][1];
if(chk(tx,ty)) {
vis[tx][ty]=1;
dfs(tx,ty,sum+a[tx][ty]);
vis[tx][ty]=0;
}
}
}
void slove2(){
memset(f, -0x3f, sizeof(f));
f[1][0]=0;
for(int j=1; j<=m; j++){
LL s=-1e18;
for(int i=n; i>=1; i--){// 向上向右
s = max(s, f[i][j-1])+a[i][j];
f[i][j] = max(f[i][j], s);
}
s=-1e18;
for(int i=1; i<=n; i++){// 向下向右
s = max(s, f[i][j-1])+a[i][j];
f[i][j] = max(f[i][j], s);
}
}
cout<<f[n][m]<<endl;
}
int main() {
// freopen("data.in", "r", stdin);
cin>>n>>m;
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++) cin>>a[i][j];
// vis[1][1]=1, dfs(1,1,a[1][1]);
// cout<<ans<<endl;
slove2();
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号