CSP 2022 入门组第一轮
2022 CCF 非专业级别软件能力认证第一轮（CSP-J1）入门级 C++语言试题~解析hebin
认证时间：2022 年 9 月 18 日 09:30~11:30
考生注意事项：
- 试题纸共有 12 页，答题纸共有 1 页，满分 100 分。请在答题纸上作答，写在试题纸上的一律无效。
- 不得使用任何电子设备（如计算器、手机、电子词典等）或查阅任何书籍资料。
- 参考答案
一、单项选择题
（共 15 题，每题 2 分，共计 30 分；每题有且仅有一个正确选项）
-
以下哪种功能没有涉及 C++语言的面向对象特性支持：（ ）。
A. C++中调用 printf 函数
B. C++中调用用户定义的类成员函数
C. C++中构造一个 class 或 struct
D. C++中构造来源于同一基类的多个派生类
答案：A
这里提到了面向对象，那么我们需要知道什么事面向对象？(例：张三不想吃饭。)
面向对象（oritend-object，OO）：以问题根源作为关注点：人，饭
面向过程（oritend-process,OP）：以问题本身作为关注点：吃饭
printf是C语言中的一个输出函数，并不涉及到OOP特性，只要涉及到类(class)都是属于OOP特性。
面向对象编程中具有的三大特性：
封装：隐藏对象的属性和实现细节，仅对外提供公共访问方式。
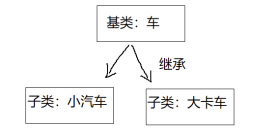
继承：将可复用的类作为基类（父类），子类继承父类，提高代码复用性。
多态：父类或接口定义的引用变量可以指向子类或具体实现类的实例对象。
这里老师给出一个概念画个图即可，如果没有学过后面的内容，讲多了会迷。
-
有 6 个元素，按照 6、5、4、3、2、1 的顺序进入栈 S，请问下列哪个出栈序列是非法的（ ）。
A. 5 4 3 6 1 2
B. 4 5 3 1 2 6
C. 3 4 6 5 2 1
D. 2 3 4 1 5 6
答案：C
栈：后进先出表（LIFO）
方法1：模拟，简单就不多说了，单选手必须掌握。
找规律：入栈降序序，出栈如果降序或者连续升序合法；当陡升时，元素应当为栈内最小值，四个选项中陡升情况如下。
A. 5 4 [3 6] 1 2；其中6是栈内最小值，合法。
B. 4 5 3 1 2 6
C. 3 [4 6] 5 2 1；其中6不是栈内最小值，应当为5。
D. 2 3 4 1 5 6 -
运行以下代码片段的行为是（ ）。
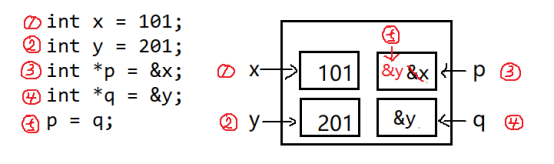
int x = 101;
int y = 201;
int *p = &x;
int *q = &y;
p = q;
A. 将 x 的值赋为 201
B. 将 y 的值赋为 101
C. 将 q 指向 x 的地址
D. 将 p 指向 y 的地址
答案：D
-
链表和数组的区别包括（ ）。
A. 数组不能排序，链表可以
B. 链表比数组能存储更多的信息
C. 数组大小固定，链表大小可动态调整
D. 以上均正确
答案：C
A. 错误；sort排序用的那么多，肯定错的，数组可以排序，链表可以排序；
理论上，任何数据结构都是可以规定其先后的，也就是排序。
B. 正确；链表比数组能存储更多的信息，我们说引入链表的原因就是因为数组的空间是连续的，而要开辟一段连续的很大的内存空间是不行的，于是可以开辟不连续的内存空间（节点），通过指针来连接各个空间，从而构建了链表。那么说链表比数组能存储更多的信息是正确的。
C. 正确；有人会说vector动态数组可以调整大小，C就错误了。但其实vector的本质是当数组a容量不够时，新建数组b并复制数组a的内容到b，之后销毁a，数组a，b本身的长度是固定的。
链表大小是通过节点数量确定的，而节点数量是可以变化的，所以链表大小可动态调整。
那么问题来说，答案不就选BC了吗？怎么多选了？
其实笔者认为题目稍微有点小问题，如果我是出题人，肯定会给BC都正确。
但是对于B.链表比数组能存储更多的信息，是具有一定的限制条件的，你可以试想一下，一个电脑内存设置空间大小刚好为可开长度为 N 的数组，并且内存已经开辟完了，那么如果使用链表，而链表是需要指针域来占用空间的，所以相比之下，数组的存储空间更大了。
所以建议加上限定条件：当内存一定时，.... -
对假设栈 S 和队列 Q 的初始状态为空。存在 e1~e6 六个互不相同的数据，每个数据按照进栈 S、出栈 S、进队列 Q、出队列 Q 的顺序操作，不同数据间的操作可能会交错。已知栈 S 中依次有数据 e1、e2、e3、e4、e5 和 e6 进栈，队列 Q 依次有数据 e2、e4、e3、e6、e5 和 e1 出队列。则栈 S 的容量至少是（ ）个数据。
A. 2 B. 3 C. 4 D. 6
答案：B
这个题目需要仔细读题，然后发现就是一个小模拟，没说的。
-
对表达式
a+(b-c)*d的前缀表达式为（ ），其中+、-、*是运算符。
A. *+a-bcd
B. +a*-bcd
C. abc-d*+
D. abc-+d
答案：B
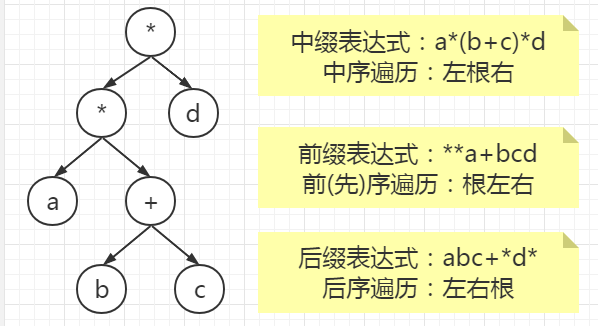
中缀表达式：a+b、前缀表达式：+ab、后缀表达式：ab+。
对于这个问题，我们可以将其中的某一部分看作一个整体，如 a+(b-c)*d 中(b-c)应当为一个数 x，所以对其变前缀就是 x=(-bc)。
原式就变为 a+x*d -> a+(*xd) -> +a(*xd) -> +a*-bcd。
这里可以结合二叉树的遍历方式一起回忆。
-
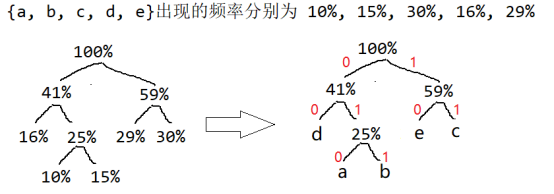
假设字母表 {a, b, c, d, e} 在字符串出现的频率分别为 10%, 15%, 30%, 16%, 29%。若使用哈夫曼编码方式对字母进行不定长的二进制编码，字母 d 的编码长度为（ ）位。
A. 1 B. 2 C. 2 或 3 D. 3
答案：B
哈夫曼编码基于信源的概率统计模型,它的基本思路是出现概率大的信源符号编短码，出现概率小的信源符号编长码，从而使平均码长最小。这是一种贪心策略，每次选取当前概率最大的符号使用现有的最短码。
构建：选择最小权值与次小权值组成一棵树，最小在左，并将其加入集合。
编码：规定哈夫曼树中的左分支为0，右分支为1，则从根结点到每个叶结点所经过的分支对应的 0和 1组成的序列便为该结点对应字符的编码。
-
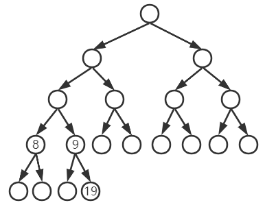
一棵有 n 个结点的完全二叉树用数组进行存储与表示，已知根结点存储在数组的第 1 个位置。若存储在数组第 9 个位置的结点存在兄弟结点和两个子结点，则它的兄弟结点和右子结点的位置分别是（ ）。
A. 8、18 B. 10、18 C. 8、19 D. 10、19
答案：C
-
考虑由 N 个顶点构成的有向连通图，采用邻接矩阵的数据结构表示时，该矩阵中至少存在（ ）个非零元素。
A. N-1 B. N C. N+1 D. N^2
答案：B
笔者认为描述不明确（权值无明确初始值，有向连通图表述不清楚）。
若从顶点 i 到顶点 j 有路径，则称顶点 i 和 j 是连通的。
若无向图 G 中任意两个顶点都连通，则称为连通图，否则称为非连通图。
若有向图 G 中任意两个顶点都连通，则称为强连通图。
有向图 G 中的极大强连通子图称为 G 的强连通分量。
思路：构造一个 N 个点的有向连通图，一个圆环 N 条边。
但是还没有加 a[i][i]=1 和特判 N=1 的情况，我认为这个题目有争议! -
以下对数据结构的表述不恰当的一项为：（ ）。
A. 图的深度优先遍历算法常使用的数据结构为栈。
B. 栈的访问原则为后进先出，队列的访问原则是先进先出。
C. 队列常常被用于广度优先搜索算法。
D. 栈与队列存在本质不同，无法用栈实现队列。
答案：D
深度优先遍历算法（dfs）是一条路到底，常用递归或栈完成；
广度优先搜索算法（bfs）是水波纹，多方向同时扩展，常使用队列完成；的访问原则为后进先出（LIFO），注意不要说FILO，这是不严谨的；
队列的访问原则是先进先出（FIFO）,这时候是可以说LILO。
栈与队列的本质是相同的，都是具有特殊限定的线性表，可以使用栈实现队列。
用staA-存放push数据，staB-临时翻转数据，这时候staB.top就是队首元素。 -
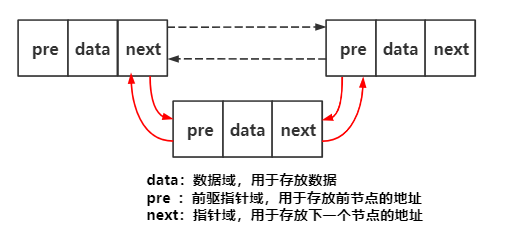
以下哪组操作能完成在双向循环链表结点 p 之后插入结点 s 的效果（其中，next 域为结点的直接后继，prev 域为结点的直接前驱）：（ ）。
A. p->next->prev=s; s->prev=p; p->next=s; s->next=p->next;
B. p->next->prev=s; p->next=s; s->prev=p; s->next=p->next;
C. s->prev=p; s->next=p->next; p->next=s; p->next->prev=s;
D. s->next=p->next; p->next->prev=s; s->prev=p; p->next=s;
答案：D
注意：本题目的答案可能不唯一，需要逐个带入验证。
-
以下排序算法的常见实现中，哪个选项的说法是错误的：（ ）。
A. 冒泡排序算法是稳定的
B. 简单选择排序是稳定的
C. 简单插入排序是稳定的
D. 归并排序算法是稳定的
答案：B
对于 a[i]=a[j]，且 i<j，排序后仍然满足 i<j，则称排序为稳定排序,否则为不稳定排序。
基数排序、冒泡排序、直接插入排序、归并排序是稳定的排序算法。
堆排序、快速排序、希尔排序、直接选择排序是不稳定的排序算法。 -
八进制数 32.1 对应的十进制数是（ ）。
A. 24.125
B. 24.250
C. 26.125
D. 26.250
答案：C
32.1(8)=(3*8+2).(1*1/8) = 26.125(2)。 -
一个字符串中任意个连续的字符组成的子序列称为该字符串的子串，则字符串 abcab 有（ ）个内容互不相同的子串。
A. 12
B. 13
C. 14
D. 15
解析：答案：B
可以其中每个字符作为起始字符，找出能组合的子串，最后去重。
a, ab, abc, abca, abcab
b, bc, bca, bcab
c, ca, cab
a, ab
b
空 -
以下对递归方法的描述中，正确的是：（ ）
A. 递归是允许使用多组参数调用函数的编程技术
B. 递归是通过调用自身来求解问题的编程技术
C. 递归是面向对象和数据而不是功能和逻辑的编程语言模型
D. 递归是将用某种高级语言转换为机器代码的编程技术
答案：B
递归的主要是通过调用自身来求解问题
A选项描述是没有问题的，但是不符合递归的主要思想。
C、D描述就直接错误了。
二、阅读程序
（程序输入不超过数组或字符串定义的范围；判断题正确填√，错误填×；除特殊说明外，判断题 1.5 分，选择题 3 分，共计 40 分）
(1)
#include <iostream>
using namespace std;
int main()
{
unsigned short x, y;
cin >> x >> y;
x = (x | x << 2) & 0x33;
x = (x | x << 1) & 0x55;
y = (y | y << 2) & 0x33;
y = (y | y << 1) & 0x55;
unsigned short z = x | y << 1;
cout << z << endl;
return 0;
}
假设输入的 x、y 均是不超过 15 的自然数，完成下面的判断题和单选题：
- 判断题
- 删去第 7 行与第 13 行的 unsigned，程序行为不变。（ ）
- 将第 7 行与第 13 行的 short 均改为 char，程序行为不变。（ ）
- 程序总是输出一个整数“0”。（ ）
- 当输入为“2 2”时，输出为“10”。（ ）
- 当输入为“2 2”时，输出为“59”。（ ）
- 单选题
- 当输入为“13 8”时，输出为（ ）。
A. “0” B. “209” C. “197” D. “226”
- 答案： √××× B
- 正确，删去unsigned后，变量位数为16bit，数据有符号，如果答案不变，那么在12行后需要保证x的最高位以及y的次高位为0，由于数据不超过15，是可以保证的。
- 错误，short 均改为 char，变量位数变为8bit，那么在12行后就不能保证x的最高位以及y的次高位为0。
- 错误，19. 错误 20. 错误，当输入为“2 2”时，输出为“12”。
- 带入计算即可，当输入为“13 8”时，输出为“209”。
（2）
#include <algorithm>
#include <iostream>
#include <limits>
using namespace std;
const int MAXN = 105;
const int MAXK = 105;
int h[MAXN][MAXK];
int f(int n, int m)
{
if (m == 1) return n;
if (n == 0) return 0;
int ret = numeric_limits<int>::max();
for (int i = 1; i <= n; i++)
ret = min(ret, max(f(n - i, m), f(i - 1, m - 1)) + 1);
return ret;
}
int g(int n, int m)
{
for (int i = 1; i <= n; i++)
h[i][1] = i;
for (int j = 1; j <= m; j++)
h[0][j] = 0;
for (int i = 1; i <= n; i++) {
for (int j = 2; j <= m; j++) {
h[i][j] = numeric_limits<int>::max();
for (int k = 1; k <= i; k++)
h[i][j] = min(
h[i][j],
max(h[i - k][j], h[k - 1][j - 1]) + 1);
}
}
return h[n][m];
}
int main()
{
int n, m;
cin >> n >> m;
cout << f(n, m) << endl << g(n, m) << endl;
return 0;
}
假设输入的 n、m 均是不超过 100 的正整数，完成下面的判断题和单选题：
- 判断题
- 当输入为“7 3”时，第 19 行用来取最小值的 min 函数执行了 449 次。（ ）
- 输出的两行整数总是相同的。（ ）
- 当 m 为 1 时，输出的第一行总为 n。（ ）
- 单选题
- 算法 g(n,m)最为准确的时间复杂度分析结果为（ ）。
A. \(𝑂(𝑛^{3/2}𝑚)\) B. \(𝑂(𝑛m)\) C. \(𝑂(𝑛^2𝑚)\) D. \(𝑂(𝑛𝑚^2)\) - 当输入为“20 2”时，输出的第一行为（ ）。
A. “4” B. “5” C. “6” D. “20” - （4 分）当输入为“100 100”时，输出的第一行为（ ）。
A. “6” B. “7” C. “8” D. “9”
答案： FTTCCB
22. 错误，当输入为“7 3”时，第 19 行用来取最小值的 min 函数执行了 448 次。
递归分析，打表：
定义 \(f[i][j]\) 表示输入 \((i,j)\) 时 min函数执行次数；
\(f[0][j]=0, f[i][1]=0;\)
\(f[i][j]=i+ \sum_{k=1}^{i} {(f[n-k][m]+f[k-1][m-1])};\)
如下方：黄色矩形元素和 ==> 32.
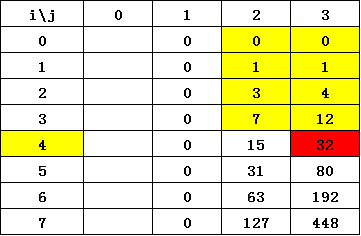
本题不建议通过 g函数来推导，如下：
for (int i = 1; i <= n; i++) {
for (int j = 2; j <= m; j++) { // m-2+1=2,可以确定答案一定是偶数
for (int k = 1; k <= i; k++){
min...
根据 g函数推导公式：\(f[n][m]=(m-2+1)*(1+n)*n/2\)
\(f[7][3]=56\)，这时候计算的其实就是 g函数中 min的执行次数了。
注意： g函数作为 f函数的递推形式，但是递推的本质就是记录子问题答案，防止重复求解，所以不能将 两个函数中min执行次数划等号。
-
输出的两行整数总是相同的。
正确，根据程序可以大概猜测，也可以自己根据递归函数写一下递推函数，看是否正确，或者模拟一遍. -
当 m 为 1 时，输出的第一行总为 n。
正确，第一行输出 f(n,m)，f(i,1)=n; -
算法 g(n,m)最为准确的时间复杂度分析结果为（ ）。
可以直接一眼看出来是 \(O(n^2*m)\)，也可以推导：
执行次数 \(f(n)=m*\sum_{i=1}^{n}i = m*(1+n)*n/2=>O(n^2*m)\) -
当输入为“20 2”时，输出的第一行为（ ）。
f(20,2)=min(ret, max(f(n - i, m), f(i - 1, m - 1)) + 1);
打表，带入数据计算。 -
（4 分）当输入为“100 100”时，输出的第一行为（ ）。
数据量较大，可以先猜一个，之后有时间再来验证。
备注：26，27 我没做，第一次做的时候计算错了，这两个题目可以放弃，计算量较大。
（3）
#include <iostream>
using namespace std;
int n, k;
int solve1()
{
int l = 0, r = n;
while (l <= r) {
int mid = (l + r) / 2;
if (mid * mid <= n) l = mid + 1;
else r = mid - 1;
}
return l - 1;
}
double solve2(double x)
{
if (x == 0) return x;
for (int i = 0; i < k; i++)
x = (x + n / x) / 2;
return x;
}
int main()
{
cin >> n >> k;
double ans = solve2(solve1());
cout << ans << ' ' << (ans * ans == n) << endl;
return 0;
}
假设 int 为 32 位有符号整数类型，输入的 n 是不超过 47000 的自然数、k 是不超过 int 表示范围的自然数，完成下面的判断题和单选题：
- 判断题
- 该算法最准确的时间复杂度分析结果为 𝑂(log 𝑛 + 𝑘)。（ ）
- 当输入为“9801 1”时，输出的第一个数为“99”。（ ）
- 对于任意输入的 n，随着所输入 k 的增大，输出的第二个数会变成“1”。（ ）
- 该程序有存在缺陷。当输入的 n 过大时，第 12 行的乘法有可能溢出，因此应当将 mid 强制转换为 64 位整数再计算。（ ）
- 单选题
- 当输入为“2 1”时，输出的第一个数最接近（ ）。
A. 1 B. 1.414 C. 1.5 D. 2 - 当输入为“3 10”时，输出的第一个数最接近（ ）。
A. 1.7 B. 1.732 C. 1.75 D. 2 - 当输入为“256 11”时，输出的第一个数（ ）。
A. 等于 16
B. 接近但小于 16
C. 接近但大于 16
D. 前三种情况都有可能
答案：TTFFCBA
28. 正确，slove1()的复杂度为 𝑂(log 𝑛），slove2()的复杂度为 O(𝑘)，需要注意：slove2(slove1())不是相乘，因为两者都是执行一次的。
29. 正确，当输入为“9801 1”时，输出的第一个数为“99”。
30. 错误，自然数包括 0,1,2,3..。
31. 错误，n=47000，mid=m/2, mid*mid=2.3e3x2.3e3=4e6，不会溢出。
32. 当输入为“2 1”时，输出的第一个数最接近 1.5。
上面的题目都是可以不用明白程序，直接推导出来答案的，之后的两个选项也可以但是比较麻烦，就需要了解程序的意义了！
- 牛顿迭代法求算术平方根
\(x*x=n\)，也可以记为 \(x=\sqrt{n}\)，其中\(\sqrt{n}\) 就被称为对 \(n\) 开根号。
\(x\) 就被称为 \(n\) 的算术平方根。
当给定 \(n\)，如何准确的求解 \(x\) 呢？
可以假定一个解 \(x_0\)，那么可以得到另外一个解：\(x_1=n/x_0\)，其中 \(x_0*x_1=n\)。
我们可以取两个解的平均值作为新解，再按照同样的方式继续推导满足误差的解。
于是得到迭代公式：\(x=(x+n/x)/2\);
#include<bits/stdc++.h>
using namespace std;
const double eps=1e-6;
double sqr(double n){
double x=n/2, temp=-1;
while(abs(x-temp) > eps)
temp = x, x = (x+n/x)/2;
return x;
}
int main(){
cout<<sqr(3)<<" "<<sqr(256)<<endl;
}
所以本题就是求解 sqrt(n);
sqrt(3) = 1.73205
sqrt(256) = 16
33. 当输入为“3 10”时，输出的第一个数最接近1.732。
34. 当输入为“256 11”时，输出的第一个数等于 16
三、完善程序
（单选题，每小题 3 分，共计 30 分）
（1）（枚举因数）从小到大打印正整数 n 的所有正因数。
试补全枚举程序。
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
vector<int> fac;
fac.reserve((int)ceil(sqrt(n)));
int i;
for (i = 1; i * i < n; ++i) {
if (①) {
fac.push_back(i);
}
}
for (int k = 0; k < fac.size(); ++k) {
cout << ② << " ";
}
if (③) {
cout << ④ << " ";
}
for (int k = fac.size() - 1; k >= 0; --k) {
cout << ⑤ << " ";
}
}
- ①处应填（ ）
A. n % i == 0 B. n % i == 1 C. n % (i-1) == 0 D. n % (i-1) == 1 - ②处应填（ ）
A. n / fac[k] B. fac[k] C. fac[k]-1 D. n / (fac[k]-1) - ③处应填（ ）
A. (i-1) * (i-1) == n B. (i-1) * i == n C. i * i == n D. i * (i-1) == n - ④处应填（ ）
A. n-i B. n-i+1 C. i-1 D. i - ⑤处应填（ ）
A. n / fac[k] B. fac[k] C. fac[k]-1 D. n / (fac[k]-1)
答案：ABCDA
35. 将因子放入vector，因子判断 （n%i==0）
36. 输出小于 sqrt(n) 的因子
37. 可能出现 i^2=n 的情况，需要输出一个 i
38. 因子是成对的，输出较大的一部分因子 (fac[k] --- n/fac[k])
（2）（洪水填充）现有用字符标记像素颜色的 8x8 图像。颜色填充的操作描述如下：给定起始像素的位置和待填充的颜色，将起始像素和所有可达的像素（可达的定义：经过一次或多次的向上、下、左、右四个方向移动所能到达且终点和路径上所有像素的颜色都与起始像素颜色相同），替换为给定的颜色。
试补全程序。
#include <bits/stdc++.h>
using namespace std;
const int ROWS = 8;
const int COLS = 8;
struct Point {
int r, c;
Point(int r, int c) : r(r), c(c) {}
};
bool is_valid(char image[ROWS][COLS], Point pt,
int prev_color, int new_color) {
int r = pt.r;
int c = pt.c;
return (0 <= r && r < ROWS && 0 <= c && c < COLS &&
① && image[r][c] != new_color);
}
void flood_fill(char image[ROWS][COLS], Point cur, int new_color) {
queue<Point> queue;
queue.push(cur);
int prev_color = image[cur.r][cur.c];
②;
while (!queue.empty()) {
Point pt = queue.front();
queue.pop();
Point points[4] = {③, Point(pt.r - 1, pt.c),
Point(pt.r, pt.c + 1), Point(pt.r, pt.c - 1)};
for (auto p : points) {
if (is_valid(image, p, prev_color, new_color)) {
④;
⑤;
}
}
}
}
int main() {
char image[ROWS][COLS] = {{'g', 'g', 'g', 'g', 'g', 'g', 'g', 'g'},
{'g', 'g', 'g', 'g', 'g', 'g', 'r', 'r'},
{'g', 'r', 'r', 'g', 'g', 'r', 'g', 'g'},
{'g', 'b', 'b', 'b', 'b', 'r', 'g', 'r'},
{'g', 'g', 'g', 'b', 'b', 'r', 'g', 'r'},
{'g', 'g', 'g', 'b', 'b', 'b', 'b', 'r'},
{'g', 'g', 'g', 'g', 'g', 'b', 'g', 'g'},
{'g', 'g', 'g', 'g', 'g', 'b', 'b', 'g'}};
Point cur(4, 4);
char new_color = 'y';
flood_fill(image, cur, new_color);
for (int r = 0; r < ROWS; r++) {
for (int c = 0; c < COLS; c++) {
cout << image[r][c] << " ";
}
cout << endl;
}
// 输出：
// g g g g g g g g
// g g g g g g r r
// g r r g g r g g
// g y y y y r g r
// g g g y y r g r
// g g g y y y y r
// g g g g g y g g
// g g g g g y y g
return 0;
}
- ①处应填（ ）
A. image[r][c] == prev_color
B. image[r][c] != prev_color
C. image[r][c] == new_color
D. image[r][c] != new_color - ②处应填（ ）
A. image[cur.r+1][cur.c] = new_color
B. image[cur.r][cur.c] = new_color
C. image[cur.r][cur.c+1] = new_color
D. image[cur.r][cur.c] = prev_color - ③处应填（ ）
A. Point(pt.r, pt.c)
B. Point(pt.r, pt.c+1)
C. Point(pt.r+1, pt.c)
D. Point(pt.r+1, pt.c+1) - ④处应填（ ）
A. prev_color = image[p.r][p.c]
B. new_color = image[p.r][p.c]
C. image[p.r][p.c] = prev_color
D. image[p.r][p.c] = new_color - ⑤处应填（ ）
A. queue.push(p)
B. queue.push(pt)
C. queue.push(cur)
D. queue.push(Point(ROWS,COLS))
答案：ABCDA
本题较为简单，考察BFS，这类题目建议做的时候先不看选项，自己写出合适的答案再对比选项。
40. check 位置的合法性，坐标越界，颜色等于上一个元素的颜色且没替换过。
41. 替换当前节点颜色
42. 四个方向，上下左右
43. 替换当前节点颜色
44. 元素入队
