图论合集

概念
邻接矩阵
- Floyed-Warshall - 弗洛伊德算法
邻接表：vector
- Dijkstra - 迪杰斯特拉算法
- Dijkstra - 堆优化
前向星
拓扑排序
强连通分量
- Tarjan 算法
并查集
最小生成树
- Prim - 普里姆算法
- Kruskal - 克鲁斯卡尔算法

本文主要是介绍图的建图、遍历、最短路以及一些图上算法，废话不多说，开整！

概念

图（Graph）由顶点集合（Vertex）和边集合（Edge）构成，记作：G=(V,E)。

无向图：如果代表边的顶点对是无序的，则称G为无向图，用圆括号序偶表示无向边，即 (vi,vj)。

有向图：如果表示边的顶点对是有序的，则称G为有向图，用尖括号序偶表示有向边，即 <vi,vj>。

邻接：若存在一条边 (i,j) 顶点i和顶点j为端点，它们互为邻接点。
若存在一条边 <i,j> 顶点i为起始端点（简称为起点），顶点j为终止端点（简称终点），它们互为邻接点，称vi邻接到vj， vj邻接于vi。
关联(依附)：边/弧与顶点之间的关系，如：存在 (vi, vj) / <vi, vj>，则称该边/弧关联于vi和vj。

顶点的度：与该顶点相关联的边的数目，记为 TD(v)。
无向图中，顶点的度等于该顶点相关联的边数。
有向图中, 顶点的度等于该顶点的入度与出度之和。
顶点 v 的入度是以 v 为终点的有向边的条数, 记作 ID(v)。
顶点 v 的出度是以 v 为始点的有向边的条数, 记作 OD(v)。

当有向图中仅1个顶点的入度为0,其余顶点的入度均为1，此时是何形状？
答案：一棵有向树

完全图：任意两个点都有一条边相连。
完全无向图：每两个顶点之间都存在着一条边，包含有 C(n,2) = n(n-1)/2条边。
完全有向图：每两个顶点之间都存在着方向相反的两条边，包含有 2C(n, 2) = n(n-1)条边。

稀疏图：一个图中含有较少的边数时（如 e<nlogn），称为稀疏图（Sparse graph）。

稠密图：当一个图接近完全图时，称为稠密图（Dense graph）。

也有这样的定义：有很少条边或弧（边的条数|E|远小于|V|²）的图称为稀疏图，反之边的条数|E|接近|V|²，称为稠密图。

权和网
图中每一条边都可以附带有一个对应的数值，这种与边相关的数值称为权(Weight)。
权可以表示从一个顶点到另一个顶点的距离或花费的代价。
边上带有权的图称为带权图，也称作网(Network)。

路径和路径长度
路径：在一个图G=(V，E)中，从顶点 i 到顶点 j 经过的所有点/边。
所有的(ix，iy)∈E(G)，或者<ix，iy>∈E(G)。
路径长度 是指一条路径上经过的边的数目。
若一条路径上除开始点和结束点可以相同外，其余顶点均不相同，则称此路径为 简单路径。

设有两个图G=(V, E)和G'=(V', E')，若V'是V的子集，E'是E的子集，则称G'是G的子图。

思考：设有一个图G=(V, E)，取V的子集V'，E的子集E'。那么 (V', E')一定是G的子图吗？

答案：如果点集不包含边集的所有顶点，子图就不成立。

回路或环
若一条路径上的开始点与结束点为同一个顶点，则此路径被称为回路或环。
开始点与结束点相同的简单路径被称为 简单回路或简单环。

连通、连通图和连通分量
无向图：若从顶点i到顶点j有路径，则称顶点i和j是 连通的。
若图中任意两个顶点都连通，则称为 连通图，否则称为 非连通图。

极大连通子图：该子图是G的连通子图，将G的任何不在该子图中的顶点加入，子图不再连通。

极小连通子图：该子图是G 的连通子图，在该子图中删除任何一条边，子图不再连通。

无向图G中的极大连通子图称为G的 连通分量。
显然，任何连通图的连通分量只有一个，即本身，而非连通图有多个连通分量。

强连通图和强连通分量
有向图：若从顶点i到顶点j有路径，则称从顶点i到j是连通的。
若图G中的任意两个顶点i和j都连通，即从顶点i到j和从顶点j到i都存在路径，则称图G是 强连通图。

有向图G中的极大强连通子图称为G的 强连通分量。
显然，强连通图只有一个强连通分量，即本身，非强连通图有多个强连通分量。

无向图：连通，连通图，连通分量，双连通分量
有向图：强连通，强连通图，强连通分量

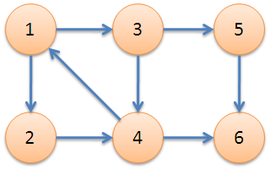
图中，子图 {1,2,3,4} 为一个强连通分量，因为顶点 1,2,3,4 两两可达。{5},{6} 也分别是两个强连通分量。

在图中找有向环。
扩展该有向环：如果某个顶点到该环中任一顶点有路径，并且该环中任一顶点到这个顶点也有路径，则加入这个顶点。
生成树：包含图中全部顶点的极小连通子图。
生成森林：对非连通图，由各个连通分量的生成树的集合。

欧拉路：从一个点S出发，不重不漏的经过每条边（允许重复经过一个点），最终去到另一个点T，的一条路径。

欧拉回路：从一个点S出发，不重不漏的经过每条边（允许重复经过一个点），最终回到这个点S，的一条路径。

欧拉图：存在欧拉回路的无向图。

欧拉路判定条件：一个无向图存在欧拉路当且仅当该图是连通的且有且只有2个点的度数是奇数，此时这两个点只能作为欧拉路径的起点和终点。

常用建图方式有

邻接矩阵
邻接表：vector
邻接表：链式前向星

各自有各自的优点，适合不同情况下的建图和图上算法

邻接矩阵

建立一个二维数组：G[N][N]，
G[i][j] = w 表示 i 点到 j点有一条路径权值为 w 的路。

常用于边数较多且不出现重边（两点间两条路）的情况，且由于空间限制点数不能过多（\(10^4\) 左右）。

#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10;
int n,m,G[N][N];
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1; i<=m; i++){
        int u,v,w; scanf("%d%d%d",&u,&v,&w);
        G[u][v] = G[v][u] = min(G[u][v], w);//无向图，权值为 w
    }
    for(int i=1; i<=n; i++){ // 输出查看存储方式
        for(int j=1; j<=n; j++) printf("%2d ",G[i][j]);
        printf("\n");
    }
    return 0;
}

Floyed-Warshall - 弗洛伊德算法

Floyed-Warshall 算法是多源最短路算法（求多个点到其余点的最短路），复杂度 \(O(n^3)\)。

通常用在点比较少的起点不固定的问题中，能解决负边（负权）但不能解决负环。

原理：当从 i 点到达 j 点，其实就只有两种走法，取其中最短路径的走法：

直接从 i 到 j；
从 i 到中间点 k，再从 k 到 j。

【参考程序】

#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10, INF=0x3f3f3f3f;
int n,m,G[N][N];// G[i][j]从 i到 j的最短路径

void floyed(){// 弗洛伊德算法
    for(int k=1; k<=n; k++) // 中间点，从 i到 j，中间只经过前 k个点
        for(int i=1; i<=n; i++)    // 起点
            for(int j=1; j<=n; j++)// 终点
                G[i][j]=min(G[i][j], G[i][k]+G[k][j]);
}
int main(){
    scanf("%d%d",&n,&m);
    memset(G, 0x3f, sizeof(G));
    for(int i=1; i<=n; i++) G[i][i]=0; //自环
    for(int i=1,u,v,w; i<=m; i++){
        scanf("%d%d%d",&u,&v,&w);
        G[u][v] = G[v][u] = min(G[u][v],w);
    }
    floyed();
    printf("%d\n", G[1][n]==INF ? -1 : G[1][n]);
    return 0;
}

总结：

利用动态规划解决任意两点间的最短路径的算法；
适合于有向图和无向图，稀疏图，可以解决带有负权边，判断是否存在负环的问题（判断负环：过程中，检测G[i][i]是否为负数即可）。
时间复杂度是 \(O(n^3)\)，时间复杂度比较高，不适合计算大数据；
不能解决带有“负权回路”（“负权环”）的图，因为带有“负权回路”的图没有最短路。

邻接表：vector

vector是一个动态数组，每当数组空间不足时，会重新分配空间，新空间为原空间的 2 倍。

由于分配空间、拷贝元素、撤销旧空间，使得vector的速度会较慢，但是平常使用是很不错的。

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10, INF=0x3f3f3f3f;
struct T{
    int v,w;
    T(){}
    T(int a,int b):v(a),w(b){}//构造函数
};
vector<T> G[N];
int n,m;
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1; i<=m; i++){
        int u,v,w; scanf("%d%d%d",&u,&v,&w);
        G[u].push_back(T(v,w)); //加边
        G[v].push_back(T(u,w));
    }
    for(int i=1; i<=n; i++){ // 输出查看存储方式
        printf("%d:", i);
        for(int j=0; j<G[i].size(); j++) printf("%d ", G[i][j]);
        printf("\n");
    }
    return 0;
}

Dijkstra - 迪杰斯特拉算法

Dijkstra 算法算是贪心思想实现的，其算法思想是：每次对到起始点最近且未访问过的点进行松弛操作，直到扩展到终点为止。

但是该算法不能用于求负权图，要求所有边的权重都为非负值。

对结点 v 进行松弛，就是判定是否 dis[v]>dis[u]+w[u,v]，如果该式成立则将 dis[v] 减小到 dis[u]+w[u,v]，否则不动。

松弛操作的原理是著名的定理：“三角形两边之和大于第三边”，通常叫它三角不等式。

【参考程序】

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10, INF=0x3f3f3f3f;
struct T{
    int v,w;
    T(){}
    T(int a,int b):v(a),w(b){}
};
vector<T> G[N];
int n,m,s,dis[N],vis[N];
void dijkstra(int s){//迪杰斯特拉-朴素算法
    memset(dis, 0x3f, sizeof(dis));
    memset(vis, 0x00, sizeof(vis));
    dis[s]=0;
    for(int i=1; i<=n; i++){
        int minv=INF, u=0;// u当前未处理前的最小路径所在节点
        for(int j=1; j<=n; j++){
            if(!vis[j] && dis[j]<minv) minv=dis[j], u=j;
        }
        if(u==0) break;
        vis[u]=1;
        for(int j=0; j<G[i].size(); j++){
            int v=G[i][j].v, w=G[i][j].w;
            if(dis[v]>dis[u]+w) dis[v]=dis[u]+w;
        }
    }
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1; i<=m; i++){
        int u,v,w; scanf("%d%d%d",&u,&v,&w);
        G[u].push_back(T(v,w)); //加边
        G[v].push_back(T(u,w));
    }
    dijkstra(1);
    printf("%d\n", dis[n]);
    return 0;
}

Dijkstra - 堆优化

优化：由于每次更新都是选择当前最小结点，那么可以使用小顶堆来存放结点。

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10, INF=0x3f3f3f3f;
struct T{
    int v,w;
    T(){}
    T(int a,int b):v(a),w(b){}
    bool operator< (const T& t) const{
        return w > t.w;
    }
};
vector<T> G[N];
int n,m,s,dis[N],vis[N];
void pri_dijkstra(int s){//迪杰斯特拉 - 堆优化
    memset(dis, 0x3f, sizeof(dis));
    memset(vis, 0x00, sizeof(vis));
    dis[s]=0;
    priority_queue<T> que; que.push(T(s,0));
    while(!que.empty()){
        T temp=que.top(); que.pop();
        int u=temp.v;
        if(vis[u]) continue;
        vis[u]=1;
        for(int i=0; i<G[u].size(); i++){
            T temp=G[u][i];
            int v=temp.v, w=temp.w;
            if(dis[v]>dis[u]+w){
                dis[v]=dis[u]+w;
                que.push(T(v,dis[v]));
            }
        }
    }
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1; i<=m; i++){
        int u,v,w; scanf("%d%d%d",&u,&v,&w);
        G[u].push_back(T(v,w)); //加边
        G[v].push_back(T(u,w));
    }
    pri_dijkstra(1);
    printf("%d\n", dis[n]);
    return 0;
}

总结：

Dijkstra 算法是单源最短路径算法，用于计算一个节点到其他所有节点的最短路径；
常用时间复杂度 O(n^2)，优化后可以达到 O(nlogn)，效率优于 Floyed；
适合于有向图和无向图，并且是解决权值均非负的最短路问题，不能解决负边问题；
稀疏图（点的范围很大但是边不多，边的条数|E|远小于|V|2）需要耗费比较多的空间。

前向星

前向星一种特殊的边集数组（存边的数组），先将边存储在数组中，将数组中的每条边按照起点从小到大排序，如果起点相同就按照终点从小到大排序，这样数组中起点相等的边就能够在数组中进行连续访问，并记录下以某个点为起点的所有边在数组中的起始位置和存储长度，前向星就构造好了。

用 len[i] 来记录所有以i为起点的边在数组中的存储长度。

用 head[i] 记录以i为边集在数组中的第一个存储位置。

利用前向星可以在 O(1)的时间找到以 i 为起点的第一条边，以 O(len[i]) 的时间找到以 i 为起点的所有边。

优点是实现简单，容易理解。

缺点是需要排序，带来了时间开销，实用性也较差，只适合离线算法，如果用链式前向星，就可以避免排序。

输入数据

第 1 行，2 个整数 N,M。

接下来 M 行，每行 2 个整数 Ui,Vi，表示边 (Ui,Vi)。点用 1,2,?,N 编号。

输出数据

序号：0 1 2 3 4 5 6
起点：1 1 1 2 3 4 4
终点：2 3 5 3 4 1 5
head：0 1 4 5 6
len ：0 3 1 1 2

程序实现

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10, INF=0x3f3f3f3f;
int head[N],len[N],cnt,n,m;
struct T{
    int u,v;
    bool operator< (const T& t){
        if(u!=t.u) return u < t.u;
        return v < t.v;
    }
}G[N];  // 边集数组
void add(int u,int v){
    G[cnt].u = u, G[cnt].v = v;
    cnt++;
}
void pr(){
    printf("\n序号："); for(int i=0; i<m; i++) printf("%d ", i);
    printf("\n起点："); for(int i=0; i<m; i++) printf("%d ", G[i].u);
    printf("\n终点："); for(int i=0; i<m; i++) printf("%d ", G[i].v);
    printf("\nhead："); for(int i=0; i<n; i++) printf("%d ", head[i]);
    printf("\nlen : "); for(int i=0; i<n; i++) printf("%d ", len[i]);
}
int main(){
    freopen("data.in", "r", stdin);
    scanf("%d%d", &n, &m);
    for(int i=1; i<=m; i++){
        int u,v; scanf("%d%d", &u,&v); add(u, v);
    }
    sort(G, G+m);
    for(int i=0; i<m; i++){
        if(head[G[i].u]==0) head[G[i].u]=i+1;
        len[G[i].u]++;
    }
    pr();
    return 0;
}

基于边集数组的 bellman-ford 算法

Bellman-ford 算法适用于单源最短路径，图中边的权重可为负数即负权边，但不可以出现负权环。

算法原理：

有 n 个点的图中起始点的最短路径最多只有 n-1 条边。
对所有边循环 n-1 次更新：dis[v]=min(dis[v], dis[u]+w(u,v));

算法步骤：

初始化所有 dis[s]，源点 dis[s]=0，其他 dis[s]=INF；
进行 n-1 次循环，在循环体中遍历所有的边，进行松弛计算：dis[v]=min(dis[v], dis[u]+w(u,v));
遍历图中所有的边，检验是否可以继续松弛，若可以则证明存在负权环，没有最短路。

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10, INF=0x3f3f3f3f;
int n,m,s,dis[N],pre[N];// pre[i]表示 i的前驱
struct T {
    int u,v,w;
    T() {}
    T(int a,int b,int c):u(a),v(b),w(c) {}
} G[N];
bool bellman_ford() {
    memset(dis, 0x3f, sizeof(dis));
    dis[s]=0;
    for(int i=1; i<n; i++) {  // 执行 n-1 次
        for(int j=1; j<=m; j++) {
            int u=G[j].u, v=G[j].v, w=G[j].w;
            if(dis[v] > dis[u]+w) {
                dis[v]=dis[u]+w;
                pre[v] = u;
            }
        }
    }
    for(int i=1; i<=m; i++) { // 负权环判断，还可以进行松弛操作，则存在负权环
        if(dis[G[i].v] > dis[G[i].u]+G[i].w) return 0;
    }
    return 1;
}
void pr(int root) { // 打印最短路的路径
    if(root==pre[root]) {
        printf("%d",root); return;
    }
    pr(pre[root]);
    printf("->%d",root);
}
int main() {
    freopen("data.in", "r", stdin);
    scanf("%d%d%d",&n,&m,&s);
    pre[s]=s;
    for(int i=1; i<=m; i++) {
        int u,v,w; scanf("%d%d%d",&u,&v,&w);
        G[i]=T(u,v,w);
    }
    bool flag = bellman_ford();
    if(flag==0) printf("NO\n");
    else {
        for(int i=1; i<=n; i++) {
            printf("i=%2d, dis:%2d, path:",i,dis[i]);
            pr(i);
            printf("\n");
        }
    }
    return 0;
}

链式前向星

链式前向星其实就是用数组模拟链表，和邻接表类似，也是链式结构和线性结构的结合，每个结点 i 都有一个链表，链表的所有数据是从 i 出发的所有边的集合（对比邻接表存的是顶点集合）。

时间效率为O(m)，空间效率为O(m)，遍历效率为O(m)

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10, INF=0x3f3f3f3f;
int n,m,s,dis[N],vis[N],head[N],cnt=0;
struct T{
    int to,w,next;
}G[N<<1];
void add(int u,int v,int w){
    G[++cnt].to = v;      // 第cnt条边指向那个点
    G[cnt].w = w;         // 第cnt条边的权值
    G[cnt].next = head[u];// 第cnt条边的下一条边的序号
    head[u] = cnt;        // 以u点为初始结点的边的序号
}
int main(){
    memset(head, 0xff, sizeof(head));
    scanf("%d%d",&n,&m);
    for(int i=1; i<=m; i++){
        int u,v,w; scanf("%d%d%d",&u,&v,&w);
        add(u,v,w), add(v,u,w);
    }
    for(int i=1; i<=n; i++){// 输出查看存储方式
        printf("%d:", i);   // 链式前向星的遍历方式如下
        for(int j=head[i]; ~j; j=G[j].next)
            printf("<%2d,%2d> ",G[j].to,G[j].w);
        printf("\n");
    }
    return 0;
}

基于链式前向星的 dijkstra 及其堆优化

优化：每次选择最小结点的时候，可以使用小顶堆来完成。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+10, INF=0x3f3f3f3f;
int head[N],cnt=0,dis[N],vis[N],n,m;
struct T {
    int to,w,next;
    T() {}
    T(int a,int b):to(a),w(b) {}
    bool operator< (const T& t) const {
        return w > t.w;
    }
} G[N];
void add(int u,int v,int w) {
    G[++cnt].to = v;
    G[cnt].w = w;
    G[cnt].next = head[u];
    head[u] = cnt;
}
void dijkstra(int s) { // 迪杰斯特拉-朴素算法
//    fill(dis, dis+N, INF);  // 执行速度慢，对于某些题目会被卡时 
//    fill(vis, vis+N, 0);
    memset(dis, 0x3f, sizeof(dis));
    memset(vis, 0x00, sizeof(vis));
    dis[s] = 0;
    for(int i=1; i<=n; i++) {
        int u=0, minv=INF;// u 当前集合最小值
        for(int j=1; j<=n; j++) {
            if(!vis[j] && dis[j]<minv) u=j, minv=dis[j];
        }
        if(u==0) break;
        vis[u]=1;
        for(int j=head[u]; ~j; j=G[j].next) {
            int v=G[j].to, w=G[j].w;
            if(dis[v] > dis[u]+w) dis[v] = dis[u]+w;
        }
    }
}
void pri_dijkstra(int s) {// 迪杰斯特拉-堆优化
    memset(dis, 0x3f, sizeof(dis));
    memset(vis, 0x00, sizeof(vis));
    dis[s] = 0;
    priority_queue<T> que; que.push(T(s,dis[s]));
    while(!que.empty()) {
        int u=que.top().to;  que.pop();
        if(vis[u]) continue;
        vis[u]=1;
        for(int i=head[u]; ~i; i=G[i].next) {
            int v=G[i].to, w=G[i].w;
            if(dis[v] > dis[u]+w) {
                dis[v] = dis[u]+w;
                que.push(T(v,dis[v]));
            }
        }
    }
}
int main() {
    fill(head, head+N, -1);
    scanf("%d%d", &n,&m); int u,v,w;
    for(int i=1; i<=m; i++) {
        scanf("%d%d%d", &u,&v,&w);
        add(u,v,w), add(v,u,w);
    }
//    dijkstra(1);
    pri_dijkstra(1);
    printf("%d\n", dis[n]==INF? -1 : dis[n]);
    return 0;
}

基于链式前向星的 spfa 算法

Bellman-ford 算法中松弛操作一定是发生在最短路径松弛过的前驱结点上，所以可以使用队列记录松弛过的结点，这就是SPFA算法。

SPFA算法（动态逼近法）步骤

读取队头顶点 u，并将队头顶点 u 出队并消除标记；
将与点 u 相连的所有点 v 进行松弛操作，如果能更新估计值（即令dis[v]变小），那么就更新；
如果点 v 没有在队列中，那么要将点 v 入队并标记，如果已经在队列中了，那么就不用入队；
以此循环，直到队空为止就完成了单源最短路的求解。

SPFA的运用和分析运用：

求单源最短路（可以有负权）；
判断负环(某个点进队的次数超过了v次，则存在负环)
平均时间复杂度：O(kE)，k是一个常数。
最差时间复杂度：O(VE) (可能设计卡spfa时间复杂度的数据)

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10, INF=0x3f3f3f3f;
int head[N],dis[N],vis[N],cnt,n,m,num[N];
struct T{
    int to,w,next;
    T(){}
    T(int a,int b):w(a),to(b){}
    bool operator< (const T& t) const{
        return w > t.w;
    }
}G[N];
void add(int u,int v,int w){
    G[++cnt].to = v;
    G[cnt].w = w;
    G[cnt].next = head[u];
    head[u] = cnt;
}
bool spfa(int s){
    memset(dis, 0x3f, sizeof(dis));
    dis[s]=0;
    queue<int> que; que.push(s);
    vis[s] = 1;
    while(!que.empty()){
        int u=que.front(); que.pop();
        vis[u] = 0;
        for(int i=head[u]; ~i; i=G[i].next){
            int v=G[i].to, w=G[i].w;
            if(dis[v] > dis[u]+w){
                dis[v] = dis[u]+w;
                num[v] = num[u]+1;
                if(num[v]>=n) return 0; //存在负环
                if(!vis[v]){
                    que.push(v);
                    vis[v] = 1;
                }
            }
        }
    }
    return 1; //不存在负环
}
int main(){
    scanf("%d%d", &n,&m);
    memset(head, -1, sizeof head);
    for(int i=1; i<=m; i++){
        int u,v,w; scanf("%d%d%d", &u,&v,&w);
        add(u,v,w), add(v,u,w);
    }
    bool flag = spfa(1);
    if(flag==0) printf("NO\n");
    else printf("%d ", dis[n]);
    return 0;
}

请使用上述多种算法解决下面的题目

拓扑排序

对一个有向无环图(Directed Acyclic Graph简称DAG) G 进行拓扑排序，
是将 G 中所有顶点排成一个线性序列，使得图中任意一对顶点 u 和 v，若边 <u,v>∈E(G)，则 u 在线性序列中出现在 v 之前。

通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。
简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

由 AOV 网构造拓扑序列的拓扑排序算法主要是循环执行以下两步，直到不存在入度为0的顶点为止。

选择一个入度为0的顶点并输出之;
从网中删除此顶点及所有出边，再循环上述步骤。
循环结束后，若输出的顶点数小于网中的顶点数，则输出"有回路"信息，否则输出的顶点序列就是一种拓扑序列。

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10, INF=0x3f3f3f3f;
int n,m,s,dis[N],vis[N],head[N],cnt=0,ru[N];
struct T{
    int to,w,next;
}G[N<<1];
queue<int> que;
vector<int> ve;
void add(int u,int v,int w){
    G[++cnt].to = v;
    G[cnt].w = w;
    G[cnt].next = head[u];
    head[u] = cnt;
}
void topSort(){ // 拓扑排序
    for(int i=1; i<=n; i++){
        if(ru[i]==0){
            que.push(i);
            ve.push_back(i);
        }
    }
    while(!que.empty()){
        int u = que.front(); que.pop();
        for(int i=head[u]; ~i; i=G[i].next){
            int v = G[i].to;
            ru[v]--;
            if(ru[v]==0){
                que.push(v);
                ve.push_back(v);
            }
        }
    }
}
int main(){
    memset(head, 0xff, sizeof(head));
    scanf("%d%d",&n,&m);
    for(int i=1; i<=m; i++){
        int u,v,w; scanf("%d%d%d",&u,&v,&w);
        add(u,v,w); ru[v]++;
    }
    topSort();
    if(ve.size()!=n) printf("有环\n");
    else{
        for(int i=0; i<ve.size(); i++){
            printf("%d ", ve[i]);
        }
    }
    return 0;
}

强连通分量

无向图：连通，连通图，连通分量，双连通分量
有向图：强连通，强连通图，强连通分量

如果两个顶点可以相互通达，则称两个顶点强连通。
如果有向图G的每两个顶点都强连通，称G是一个强连通图。
有向图的极大强连通子图，称为强连通分量。

图中，子图 {1,2,3,4} 为一个强连通分量，因为顶点 1,2,3,4 两两可达。{5},{6} 也分别是两个强连通分量。

Tarjan算法是用来求有向图的强连通分量的。

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。

搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

定义DFN(u)为节点u搜索的次序编号(时间戳)，Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。

当DFN(u)=Low(u)时，以u为根的搜索子树上所有节点是一个强连通分量。

接下来是对算法流程的演示。

从节点1开始DFS，把遍历到的节点加入栈中。搜索到节点u=6时，DFN[6]=LOW[6]，找到了一个强连通分量。退栈到u=v为止，{6}为一个强连通分量。
返回节点5，发现DFN[5]=LOW[5]，退栈后{5}为一个强连通分量。
返回节点3，继续搜索到节点4，把4加入堆栈。发现节点4向节点1有后向边，节点1还在栈中，所以LOW[4]=1。节点6已经出栈，(4,6)是横叉边，返回3，(3,4)为树枝边，所以LOW[3]=LOW[4]=1。
继续回到节点1，最后访问节点2。访问边(2,4)，4还在栈中，所以LOW[2]=DFN[4]=5。返回1后，发现DFN[1]=LOW[1]，把栈中节点全部取出，组成一个连通分量{1,3,4,2}。
至此，算法结束。经过该算法，求出了图2中全部的三个强连通分量{1,3,4,2},{5},{6}。

可以发现，运行Tarjan算法的过程中，每个顶点都被访问了一次，且只进出了一次堆栈，每条边也只被访问了一次，所以该算法的时间复杂度为O(N+M)。

Tarjan 算法

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
struct T{
    int v,w,next;
}G[N];
int n,m,head[N],cnt,dfn[N],low[N],vis[N];
int depth, sta[N],top, sum;
void add(int u,int v,int w){
    G[++cnt].v = v;
    G[cnt].w = w;
    G[cnt].next = head[u];
    head[u] = cnt;
}
void tarjan(int u){
    dfn[u] = low[u] = ++depth;
    vis[u] = 1;
    sta[++top] = u;
    for(int i=head[u]; ~i; i=G[i].next) {
        if(!dfn[G[i].v]) {       // 未访问过
            tarjan(G[i].v);
            low[u] = min(low[u], low[G[i].v]);
        } else if(vis[G[i].v]) { // 还在栈内
            low[u] = min(low[u], dfn[G[i].v]);
        }
    }
    if(low[u]==dfn[u]) {         // 构成强连通分量
        do{
            printf("%d ", sta[top]);
            vis[sta[top]] = 0;
        } while(u != sta[top--]);
        puts("");
    }
}
int main(){
    memset(head, -1, sizeof(head));
    scanf("%d%d",&n,&m);
    for(int i=1; i<=m; i++) {
        int u,v,w=1; scanf("%d%d",&u,&v);
        add(u,v,w);
    }
    for(int i=1; i<=n; i++){
        if(!dfn[i]) tarjan(i);  // 防止图没走完
    }
    return 0;
}

下列内容目前选修：

缩点就是把分量中的点和边用一个点来表示。
强连通分量缩点之后就是一个有向无环图。

割点：无向连通图中，去掉一个顶点和它相邻的所有边，图中连通分量增加，则该顶点称为割点。
桥（割边）：无向连通图中，去掉一条边，图中的连通分量数增加，则该边称为桥或割边。

双连通分量又分点双连通分量和边双连通分量两种。
若一个无向图中的去掉任意一个节点(一条边)都不会改变此图的连通性，即不存在割点(桥)，则称作点(边)双连通图。
一个无向图中的每一个极大点(边)双连通子图称作此无向图的点(边)双连通分量。求双连通分量可用Tarjan算法。

https://baike.so.com/doc/9441199-9782210.html

欧拉回路...

POJ 1236 Network of Schools
POJ 3177 Redundant Paths

并查集

并查集是一种用于管理元素所属集合的数据结构，实现为一个森林，其中每棵树表示一个集合，树中的节点表示对应集合中的元素。

顾名思义，并查集支持两种操作：

合并（Union）：合并两个元素所属集合（合并对应的树）
查询（Find）：查询某个元素所属集合（查询对应的树的根节点），这可以用于判断两个元素是否属于同一集合

并查集在经过修改后可以支持单个元素的删除、移动；使用动态开点线段树还可以实现可持久化并查集。

int p[N];
void init(int n){ // 初始化， p[i]=i 自己是自己的父亲
    for(int i=0; i<=n; i++) p[i]=i;
}
int find(int u){ // 查询 u 的父亲
    return u==p[u] ? u:p[u]=find(p[u]);
}
void merge(int u,int v){ // 合并 u，v，使得其为同一个家族
    int a=find(u), b=find(v);
    p[a] = b;
}

最小生成树

对于带权连通图 G （每条边上的权均为大于零的实数），可能有多棵不同生成树。

每棵生成树的所有边的权值之和可能不同，其中权值之和最小的生成树称为图的最小生成树。

找到连通图的最小生成树，有两种经典的算法：普里姆(Prim)算法和克鲁斯卡尔(Kruskal)算法。

POJ 1258

Prim - 普里姆算法

算法步骤

从图中某一个顶点出发；
选择一个顶点在生成树中，而另一个顶点不在生成树的连接权值最小的顶点进行连接；
重复上一步，直到所有结点都连接上。

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
const int INF=0x3f3f3f3f;
const int N=1e3+10;
int G[N][N],n,m,closest[N],lowcost[N],vis[N];

int prim(int u) {
    memset(vis, 0x00, sizeof(vis));
    vis[u] = 1;
    lowcost[u] = 0;
    for(int i=1; i<=n; i++) {
        closest[i] = u, lowcost[i] = G[u][i];
    }
    for(int i=1; i<n; i++) { // 将剩余 n-1个点加入集合
        int temp=INF, k=u;   // k 为在非生成树中寻找的最小节点
        for(int j=1; j<=n; j++) {
            if(!vis[j] && lowcost[j]<temp) {
                temp = lowcost[j], k=j;
            }
        }
        if(k==u) return -1; // 非联通图，不存在最小生成树
        vis[k] = 1;         // 标记加入生成树
        for(int j=1; j<=n; j++) {
            if(!vis[j] && G[k][j]<lowcost[j]) {
                closest[j] = k, lowcost[j] = G[k][j];
            }
        }
    }
    int ans=0; //最小生成树的权值
    for(int i=1; i<=n; i++) ans += lowcost[i];
    return ans;
}
int main() {
    freopen("data.in", "r",stdin);
    while(~scanf("%d",&n)) {
        for(int i=1; i<=n; i++) {
            for(int j=1; j<=n; j++) scanf("%d", &G[i][j]);
        }
        printf("%d\n", prim(1));
    }
    return 0;
}

Kruskal - 克鲁斯卡尔算法