02. 数组综合
02. 数组综合
一维数组排序
【题目描述】给定 N(N<1e4)个不大于 1000的整数,输出它的非降序列。
【输入样例】
6
3 2 4 1 5 3
【输出样例】
1 2 3 3 4 5
【参考程序】
#include<iostream>
#include<algorithm> //sort
using namespace std;
const int N=1e4+10;
int a[N];
int main(){
int n; cin>>n;
for(int i=0; i<n; i++) {
cin>>a[i];
}
sort(a, a+n);//内部封装快速排序,默认升序排序
for(int i=0; i<n; i++) {
cout<<a[i]<<" ";
} cout<<endl;
return 0;
}
字符数组
【题目描述】给定一个长度小于 1e4的字符串,按照 ASCII码输出它的非降序列。
【输入样例】acdb
【输出样例】abcd
【参考程序】
#include<iostream>
#include<algorithm> //sort
#include<cstring> //strlen
using namespace std;
const int N=1e4+10;
char a[N];
int main(){
scanf("%s", a); //给字符数组赋值,不需要加 &
int n=strlen(a); //求字符数组中元素个数, 以 '\0' 作为结束符
sort(a, a+n); //内部封装快速排序,默认升序排序
printf("%s\n", a);//字符数组直接输出,for循环输出也可以
return 0;
}
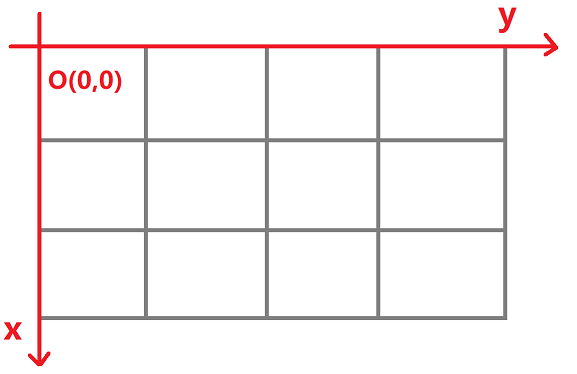
二维数组画地图,构建平面直角坐标系
B2099 矩阵交换行
【题目描述】
给定一个 5×5 的矩阵(数学上,一个 r×c 的矩阵是一个由 r 行 c 列元素排列成的矩形阵列),
将第 n 行和第 m 行交换,输出交换后的结果。
【输入格式】
输入共 6 行,前 5 行为矩阵的每一行元素,元素与元素之间以一个空格分开。
第 6 行包含两个整数 m、n,以一个空格分开(1≤m,n≤5)。
【输出格式】
输出交换之后的矩阵,矩阵的每一行元素占一行,元素之间以一个空格分开。
【输入样例】
1 2 2 1 2
5 6 7 8 3
9 3 0 5 3
7 2 1 4 6
3 0 8 2 4
1 5
【输出样例】
3 0 8 2 4
5 6 7 8 3
9 3 0 5 3
7 2 1 4 6
1 2 2 1 2
【参考程序】
#include<iostream>
#include<algorithm> //sort
#include<cstring> //strlen
using namespace std;
const int N=10;
int a[N][N], r=5; //矩阵稍微多开一点
int main() {
for(int i=1; i<=r; i++) {
for(int j=1; j<=r; j++) {
cin>>a[i][j];
}
}
int m,n; cin>>m>>n;
for(int j=1; j<=r; j++) {
int temp = a[m][j];//三桶水的交换
a[m][j] = a[n][j];
a[n][j] = temp;
}
//swap(a[m], a[n]); //也可以直接交换一行
for(int i=1; i<=r; i++) {
for(int j=1; j<=r; j++) {
cout<<a[i][j]<<" ";
}
cout<<endl;
}
return 0;
}
B2101 计算矩阵边缘元素之和
【题目描述】
输入一个整数矩阵,计算位于矩阵边缘的元素之和。
所谓矩阵边缘的元素,就是第一行和最后一行的元素以及第一列和最后一列的元素。
【输入格式】
第 1 行包含两个整数,分别为行数 m 和列数 n,两个整数之间空格隔开。
第 2 行开始有 m 行数据,每行包含 n 个整数,整数之间空格隔开。
【输出格式】
对应矩阵的边缘元素和。
【输入样例】
3 3
3 4 1
3 7 1
2 0 1
【输出样例】
15
【数据范围】1≤m,n≤100。
【参考程序】
#include<iostream>
using namespace std;
const int N=110;
int a[N][N], sum=0;
int main() {
int n,m; cin>>n>>m;
for(int i=1; i<=n; i++) {
for(int j=1; j<=m; j++) {
cin>>a[i][j];
}
}
for(int i=1; i<=n; i++) {
for(int j=1; j<=m; j++) {
if(i==1) sum+=a[i][j]; //第一行
else if(i==n) sum+=a[i][j]; //最后一行
else if(j==1) sum+=a[i][j]; //第一列
else if(j==m) sum+=a[i][j]; //最后一列
}
}
cout<<sum<<endl;
return 0;
}
B2104 矩阵加法
【题目描述】
输入两个 n 行 m 列的矩阵 A 和 B,输出它们的和 A+B,
矩阵加法的规则是两个矩阵中对应位置的值进行加和,具体参照样例。
【输入格式】
第一行包含两个整数 n 和 m,表示矩阵的行数和列数 (1≤n≤100, 1≤m≤100)。
接下来 n 行,每行 m 个整数,表示矩阵 A 的元素。
接下来 n 行,每行 m 个整数,表示矩阵 B 的元素。
相邻两个整数之间用单个空格隔开,每个元素均在 1~1000 之间。
【输出格式】
n 行,每行 m 个整数,表示矩阵加法的结果。
相邻两个整数之间用单个空格隔开。
【输入样例】
3 3
1 2 3
1 2 3
1 2 3
1 2 3
4 5 6
7 8 9
【输出样例】
2 4 6
5 7 9
8 10 12
【参考程序】
#include<iostream>
using namespace std;
const int N=110;
int a[N][N], b[N][N];
int main() {
int n,m; cin>>n>>m;
for(int i=1; i<=n; i++) {
for(int j=1; j<=m; j++) {
cin>>a[i][j];
}
}
for(int i=1; i<=n; i++) {
for(int j=1; j<=m; j++) {
cin>>b[i][j];
}
}
for(int i=1; i<=n; i++) {
for(int j=1; j<=m; j++) {
cout<<a[i][j]+b[i][j]<<" ";
}
cout<<endl;
}
return 0;
}
P1216 [USACO1.5][IOI1994]数字三角形 Number Triangles
【题目】数字三角形
给定一个具有 N 层的数字三角形,从顶至底有多少条路径,
每一步可沿左斜线向下或右斜线向下,路径所经过的数字之和为路径得分,
请求出最小路径得分。
【输入格式】
第1行,一个正整数n,表示三角形的行数(n<=1500);
第2~n+1行,照描述输入三角形,所有数字均为小于2000000的整数。
【输出格式】最小路径得分,行尾有换行。
输入样例:
4
2
6 2
1 8 4
1 5 6 8
输出样例:10
样例解释:2->6->1->1
【分析】有两种走法,一种从上向下走,一种是从下往上走,每次走的时候选择得分小的路径。
第一种:从上至下,在最后一行找最小值
设二维数组 a[N][N] 存放经过每个数字时的最小路径得分,则:
a[i][j]=a[i][j]+min(a[i-1][j-1], a[i-1][j]);
但是这样发现 a[N][N] 边界值为 0,会直接导致结果错误,
所以需要初始化 a[N][N] 为极大值:a[i][j] = (1<<30); // a[i][j]=1*pow(2,30);
- 参考程序
// 从上向下走, 设置a[N][N]的值为极大值
// a[i][j]=a[i][j]+min(a[i-1][j-1], a[i-1][j]);
#include<bits/stdc++.h>
using namespace std;
const int N=1e4;
long long a[N][N];
int main() {
int n; cin>>n;
for(int i=0; i<=n; i++) {
for(int j=0; j<=n; j++) {
a[i][j]=(1<<30);
}
}
for(int i=1; i<=n; i++) {
for(int j=1; j<=i; j++) {
cin>>a[i][j];
}
}
for(int i=2; i<=n; i++) {
for(int j=1; j<=i; j++) {
a[i][j]=a[i][j]+min(a[i-1][j-1], a[i-1][j]);
}
}
int minn=(1<<30);
for(int i=1; i<=n; i++) {
if(a[n][i]<minn) minn=a[n][i];
}
cout<<minn;
return 0;
}
第二种:从下至上
设二维数组 a[N][N] 存放经过每个数字时的最小路径得分,则:
a[i][j]=a[i][j]+min(a[i+1][j], a[i+1][j+1]);
最顶端元素 a[1][1] 就是最后的最小路径得分答案。
- 参考程序
// 从下往上走 a[i][j]=a[i][j]+min(a[i+1][j], a[i+1][j+1]);
#include<bits/stdc++.h>
using namespace std;
const int N=1e4;
long long a[N][N];
int main() {
int n; cin>>n;
for(int i=1; i<=n; i++) {
for(int j=1; j<=i; j++) {
cin>>a[i][j];
}
}
for(int i=n-1; i>=1; i--) {
for(int j=1; j<=i; j++) {
a[i][j]=a[i][j]+min(a[i+1][j], a[i+1][j+1]);
}
}
cout<<a[1][1];
return 0;
}
P1002 [NOIP2002 普及组] 过河卒
【题目】过河卒
棋盘上 A(0,0) 点有一个过河卒,需要走到目标 B(n,m) 点,卒行走规则,可以向下或者向右。
同时在棋盘上的任一点有一个对方的马(C点),该马所在的点和所有跳跃一步可达的点成为对方马的控制点。
例如图中 C 点上的马可以控制 9 个点(图中 A、B 之外的黑点)卒不能通过对方马的控制点。
现在要求计算出卒从 A 点到达 B 点的路径条数。(n,m 为不超过20的整数)
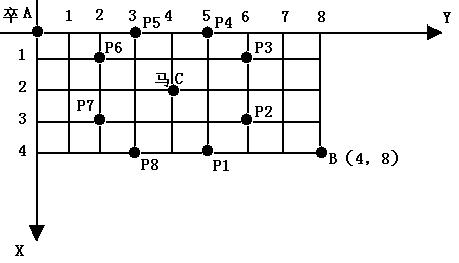
输入数据:B点坐标(n,m)以及对方马的坐标(X,Y)
输出数据:一个整数(路径的条数)
输入样例:6 6 3 3
输出样例:6
【分析】设二维数组a[i][j]表示从A点走到第i行j列位置的路径条数,则a[i][j]具有以下的性质:
(1)行坐标轴和列坐标轴上点的路径条数:a[i][0]=1, a[0][j]=1;
(2)任意一个没被马控制的坐标点(i,j),只能从(i-1,j)和(i,j-1)走到(i,j)点。
a[i][j]=a[i-1][j]+a[i][j-1];
(3)对于被马控制的坐标点,则:a[i][j]=0
根据马的走步规则,设dx,dy表示被马控制的点相对于马的坐标位移。
int dx[9]={0,2,1,-1,-2,-2,-1, 1, 2};
int dy[9]={0,1,2, 2, 1,-1,-2,-2,-1};
已知马坐标(x,y),求得被马控制点的坐标为: mx=x+dx, my=y+dy;
【程序实现】
(1)定义一个二维布尔型vis数组,表示马点(x,y)及其控制点的坐标,
一个二维数组a存储从A点走到各点的路径条数,并初始化 a, vis 数组都为0。
(2)读入B点的坐标(n,m)及对方马的坐标(x,y), 将vis中对方马点及控制点设为1。
(3)arr数组的起点初值设为1,行坐标轴上从左到右的路径条数初值设为1,直到遇到被马控制的点为止,列坐标轴上从上到下的路径条数初值设为1,直到遇到被马控制的点为止。
(4)用二重循环 i, j 分别控制第1行到第n+1行,从第1列到第m+1列,执行下列操作:
a.非马控制点:a[i][j]=a[i-1][j]+a[i][j-1];
b.马控制点:a[i][j]=0。
(5)输出 a[n][m]
【参考程序】
#include<bits/stdc++.h>
using namespace std;
const int N=110;
long long a[N][N]={1};
bool vis[N][N];
int dx[9]={0,2,1,-1,-2,-2,-1, 1, 2};
int dy[9]={0,1,2, 2, 1,-1,-2,-2,-1};
int main(){
int n,m,x,y; cin>>n>>m>>x>>y;
vis[x][y]=1;
for(int i=1; i<=8; i++){
int mx=x+dx[i],my=y+dy[i];
vis[mx][my]=1;
}
for(int i=0; i<=n; i++){
for(int j=0; j<=m; j++){
if(i) a[i][j] += a[i-1][j];
if(j) a[i][j] += a[i][j-1];
if(vis[i][j]) a[i][j]=0;
}
}
cout<<a[n][m]<<endl;
return 0;
}
P2615 [NOIP2015 提高组] 神奇的幻方
【题目】神奇的幻方
幻方是一种很神奇的 N*N 矩阵:它由数字 1,2,3,...,N*N 构成,且每行、每列及两条对角线上的数字之和都相同。
当 N为奇数时,我们可以通过下方法构建一个幻方:
首先将 1 写在第一行的中间。
之后,按如下方式从小到大依次填写每个数 K(K=2,3,...,N*N) :
若 (K-1) 在第一行但不在最后一列,则将 K 填在最后一行, (K-1) 所在列的右一列;
若 (K-1) 在最后一列但不在第一行,则将 K 填在第一列, (K-1) 所在行的上一行;
若 (K-1) 在第一行最后一列,则将 K 填在 (K-1) 的正下方;
若 (K-1) 既不在第一行,也不在最后一列,如果 (K-1) 的右上方还未填数,则将 K 填在 (K-1) 的右上方,否则将 K 填在 (K-1) 的正下方。
现给定 N,请按上述方法构造 N*N 的幻方。
输入样例:3
输出样例:
8 1 6
3 5 7
4 9 2
【参考程序】
#include<bits/stdc++.h>
using namespace std;
const int N=40;
int a[N][N];
int main() {
int n; cin>>n;
int x=1, y=n/2+1; a[x][y]=1;
for(int i=2; i<=n*n; i++){
if(x==1 && y!=n){//若 (K-1) 在第一行但不在最后一列
a[n][y+1]=i;
x=n, y=y+1;
}else if(y==n && x!=1){//若 (K-1) 在最后一列但不在第一行
a[x-1][1]=i;
x=x-1, y=1;
}else if(x==1 && y==n){//若 (K-1) 在第一行最后一列
a[x+1][y]=i;
x=x+1;
}else if(x!=1 && y!=n){//若 (K-1) 既不在第一行,也不在最后一列
if(a[x-1][y+1]==0){//如果 (K-1) 的右上方还未填数
a[x-1][y+1]=i;
x=x-1, y=y+1;
}else{
a[x+1][y]=i;
x=x+1;
}
}
}
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
cout<<setw(5)<<a[i][j];//setw(n) 设置宽度为 n
}cout<<endl;
}
return 0;
}
三维数组画立体,构建空间直角坐标系



 浙公网安备 33010602011771号
浙公网安备 33010602011771号