01.二维数组
一维数组复习
二维数组:多个一维数组的集合
格式: 类型名 数组名[常量表达式1][常量表达式2];
通常二维数组中的第一维表示行下标,第二维表示列下标。
行下标和列下标都是从0开始的。
举例:int num [4][6];
相当于一张表,每个表格对应于一个整型变量,下标变化如下表所示:
[0,0] [0,1] [0,2] [0,3] [0,4] [0,5]
[1,0] [1,1] [1,2] [1,3] [1,4] [1,5]
[2,0] [2,1] [2,2] [2,3] [2,4] [2,5]
[3,0] [3,1] [3,2] [3,3] [3,4] [3,5]
二维数组 num 由4行6列组成,共有24个元素,其中每一行都有6个元素;
如第一行的6个元素是:
num[0][0], num[0][1], num[0][2], num[0][3], num[0][4], num[0][5].
【题目】矩阵数列
给出一个 n*n 的矩阵数列,将该数列存储在二维数组 a 中,并原样输出 (n<10)。
输入样例:
4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
输出样例:
4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
- 参考程序
#include<iostream>
using namespace std;
int main(){
int n, a[10][10]; cin>>n;
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
cin>>a[i][j];
}
}
//输出程序
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
cout<<a[i][j]<<" ";
}
cout<<endl;
}
return 0;
}
int 数组长度:(对于普通题目开放的最大值了,具体还需要计算空间大小是否越界)
一维数组 N=1e8;
二维数组 N=2e4;
int 数组空间大小:
一维数组 sizeof(int)*N Byte;
二维数组 sizeof(int)*N*N Byte;
1 T = 1024 G = 2^10 G
1 G = 1024 MB
1 MB = 1024 KB
1 KB = 1024 Byte
1 Byte = 8 bit
生活中我们常见的 U盘存储器,经常会说该U盘的存储容量为 32 G,那么 32 G = 32*1024 MB,然而你却发现真实的容量会少那么一点,是因为厂家生产的时候是按照 10^3 为基数进行生产的,所以到手的 U盘实际容量为 32 G = 32*1000 MB。
二维数组的初始化
全局变量:不在 {} 内的变量
局部变量:在 {} 内的变量
整型全局变量默认初始化为 0。
整型局部变量如果没有赋初值,则会随机化数据;
整型局部变量如果部分赋值,则未赋值部分会初始化为 0。
方式一: int a[N][4]={1,2,3,4,5,6,7};
相当于: a[0][0]=1, a[0][1]=2, a[0][2]=3, a[0][3]=4,
a[1][0]=5, a[1][1]=6, a[1][2]=7, a[1][3]=0,
a[2][0]=0, ..., a[i][j]=0, ...
方式一:
1 2 3 4
5 6 7 0
0 0 0 0
0 ... 0
方式二: int a[N][4]={{1,2,3}, {4,5,6}, {7}};
相当于: a[0][0]=1, a[0][1]=2, a[0][2]=3, a[0][3]=0,
a[1][0]=4, a[1][1]=5, a[1][2]=6, a[1][3]=0,
a[2][0]=7, ..., a[i][j]=0, ...
方式二:
1 2 3 0
4 5 6 0
7 0 0 0
0 ... 0
#include<iostream>
using namespace std;
int main(){
int num[4][3] = {{45,6,78}, {43,57,68}, {15,65,72}, {15,47,28}};
for(int i=0; i<4; i++){
for(int j=0; j<3; j++) {
cout<<num[i][j]<<" "; // 猜猜我会输出什么
}cout<<endl;
}
return 0;
}
二维数组的使用
二维数组的使用与一维数组类似: 数组名[下标1][下标2]
注意:
使用数组时特别注意下标不能越界。
使用二维数组时,区分处理行数据、列数据,还是处理所有数据的行列下标。
一般使用两层循环来控制二维数组,外层控制行数,内层控制列数。
【题目】对角线元素和
输入一个数据 n,接下来输入一个 n*n 方阵,输出方阵对角线的和。
输入样例:
4
1 2 3 4
1 2 3 4
1 2 3 4
4 3 2 1
输出样例:
7 13
【分析】对角线元素和
i j --- i 表示行,j 表示列
00 01 02 03
10 11 12 13
20 21 22 23
30 31 32 33
对角线:有两条,找到对应的规律即可
左上角到右下角:i==j
左下角到右上角:i+j==n-1
int sum1=0,sum2=0;
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
if(i==j) sum1 += a[i][j];
if(i+j==n-1) sum2 += a[i][j];
}
}
cout<<sum1<<" "<<sum2;
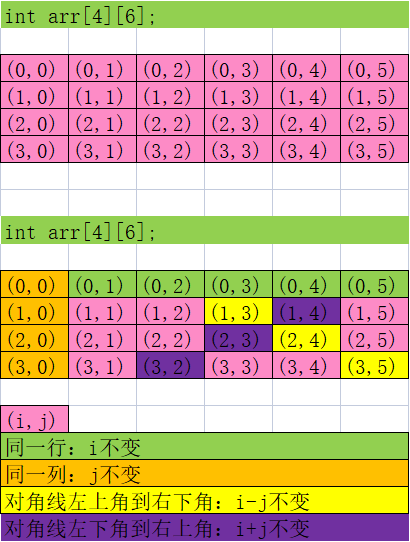
二维数组重点知识:用于地图找规律
i j --- i 表示行,j 表示列
00 01 02 03
10 11 12 13
20 21 22 23
30 31 32 33
依据下标找到规律:
同一行:i 是定值
同一列:j 是定值
左上角到右下角:i-j 是定值
左下角到右上角:i+j 是定值
【题目】图像旋转
输入一个 n 行 m 列的黑白图像的每个像素点灰度,每个元素均在 0~255之间,将它顺时针旋转 90° 后输出(1<=n, m<=100)。
输入样例:
3 3
1 2 3
4 5 6
7 8 9
输出样例:
7 4 1
8 5 2
9 6 3
【分析】图像旋转
将转变前后图像用二维数组下标的形式展示出来,找到规律。
i j --- i 表示行,j 表示列,如:3 行 4 列
旋转前:a[i][j]
00 01 02 03
10 11 12 13
20 21 22 23
旋转后:b[i][j]
20 10 00
21 11 01
22 12 02
23 13 03
程序实现:
#include<iostream>
using namespace std;
const int N=100;
int a[N][N], b[N][N];
int main(){
int n,m; cin>>n>>m;
for(int i=0; i<n; i++){
for(int j=0; j<m; j++){
cin>>a[i][j];
}
}
for(int i=0; i<m; i++){
for(int j=0; j<n; j++){
b[i][j] = a[n-1-j][i];
cout<<b[i][j]<<" ";
}cout<<endl;
}
return 0;
}
【题目】杨辉三角
杨辉三角是一个由数字排列成的三角形数列表,给一个正整数 n,请输出杨辉三角形的前 n 行(n<20)。
输入样例:
7
输出样例:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
【分析】杨辉三角
杨辉三角的数字是有规律的:
从第 3 行开始,每行第 1 个和最后一个值为 1,其它为其上方和左上方数字和。
设二维数组 a[i][j] 存储坐标为 i-1,列坐标为j-1位置上元素值,则
a[i][j] = a[i-1][j-1] + a[i-1][j];
每个元素值由其左上方和上方元素求和得到。
因此,可以一行一行的求得元素值。
- 参考程序
#include<bits/stdc++.h>
using namespace std;
int main() {
int n, a[20][20]={0}; cin>>n;
a[1][1]=1;
for(int i=2; i<=n; i++){
for(int j=1; j<=n; j++){
a[i][j] = a[i-1][j]+a[i-1][j-1];
}
}
for(int i=1; i<=n; i++){
for(int j=1; j<=i; j++){
cout<<a[i][j]<<" ";
}
cout<<endl;
}
return 0;
}
【题目】S形方阵
读入两个数,代表 n 行 m 列,然后从 (0,0) 开始 S 形输出 1~n*m 方阵,如下样例 (0<=n, m<25)。
输入样例:
3 4
输出样例:
1 2 3 4
8 7 6 5
9 10 11 12
【分析】S形方阵
找到每一行的起始位置与终点位置,发现每一行运动结束后方向会发生变化,奇数行从左向右递增,偶数行从右往左递增。
那么可以建立一个二维数组存储答案,设置一个计数器 cnt=0;
每走一格 cnt+1,并存储赋值给当前格子,当一行结束后再逆方向计数;
最后输出二维数组。
const int N=25;
int a[N][N];
int n, m, count=0; cin>>n>>m;
for(int i=0; i<n; i++){
if(i%2==0){ //如果是偶数行
for(int j=0; j<m; j++) a[i][j] = ++count;
}else{ //如果是奇数行
for(int j=m-1; j>=0; j--) a[i][j] = ++count;
}
}
【题目】蛇形方阵
在 n*n 的方阵中填入1,2,3,...,n*n (n<25),要求填成如下形式的蛇形方阵。
每个数据占 5 个宽度。
输入样例:
4
输出样例:
10 11 12 1
9 16 13 2
8 15 14 3
7 6 5 4
【分析】蛇形方阵
直接输出蛇形方阵是做不到的,如果将数字按蛇形方阵形式存入二维数组中,输出就很容易了。
设二维数组 a[N][N] 存放蛇形方阵,设变量 x 表示行,y 表示列;
那么从 x=1,y=n 开始写入数字 1,然后写入顺序是下、左、上、右。
但是要注意写入时下标不能溢出。
#include<iostream>
#include<iomanip> // setw(5)
using namespace std;
const int N=1e4;
int a[N][N]; //全局变量,数组初始化为 0
int main() {
int n; cin>>n;
int x=0, y=n, cnt=0;
while(cnt<n*n) {
while(x+1<=n && a[x+1][y]==0) a[++x][y]=++cnt; //向下
while(y-1>=1 && a[x][y-1]==0) a[x][--y]=++cnt; //向左
while(x-1>=1 && a[x-1][y]==0) a[--x][y]=++cnt; //向上
while(y+1<=n && a[x][y+1]==0) a[x][++y]=++cnt; //向右
}
for(int i=1; i<=n; i++) {
for(int j=1; j<=n; j++) {
cout<<setw(5)<<a[i][j]; //设置每个数据占 5 个宽度
} cout<<endl;
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号