3.10前缀和与差分
3.10前缀和与差分

一维前缀和:一维数组区间求和
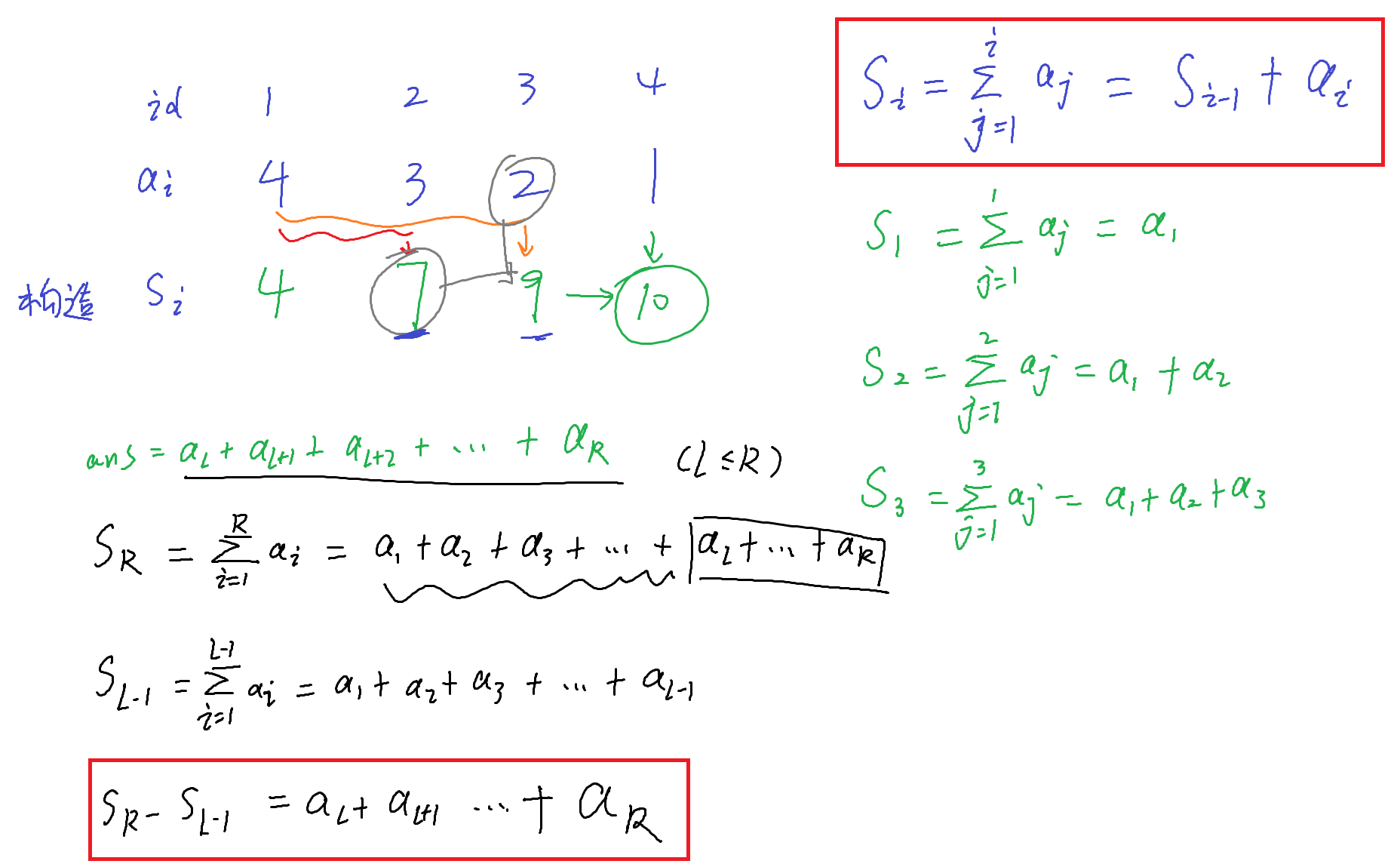
给定长度为 n 的序列 a[1],a[2]...a[n], 则 sum[i] = a[1]+a[2]...+a[i] = sum[i-1]+a[i].
区间和 [l,r]=sum[r]-sum[l-1]
【题目描述】
给定长度为 \(n\) 的序列 \(a[1],a[2],...,a[n]\),给定 \(q\) 个询问 \([l,r]\),输出 \([l,r]\) 的区间和。
数据范围: \(n,q \leq 10^5\)
输入格式:
第一行输入 \(n, q\) ;
第二行输入序列 \(a[1],a[2],...,a[n]\);
接下来 \(q\) 行,每行两个数据,分别对应 \(l, r\)。
输出格式: 输出 \(q\) 行,表示 \([l, r]\) 区间和。
| 输入样例 | 输出样例 |
|---|---|
10 5 1 2 3 4 5 5 4 3 2 1 1 6 3 8 1 10 5 5 1 3 | 20 24 30 5 6 |
方法1:暴力计算每个询问 \([l,r]\),时间复杂度: \(O(q ×n)\)
方法2:前缀和,输出每个询问 \([l,r]\), 时间复杂度: \(O(n + q)\)
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N], sum[N];
int main(){
int n,m,l,r; scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
for(int i=1; i<=n; i++){ //前缀和预处理
sum[i] = sum[i-1]+a[i];
}
for(int i=1; i<=m; i++){
scanf("%d%d", &l, &r);
printf("%d\n", sum[r]-sum[l-1]);
}
return 0;
}
二维前缀和:二维矩阵区间求和
给定一个矩阵 \(s[i][j]\),\(sum[i][j]\)是矩阵 \(s[1...i][1...j]\) 的和。
使用二维前缀和可以在 \(O(1)\) 时间内求一个矩阵和。

【题目描述】
给定一个 \(n*m\) 大小的矩阵 \(a\),有 \(q\) 次询问,每次询问给定 \(x1,y1,x2,y2\) 四个数,
求以 \((x1,y1)\) 为左上角坐标和 \((x2,y2)\) 为右下角坐标的子矩阵的所有元素和。
注意仍然包含左上角和右下角的元素。
数据范围: \(n,m,q<=10^4\)
输入格式:
第一行输入 \(n, m, q\) ;
接下来 \(n\) 行, 每行 \(m\) 个数据,表示矩阵元素;
接下来 $q $ 行,每行 \(4\) 个数据,分别对应 \(x1,y1,x2,y2\)。
输出格式: 输出 \(q\) 行,表示以 \((x1,y1)\) 为左上角坐标和 \((x2,y2)\) 为右下角坐标的子矩阵的所有元素和。
| 输入样例 | 输出样例 |
|---|---|
4 5 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 1 2 2 1 1 3 3 2 2 4 4 1 1 4 5 2 4 4 5 |
6 18 27 60 27 |
#include<iostream>
using namespace std;
const int N=1e4+10;
int a[N][N], sum[N][N];
int n,m,q,x1,y1,x2,y2,ans=0;
int main(){
scanf("%d%d%d", &n, &m, &q);
for(int i=1; i<=n; i++){
for(int j=1; j<=m; j++){
scanf("%d", &a[i][j]); // 二维前缀和预处理
sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j];
}
}
for(int i=1; i<=q; i++){
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
ans = sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1];
printf("%d\n", ans);
}
return 0;
}
一维差分:一维数组区间修改
差分:每个元素与前一个元素的差值
如原数组 arr: 1 2 3 4 5
则差分为 dif: 1 1 1 1 1 ( dif[] 的前缀和即为 arr[])
单点修改 arr[i]+add:
若将 arr[1]+1, 则 arr: 1 3 3 4 5
则差分数组 dif: 1 2 0 1 1,
只会改变自己和后一个数, 即 dif[i] += add, dif[i+1] -= add.
区间修改 [l,r] 增加 add:
若将 arr 数组 [2,4] 每个元素+1, arr: 1 3 4 5 5
则差分数组 dif: 1 2 1 1 0,
只会改变 dif[l] 和 dif[r] 后一个数,即 dif[l] += add, dif[r+1] -= add.

- P2367 语文成绩
【题目描述】
给定长度为 \(n\) 的序列 \(a[1],a[2],...,a[n]\),初始都为 0,
接着 \(m\) 个操作 \(l,r,add\) ,表示给 \(a\) 数组 \([l,r]\) 区间内的每个数加 \(add\),
给定 \(q\) 个询问输出 \(a[i]\) 的值。
数据范围: \(n,m,q≤1e5\)
| 输入样例 | 输出样例 |
|---|---|
10 5 10 1 2 1 2 2 2 2 2 3 5 8 4 2 10 5 1 2 3 4 5 6 7 8 9 10 | 1 11 5 5 9 9 9 9 5 5 |
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e6+10,INF=0x3f3f3f3f;
int n,m,q,a[N],b[N];
int main(){
scanf("%d%d%d",&n,&m,&q); int l,r,add;
while(m--){
scanf("%d%d%d",&l,&r,&add);
b[l] += add;
b[r+1] -= add;
}
for(int i=1; i<=n; i++) b[i]=b[i-1]+b[i];
while(q--){
cin>>l;
printf("%d ",b[l]);
}
return 0;
}
二维差分:二维矩阵区间修改
有一个二维矩阵
1 2 4 3
5 1 2 4
6 3 5 9
对应的二维差分矩阵如下:
1 1 2 -1
4 -5 -1 3
1 1 1 2
【题目描述】
输入一个 \(n\) 行 \(n\) 列的整数矩阵,再输入 \(q\) 个操作,
每个操作包含五个整数 \(x1,y1,x2,y2,c\),
其中 \((x1, y1)\) 和 \((x2, y2)\) 表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上 \(c\)。
请你将进行完所有操作后的矩阵输出。
输入格式:
第一行包含整数 \(n,m,q\)。
接下来 \(n\) 行,每行包含 \(m\) 个整数,表示整数矩阵。
接下来 \(q\) 行,每行包含 \(5\) 个整数 \(x1,y1,x2,y2,c\),表示一个操作。
输出格式: 共 \(n\) 行,每行 \(m\) 个整数,表示所有操作进行完毕后的最终矩阵。
| 输入样例 | 输出样例 |
|---|---|
3 4 3 1 2 2 1 3 2 2 1 1 1 1 1 1 1 2 2 1 1 3 2 3 2 3 1 3 4 1 | 2 3 4 1 4 3 4 1 2 2 2 2 |
数据范围:
#include<iostream>
using namespace std;
const int N=1e4+10;
int a[N][N], sum[N][N], dif[N][N];
int n,m,q,x1,y1,x2,y2,c;
int main(){
scanf("%d%d%d", &n, &m, &q);
for(int i=1; i<=n; i++){
for(int j=1; j<=m; j++){
scanf("%d", &a[i][j]);
dif[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1];
}
}
for(int i=1; i<=q; i++){
scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
dif[x1][y1] += c;
dif[x1][y2+1] -= c;
dif[x2+1][y1] -= c;
dif[x2+1][y2+1] += c;
}
for(int i=1; i<=n; i++){
for(int j=1; j<=m; j++){
dif[i][j] += dif[i-1][j]+dif[i][j-1]-dif[i-1][j-1];
printf("%3d", dif[i][j]);
}printf("\n");
}
return 0;
}
洛谷练习题目
- P8218 【深进1.例1】求区间和
- P3397 地毯
- P2367 语文成绩
- CF276C Little Girl and Maximum Sum
- P5638 【CSGRound2】光骓者的荣耀
- P1115 最大子段和
- P1719 最大加权矩形
- P3406 海底高铁
- P2004 领地选择
三维差分
差分数组D[][][]是三维的
把三维差分想象成在立体空间上的操作。一维的区间是一个线段,二维是矩形,那么三维就是立体块。
一个小立体块有8个顶点,所以三维的区间修改,需要修改8个D[][][]值。
三维差分的区间修改
D[x1][y1][z1] += d; //前:左下顶点,即区间的起始点
D[x2+1][y1][z1] -= d; //前:右下顶点的右边一个点
D[x1][y1][z2+1] -= d; //前:左上顶点的上面一个点
D[x2+1][y1][z2+1] += d; //前:右上顶点的斜右上方一个点
D[x1][y2+1][z1] -= d; //后:左下顶点的后面一个点
D[x2+1][y2+1][z1] += d; //后:右下顶点的斜右后方一个点
D[x1][y2+1][z2+1] += d; //后:左上顶点的斜后上方一个点
D[x2+1][y2+1][z2+1] -= d; //后:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号