3.6排序&查找
3.6排序&查找
1. 排序认识
排序是指将一个无序数列,经过一些处理,变成一个有序数列的过程。
有序序列也可以形象化描述为:
当对于任意 i, 有 a[i] ≤ a[i+1],那么称数列 {a[i]} 是一个非降序列或递增序列。
当对于任意 i, 有 a[i] ≥ a[i+1],那么称数列 {a[i]} 是一个非增序列或递减序列。
稳定排序:对于 i<j, 有 a[i]=a[j],排序后仍然满足 a[i] 在 a[j] 前面,则称排序为稳定排序。
逆序对:对于 i<j, 有 a[i]>a[j],则称 a[i],a[j] 为一对逆序对。
排序的过程就是不断减少逆序对的过程。
而对于排序的方法按照基本原理主要分两种:
基于比较的排序方法:冒泡排序,选择排序,插入排序,归并排序,堆排序,快速排序、希尔排序。
非基于比较的排序方法:计数排序、基数排序、桶排序。
2. 冒泡排序
它重复地走访过要排序的数列,一次比较两个相邻的元素,如果它们的顺序错误就把它们交换过来。
走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
假设要升序排序:也就是 a[i] ≤ a[i+1],那么如果出现 a[i]>a[i+1] 的时候就交换。
(这个假设思想是一种反向思考问题的方式,很不错哦!)

//冒泡排序:最大的下沉到最后,小的向上冒泡
void BubbleSort(int arr[], int l, int r){
for(int i=r; i>=l; i--)
for(int j=l; j<i; j++)
if(a[j]>a[j+1]) swap(a[j],a[j+1]);
}
- 会发现一个有趣的事情就是交换的次数就是逆序对的数量。
冒泡排序小优化:如果当前没有出现交换,那么证明元素已经有序了。
void BubbleSort(int arr[], int l, int r){
for(int i=r; i>=l; i--){
bool flag=1;
for(int j=l; j<i; j++)
if(a[j]>a[j+1]) swap(a[j],a[j+1]), flag=0;
if(flag) break;
}
}
3. 选择排序
初始时在序列中找到最大元素,放到序列的末尾位置作为已排序序列;
然后,再从剩余未排序元素中继续寻找最大元素,放到未排序序列的末尾。
以此类推,直到所有元素均排序完毕。
这里我们选择记录最大值所在下标,一次遍历完成后,对比下标是否发生变化,如果发生变化,就交换;
(每一次比较后进行交换与冒泡相差无几,不推荐)

//选择排序:每次选择最大的放在最后
void SelectSort(int a[], int l, int r){
for(int i=r; i>=l; i--){
int k=i;
for(int j=l; j<i; j++)
if(a[k]<a[j]) k=j;
if(k!=i) swap(a[k],a[i]);
}
}
4. 插入排序
每步将一个待排序的纪录,按其关键码值的大小插入前面已经排序的文件中适当位置上,直到全部插入完为止。

//插入排序:向左边有序序列中插入一个元素
void InsertSort(int a[], int l, int r){
for(int i=l; i<=r; i++){
int k=i; //记录现在插入元素的位置
for(int j=i; j>=l; j--)
if(a[k]<a[j]) swap(a[k], a[j]), k=j;
}
}
5. 快速排序
快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。
它采用了一种分治的策略,通常称其为分治法(Divide-and-ConquerMethod)。
该方法的基本思想是:将序列分成左右两个部分,使得左边部分的元素都比右边部分小,再继续递归左右两个部分。
算法步骤:
- 先从数列中取出一个数作为基准数。
- 将比这个基准数大的数放到右边,小于或等于它的数放到它的左边。
- 再对左右区间重复第二步,直到各区间只有一个数。
注意:选择基准值的时候,如果是随机选择,那么时间复杂度为 O(nlogn)
但是很难做到完全随机,于是我们会规定选择的位置
- 最左侧,最右侧,中间值,随机值:a[l], a[r], a[l+r>>1], a[rand()%(r-l+1)+l]
- 或者选择前进行随机打乱,以防止专门的数据卡时(比如:本身就是一个升序序列)
- random_shuffle(a, a+n); // 随机打乱 a[0~n-1]
- 下图为选择最右侧值的情况


// 快速排序:选择一个基准值base, <=base, >=base
// 递归实现要素
// 1. 递归函数:QuickSort(l,r)
// 2. 递归关系:l j,i r --- QuickSort(l,j), QuickSort(i,r)
// 3. 递归出口:l>=r
void QuickSort(int a[],int l,int r){
if(l>=r) return;
int i=l, j=r, b=a[l+r>>1];
while(i<j){
while(a[i] < b) i++;
while(a[j] > b) j--;
if(i<=j) swap(a[i],a[j]), i++, j--;
}
QuickSort(a,l,j), QuickSort(a,i,r);
// if(j>=k) QuickSort(a,l,j); // 求第 k 小的元素
// if(i<=k) QuickSort(a,i,r);
}
求第 k 小的元素也可以使用 nth_element 函数
nth_element(begin, begin + k_th, end);
int a[] = {1,6,7,2,3,4,5,8,9,10};
nth_element(a, a+5, a+10);
printf("%d", a[5]); // 6, 下标从 0 开始
但是对于很多的竞赛选手而言,排序知识不过是一些比较基础的能力罢了,没必要耗费
过多的时间在这个上面,于是使用C++中的STL里面的 sort排序就成为了大家的最爱,
下面就对 sort排序进行讲解
首先看一个问题:给定一个数列 {5,2,6,4,3,1,9,0,8,7}, 现在要求对其进行升序排序。
#include<iostream>
#include<algorithm>// sort
using namespace std;
bool cmp(int a,int b){ //自定义排序规则,按照降序排序
return a>b;
}
int main(){
int a[]={5,2,6,4,3,1,9,0,8,7};
int n= sizeof(a)/sizeof(int);
sort(a, a+n); //内部封装快速排序,默认按照升序排序
for(int i=0; i<n; i++) cout<<a[i]<<" "; cout<<endl;
sort(a, a+n, cmp);
for(int i=0; i<n; i++) cout<<a[i]<<" "; cout<<endl;
sort(a, a+n, greater<int>()); // 降序
for(int i=0; i<n; i++) cout<<a[i]<<" "; cout<<endl;
sort(a, a+n, less<int>()); // 升序
for(int i=0; i<n; i++) cout<<a[i]<<" "; cout<<endl;
return 0;
}
STL的 sort() 算法,数据量大时采用 Quick Sort,分段递归排序。一旦分段后的数据量小于某个阈值,为避免 Quick Sort的递归调用带来过大的额外开销,就改用Insertion Sort(插入排序)。如果递归层次过深,还会改用 Heap Sort。
由于多数情况下是对大数据进行排序,所以我们姑且认为sort就是内部封装Quick Sort。
6. 归并排序
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法。
该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
将已有序的子序列合并,得到完全有序的序列;
即先使每个子序列有序,再使子序列段间有序。
若将两个有序表合并成一个有序表,称为二路归并。
归并排序是一种稳定的排序方法。

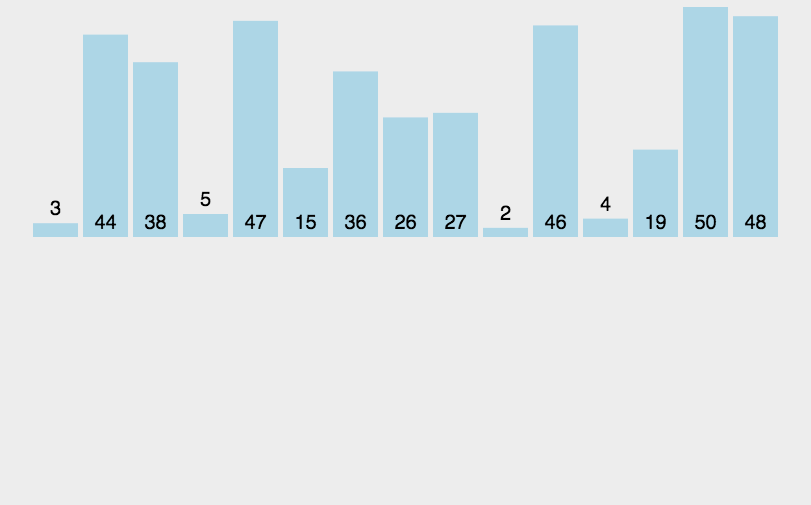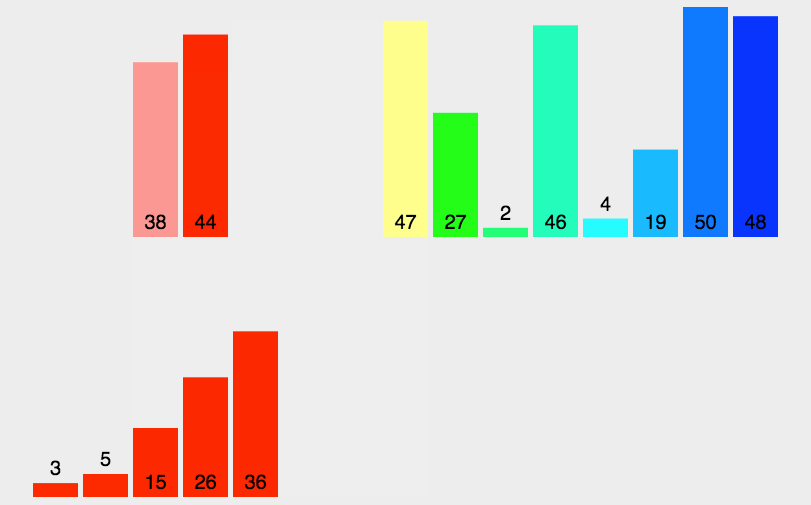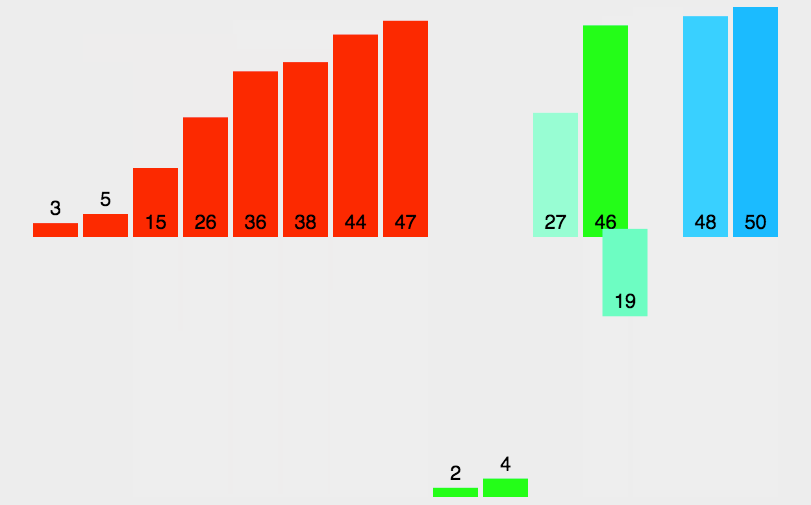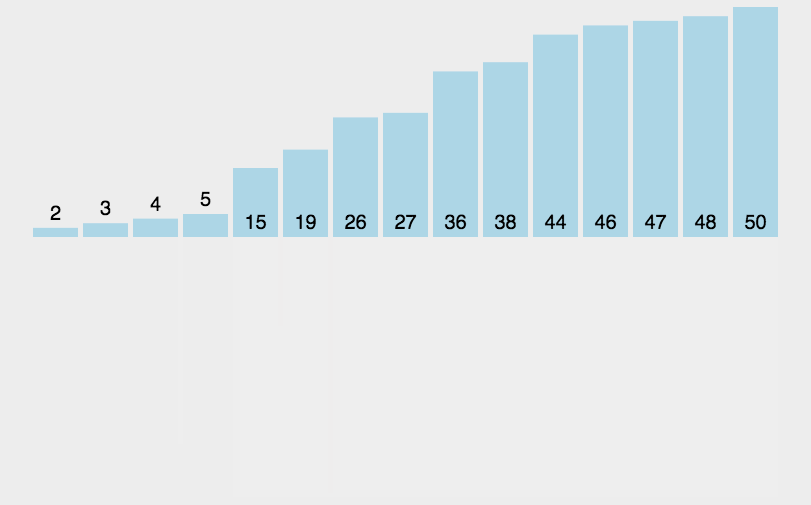
// 归并排序: 将数据递归均分成两部分,直到数据元素个数为 1
// 1. 递归函数:MergeSort(l,r)
// 2. 递归出口:l>=r
// 3. 递归关系:[l,r] = [l, mid] + [mid+1, r] --- MergeSort(l,mid), MergeSort(mid+1,r);
int temp[N],cnt=0;// cnt逆序对数量
void MergeSort(int a[], int l, int r){
if(l>=r) return;
int mid=(l+r)/2, i=l, j=mid+1, p=0;
MergeSort(a, l, mid); MergeSort(a, mid+1, r); // 递归拆分
// 合并:两个有序序列合并,需要开一个临时空间 temp[]
while(i<=mid && j<=r){
if(a[i]<=a[j]) temp[++p]=a[i++];
else temp[++p]=a[j++], cnt+=mid-i+1;// 逆序对计数
}
while(i<=mid) temp[++p]=a[i++];
while(j<=r) temp[++p]=a[j++];
for(int i=1; i<=p; i++) a[l++]=temp[i];
}
7. 计数排序
对各个元素出现次数进行计数,最后依次输出。(桶距为 1 时的桶排序)

int main(){
int n, minn=2e9, maxn=0; //需要给最大值和最小值分别赋极端值
scanf("%d", &n);
for(int i=1; i<=n; i++){
int x; scanf("%d", &x); arr[x]++;
if(minn>x) minn=x;
if(maxn<x) maxn=x; //最大值和最小值决定了桶的范围
}
for(int i=minn; i<=maxn; i++){
while(arr[i]--) printf("%d ", i);
}
return 0;
}
还有很多排序,如改进选择排序的希尔排序、基数排序、堆排序....。
8. 顺序查找
通过遍历无序数组,一个一个对比数组中的值与目标值是否相同。
对于数据没有任何要求,但是时间复杂度 O(n)。
9. 二分查找
二分查找是基于一个有序序列而言,使用二分查找前需要对该序列排序处理。
二分查找,又称折半查找,基本思想是将 n 个元素分成大致相等的两部分,
取 a[n/2] 与 x 做比较,如果 x=a[n/2],则找到 x,算法中止;
如果 x<a[n/2],则只要在数组a的左半部分继续搜索 x,
如果 x>a[n/2],则只要在数组a的右半部搜索 x。
// 整数二分
// 找左边界:区间 [l,r] 被划分为 [l, mid] [mid+1, r]
int left(int l,int r){
while(l < r){
int mid = l+r >> 1;
if(check(mid)) r=mid;
else l=mid+1;
}
return l;
}
// 找右边界:区间 [l,r] 被划分为 [l, mid-1] [mid, r]
int right(int l,int r){
while(l < r){
int mid = l+r+1 >> 1;
if(check(mid)) l=mid;
else r=mid-1;
}
return l;
}
// 小数二分
double sqrt2(double n){
double l=0, r=n;
while(r-l > eps){
double mid=(l+r)/2;
if(mid*mid >= n) r=mid;
else l=mid;
}
return l;
}
由于冒泡排序/选择排序/插入排序的时间复杂度均为 \(O(n^2)\),一般不使用。
快速排序的时间复杂度为 \(O(nlogn)\),快是快,但不稳定且会被卡,不过sort挺好。
归并排序的时间复杂度为 \(O(nlogn)\),快且稳定,推荐。
计数排序,对数据范围大小要求很高,不过计数思想要掌握。
顺序查找枚举暴力的首选,其外无用;二分查找神器,有趣的思想,一定要会。
总结:解决题目时,可以使用sort(内部封装快排),但是注意要不要稳定排序,可以结合结构体实现稳定排序。
但是不要认为sort天下第一,毕竟别人写的不如自己的,归并神器要会。
其余 \(O(n^2)\) 的排序掌握原理,自己能实现即可。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号