CSP 2019 入门组第一轮
CSP 2019 入门组第一轮
一、单项选择题
(共15题,每题2分,共计30分)
-
中国的国家顶级域名是()
A. .cn
B. .ch
C. .chn
D. .china
解析:
cn - 中国国家顶级域名
com - 工、商、金融等企业
edu - 教育机构
gov - 政府部门
org - 各种非盈利性的组织
答案:A
其他更多 推荐-百度百科-域名 -
二进制数 11 1011 1001 0111 和 01 0110 1110 1011 进行逻辑与运算的结果是()。
A. 01 0010 1000 1011
B. 01 0010 1001 0011
C. 01 0010 1000 0001
D. 01 0010 1000 0011
解析:题目中表述错误,应该是求按位与,如果说是求逻辑与的话结果就是:1,但是选项又没有。
&& 逻辑与,同真为真 a&&b==1 (a=b=1)
|| 逻辑或, 同假为假 a||b==0 (a=b=0)
! 非,非真即假
& 按位与,同真为真 1001 & 1100 = 1000
| 按位或,同假为假 1001 | 1100 = 1101
^ 异或,相异为真 1001 ^ 1100 = 0101
~ 取反,真假互换 ~1001 = 0110
<< 左移,1001<<2 = 100100
>> 右移,1001>>2 = 0010
答案:D
-
一个32位整型变量占用()个字节。
A. 32
B. 128
C. 4
D. 8
解析:1Byte=8bit, 32bit=4Byte
答案:C -
若有如下程序段,其中s、a、b、c均已定义为整型变量,且a、c均已赋值(c大于0)
s=a;
for(b=1; b<=c; b++) s=s-1;
则与上述程序段功能等价的赋值语句是()
A. s = a - c;
B. s = a - b;
C. s = s - c;
D. s = b - c;
解析:for循环1~c,也就是c次,那么就是 s-c; 又 s 初始化为 a, 所以:s=a-c.
答案:A -
设有100个已排好序的数据元素,采用折半查找时,最大比较次数为()
A. 7
B. 10
C. 6
D. 8
解析:折半查找其实就是二分查找,每一次查找的都是当前内容的一半,\(2^k>=100, k>=7\),所以结果为 7。
答案:A -
链表不具有的特点是()
A. 插入删除不需要移动元素
B. 不必事先估计存储空间
C. 所需空间与线性表长度成正比
D. 可随机访问任一元素
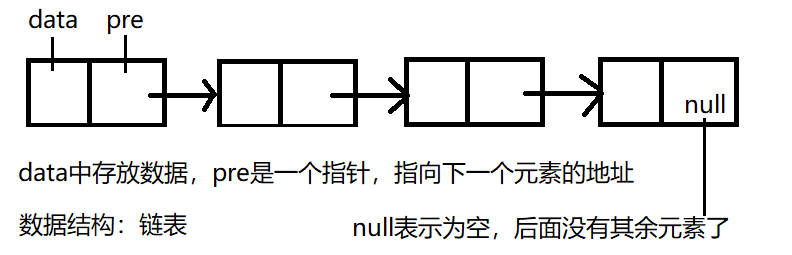
![image]()
链表特点:
插入删除元素都不需要移动元素,直接修改元素的pre指针指向的方向即可。
不需要事先估计存储空间,新增元素可以重新开存储空间,再将链表最后的指针指向该空间的地址即可。
链表访问其中元素的时候是从头到尾进行遍历,直到找到该元素,不能像数组那样通过下标直接访问。
答案:D -
把 8 个同样的球放在 5 个同样的袋子里,允许有的袋子空着不放,问共有多少种不同的分法?()
提示:如果8个球都放在一个袋子里,无论是哪个袋子,都只算同一种分法。
A. 22
B. 24
C. 18
D. 20
解析:
放入1个袋子:00008
放入2个袋子:00017, 00026, 00035, 00044
放入3个袋子:00116, 00125, 00134, 00224, 00233
放入4个袋子:01115, 01124, 01133, 01223, 02222
放入5个袋子:11114, 11123, 11222
答案:18 -
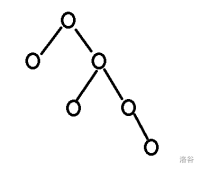
一棵二叉树如右图所示,若采用顺序存储结构,即用一维数组元素存储该二叉树中的结点(根结点的下标为1,若某结点的下标为i ,则其左孩子位于下标2i处、右孩子位于下标2i+1处),则该数组的最大下标至少为()。
![image]()
A. 6
B. 10
C. 15
D. 12
解析:根据满二叉树的特点,知道最后一个叶子节点的位置:\(2^k-1\), 所以 \(2^4-1=15\). 或者按照题中所述,\(2i+1\) 必为奇数。
答案:C -
100以内最大的素数是()。
A. 89
B. 97
C. 91
D. 93
解析:先找最大,再看素数,哎呀那不就是97嘛!或者你直接求100以内的最大素数,但是好像有点费时。 -
319和377的最大公约数是()。
A. 27
B. 33
C. 29
D. 31
解析:选择题,直接带答案进入计算即可,或者辗转相除法
辗转相除法原理:
a/b = q...r
a,b的最大公约数 和 b,r的最大公约数相同
所以 gcd(a, b) = gcd(b, r);
377 / 319 = 1...58
319 / 58 = 5...29
58 / 29 = 2...0
所以 a,b的最大公约数就是 29.
-
新学期开学了,小胖想减肥,健身教练给小胖制定了两个训练方案。
方案一:每次连续跑3公里可以消耗300千卡(耗时半小时);
方案二:每次连续跑5公里可以消耗600千卡(耗时1小时)。
小胖每周周一到周四能抽出半小时跑步,周五到周日能抽出一小时跑步。
另外,教练建议小胖每周最多跑21公里,否则会损伤膝盖。
请问如果小胖想严格执行教练的训练方案,并且不想损伤膝盖,每周最多通过跑步消耗多少千卡?()
A. 3000
B. 2500
C. 2400
D. 2520
解析:选择合适的策略:最小的代价获取最多的利益,由于连续跑5公里消耗能量效率高,作为首选。
周五、六、七执行方案二:3天可跑 3x5 公里,消耗 600x3 千卡;
还可以跑 21-3x5=6公里,执行2次方案1,2天可消耗 300x2 千卡;
所以最后消耗能量:600x3+300x2=2400. -
—副纸牌除掉大小王有52张牌,四种花色,每种花色13张。
假设从这52张牌中随机抽取13张纸牌,则至少()张牌的花色一致。
A. 4
B. 2
C. 3
D. 5
解析:至少几张花色不一致,则每次选则都选择当前未被选择过的花色,但是由于本次未被选择,那么下次选择也会被加入到选择的序列,所以对于花色的选择无先后之分。
花色: 1 2 3 4
选择: 1 2 3 4
5 6 7 8
9 10 11 12
13
所以至少4种花色一致
-
—些数字可以颠倒过来看,例如 0、1、8 颠倒过来还是本身,6 颠倒过来是 9, 9颠倒过来看还 是6,其他数字颠倒过来都不构成数字。类似的,一些多位数也可以颠倒过来看,比如 106 颠倒过来是 901。假设某个城市的车牌只由5位数字组成,每一位都可以取 0 到 9。请问这个城市最多有多少个车牌倒过来恰好还是原来的车牌?()
A. 60
B. 125
C. 75
D. 100
解析:
![image]()
第1位可放:0 1 8 6 9
第2位可放:0 1 8 6 9
中间可放:0 1 8
所以结果为:5x5x3=75 -
假设一棵二叉树的后序遍历序列为 DGJHEBIFCA,中序遍历序列为 DBGEHJACIF,则其前序遍历序列为()。
A. ABCDEFGHIJ
B. ABDEGHJCFI
C. ABDEGJHCFI
D. ABDEGHJFIC
解析:
![image]()
先根据题目信息还原这棵树,再按照前序遍历顺序来推导
![image]()
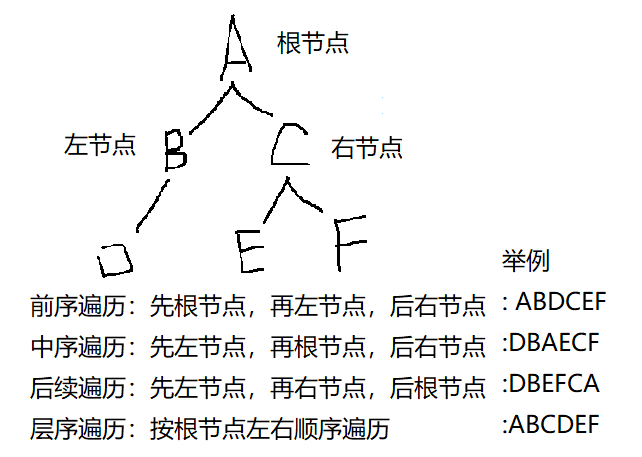
前序遍历:先根节点,再左节点,后右节点
中序遍历:先左节点,再根节点,后右节点
后续遍历:先左节点,再右节点,后根节点
层序遍历:按根节点左右顺序遍历
问题:后序遍历序列为DGJHEBIFCA,
中序遍历序列为DBGEHJACIF,则其前序遍历序列为()
- 根据后序遍历确定根节点
- 根据中序遍历确定其余节点在左子树,还是右子树
- 对左右子树循环步骤1,2
- 对最后还原的树进行检查
- 以下哪个奖项是计算机科学领域的最高奖?()
A. 图灵奖
B. 鲁班奖
C. 诺贝尔奖
D. 普利策奖
解析:这就是个记忆性问题:计算机科学领域的最高奖是图灵奖,建议百度一下图灵这个人物。
阿兰·麦席森·图灵(Alan Mathison Turing ,1912年6月23日-1954年6月7日),英国著名的数学家和逻辑学家,被称为计算机科学之父、人工智能之父,是计算机逻辑的奠基者,提出了“图灵机”和“图灵测试”等重要概念。曾协助英国军方破解德国的著名密码系统“谜”(Enigma),帮助盟军取得了二战的胜利。人们为纪念其在计算机领域的卓越贡献而设立“图灵奖”。图灵同时还是著名的男同性恋者之一,但不幸因为其性倾向而遭到当时的英国政府迫害,最终自杀。2013年12月24日,英国女王伊丽莎白二世宣布赦免图灵。
二、阅读程序
(除特殊说明外,判断题1.5分,选择题3分,共计40分)
程序输入不超过数组或字符串定义的范围;
判断题正确填√,错误填×;
第 16 题(本题共 12 分)
1. #include <cstdio>
2. #include <cstring>
3. using namespace std;
4. char st[100];
5. int main() {
6. scanf("%s", st);
7. int n = strlen(st);
8. for (int i = 1; i <= n; ++i) {
9. if (n % i == 0) {
10. char c = st[i - 1];
11. if (c >= 'a')
12. st[i - 1] = c - 'a' + 'A';
13. }
14. }
15. printf("%s", st);
16. return 0;
17. }
判断题
1)输入的字符串只能由小写字母或大写字母组成。()
2)若将第8行的“i = 1”改为“i = 0”,程序运行时会发生错误。()
3)若将第8行的“i <= n”改为“i * i <= n”,程序运行结果不会改变。()
4)若输入的字符串全部由大写字母组成,那么输出的字符串就跟输入的字符串一样。()
选择题
5)若输入的字符串长度为18,那么输入的字符串跟输出的字符串相比,至多有()个字符不同。
A. 18
B. 6
C. 10
D. 1
6)若输入的字符串长度为(),那么输入的字符串跟输出的字符串相比,至多有36个字符不同。
A. 36
B. 100000
C. 1
D. 128
解析:程序意义:将是小写字母且 i是 n 的因子的元素转为大写字母。
- 错误,输入数据只要没出现溢出问题都可以
- 正确,n%0会报错
- 错误,可以带个数据进入计算,如:n=4
- 正确,大写字母不发生变化
- 18的约数有:1 2 3 6 9 18,最多6个会被转为大写。
- 问题转化:一个数 N 的因子个数为 M=36, 则 N 可能是?
由于是选择题,那么可以带入计算:如:
\(128 = 2^7,其因子个数为:\prod_{i=1}^{k}{(a_i+1)}=8.\)
\(100000 = 10^5=(2*5)^5=2^5*5^5, \prod_{i=1}^{k}{(a_i+1)}=6*6=36.\)
上面用到了约数个数定理,这里介绍一下:
对于一个大于1的正整数n可以分解质因数:\(n = \prod_{i=1}^k{p_i^{a_i}} = p_1^{a_1}*p_2^{a_2}*...*p_k^{a_k}\)
显然,对于 \(p_i^{a_i}\),它的因数为 \(p_i^{0},p_i^{1},p_i^{2},...,p_i^{a_i}\), 共 \(a_i+1\) 个
所以 n 的约数个数为:\(\prod_{i=1}^k {(a_i+1)} = (a_1+1)*(a_2+1)*...*(a_k+1)\).
第 17 题(本题共 12 分)
1. #include<cstdio>
2. using namespace std;
3. int n, m;
4. int a[100], b[100];
5.
6. int main() {
7. scanf("%d%d", &n, &m);
8. for (int i = 1; i <= n; ++i)
9. a[i] = b[i] = 0;
10. for (int i = 1; i <= m; ++i) {
11. int x, y;
12. scanf("%d%d", &x, &y);
13. if (a[x] < y && b[y] < x) {
14. if (a[x] > 0)
15. b[a[x]] = 0;
16. if (b[y] > 0)
17. a[b[y]] = 0;
18. a[x] = y;
19. b[y] = x;
20. }
21. }
22. int ans = 0;
23. for (int i = 1; i <= n; ++i) {
24. if (a[i] == 0)
25. ++ans;
26. if (b[i] == 0)
27. ++ans;
28. }
29. printf("%d", ans);
30. return 0;
31. }
假设输入的n和m都是正整数,x和y都是在[1, n]的范围内的整数,完成下面的判断题和单选题:
判断题
1)当m>0时,输出的值一定小于2n。()
2)执行完第27行的"++ans"时,ans —定是偶数。()
3)a[i]和b[i]不可能同时大于0。()
4)右程序执行到第13行时,x总是小于y,那么第15行不会被执行。()
选择题
5)若m个x两两不同,且m个y两两不同,则输出的值为()
A. 2n-2m
B. 2n+2
C. 2n-2
D. 2n
6)若m个x两两不同,且m个y都相等,则输出的值为()
A. 2n-2
B. 2n
C. 2m
D. 2n-2m
解析:没读明白程序也可以完成
1) 这里个人觉得题目的描述不严谨,没说明范围的问题,应当是默认输入数据的范围合法,保证一定不会出现下标越界情况,那么这个就是正确的,x 和 y 都是在 [1,n] 只要执行过程序中的赋值操作a[x]=y,a[y]=x 那么比如有数据被修改,为0的个数自然减少。
2) 错误, b[a[x]] = 0; a[b[y]] = 0; 其修改数值可能相同 a[x]=b[y],则不成对。
3) 错误,带个特殊值 x=y=1, a[1]=b[1]=1
4) 错误,x=1, y=2, a[x]=1, b[y]=0;
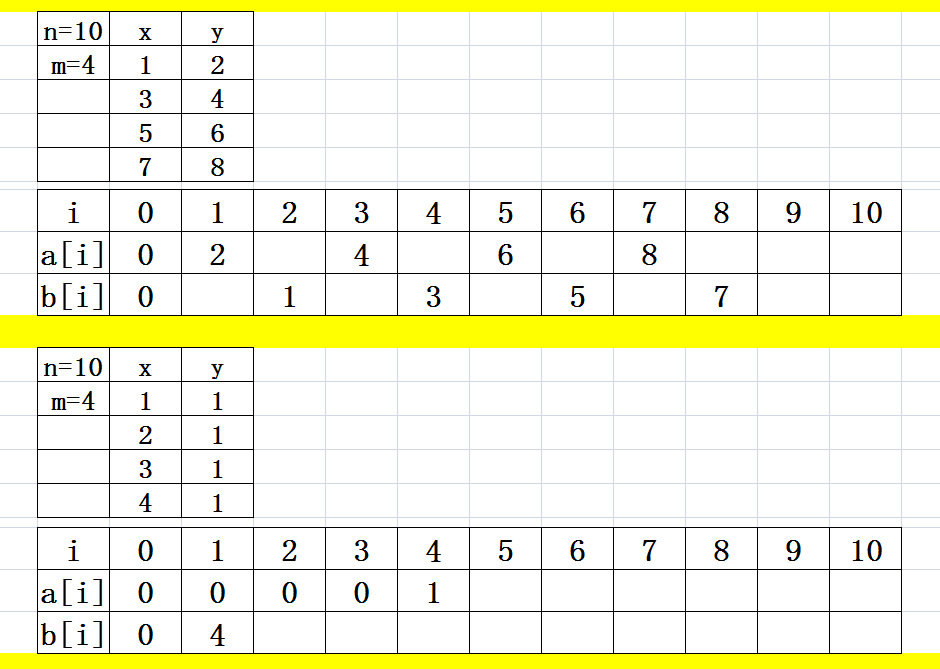
5) 2N-2M,带组数据计算即可,如下。
6) 2N-2,带组数据计算即可,如下。
第 18 题(本题共 16 分)
1. #include <iostream>
2. using namespace std;
3. const int maxn = 10000;
4. int n;
5. int a[maxn];
6. int b[maxn];
7. int f(int l, int r, int depth) {
8. if (l > r)
9. return 0;
10. int min = maxn, mink;
11. for (int i = l; i <= r; ++i) {
12. if (min > a[i]) {
13. min = a[i];
14. mink = i;
15. }
16. }
17. int lres = f(l, mink - 1, depth + 1);
18. int rres = f(mink + 1, r, depth + 1);
19. return lres + rres + depth * b[mink];
20. }
21. int main() {
22. cin >> n;
23. for (int i = 0; i < n; ++i)
24. cin >> a[i];
25. for (int i = 0; i < n; ++i)
26. cin >> b[i];
27. cout << f(0, n - 1, 1) << endl;
28. return 0;
29. }
判断题
1)如果a数组有重复的数字,则程序运行时会发生错误。()
2)如果b数组全为0,则输出为0。()
选择题
3)当n=100时,最坏情况下,与第12行的比较运算执行的次数最接近的是:()。
A. 5000
B. 600
C. 6
D. 100
4)当n=100时,最好情况下,与第12行的比较运算执行的次数最接近的是:()。
A. 100
B. 6
C. 5000
D. 600
5)当n=10时,若b数组满足,对任意0<=i<n,都有b[i] = i + 1,那么输出最大为()。
A. 386
B. 383
C. 384
D. 385
6)(4分)当n=100时,若b数组满足,对任意0 S i < 71,都有b[i]=1,那么输出最小为()。
A. 582
B. 580
C. 579
D. 581
解析:将数组b根据数组a值构造成一棵二叉树,每次在序列中选择a值最小且最靠前的元素作为根,根之前的序列构建左子树,根之后的序列构建右子树。最后求每个节点值b[i]乘深度deep的和。
当然,如果没有看懂程序也是可以做的。
1)有重复的数字但是对取最小值没有影响
2)b数组全为0,则 depth * b[mink]=0; 又 if(l>r)return 0; 所以正确
3) 最坏情况:就是一个降序序列,需要比较的次数 \(100+99+98+...+1=5050\)
4) 最好情况,就是二分,需要比较的次数 \(100log_{100}=600\)
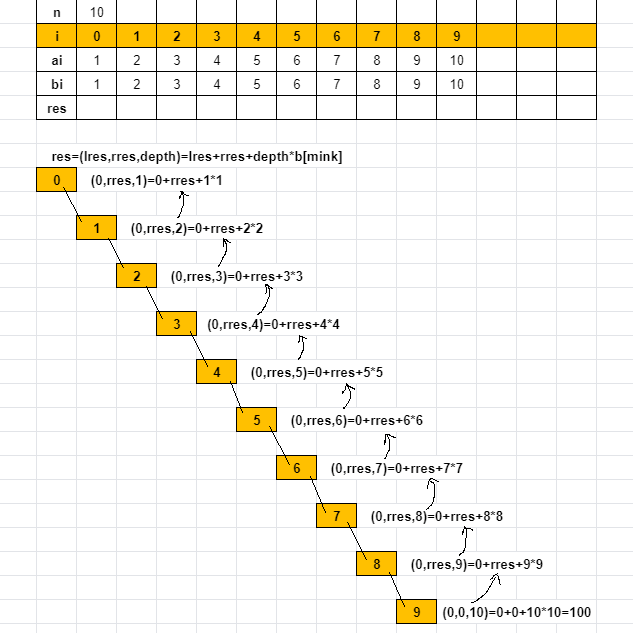
5) 代入演算得,\(1^2+2^2+3^2+...+10^2=385\),如下图
- b[i]=1, 即构造一棵100个节点的二叉树,想要节点深度和最小则尽可能弄成完全二叉树/平衡二叉树。
\(\sum depth * cnt[depth] = 1*1+2*2+3*4+4*8+5*16+6*32+7*37=580\)
三、完善程序
(单选题,每小题 3 分,共计 30 分)
第 19 题(本题共 15 分)
1、(矩阵变幻)有一个奇幻的矩阵,在不停的变幻,其变幻方式为:
数字 0 变成矩阵
0 0
0 1
数字 1 变成矩阵
1 1
1 0
最初该矩阵只有一个元素 0,变幻 n 次后,矩阵会变成什么样?
例如,矩阵最初为:[0];
矩阵变幻 1 次后:
0 0
0 1
矩阵变幻 2 次后:
0 0 0 0
0 1 0 1
0 0 1 1
0 1 1 0
输入一行一个不超过 10 的正整数 n。输出变幻 n 次后的矩阵。试补全程序。
提示:<< 表示二进制左移运算符,例如(11)2 << 2 = (1100)2
而 ^ 表示二进制异或运算符,它将两个参与运算的数中的每个对应的二进制位—进行比较,若两个二进制位相同,则运算结果的对应二进制位为 0 ,反之为 1。
1. #include <cstdio>
2. using namespace std;
3. int n;
4. const int max_size = 1 << 10;
5.
6. int res[max_size][max_size];
7.
8. void recursive(int x, int y, int n, int t) {
9. if (n == 0) {
10. res[x][y] = ①;
11. return;
12. }
13. int step = 1 << (n - 1);
14. recursive(②, n - 1, t);
15. recursive(x, y + step, n - 1, t);
16. recursive(x + step, y, n - 1, t);
17. recursive(③, n - 1, !t);
18. }
19.
20. int main() {
21. scanf("%d", &n);
22. recursive(0, 0, ④);
23. int size = ⑤;
24. for (int i = 0; i < size; i++) {
25. for (int j = 0; j < size; j++)
26. printf("%d", res[i][j]);
27. puts("");
28. }
29. return 0;
30. }
1) ①处应填()
A. n%2
B. 0
C. t
D. 1
解析: t,要给当前位置赋值为 t。
2) ②处应填()
A. x-step,y-step
B. x,y-step
C. x-step,y
D. x,y
解析: 三个t,一个 !t,可以推断出(2)是左上方矩阵,矩阵左上角坐标为(x,y)。
3) ③处应填()
A. x-step,y-step
B. x+step,y+step
C. x-step,y
D. x,y-step
解析: 三个t,一个 !t,可以推断出(3)是右下方矩阵,矩阵左上角坐标为(x+step,y+step)。
4) ④处应填()
A. n-1,n%2
B. n,0
C. n,n%2
D. n-1,0
解析:最初该矩阵只有一个元素 0,根据函数recursive的操作可以确定传入n。
5) ⑤处应填()
A. 1<<(n+1)
B. 1<<n
C. n+1
D. 1<<(n-1)
解析:矩阵宽度 size = 1<<n。
第 20 题(本题共 15 分)
2、(计数排序)计数排序是一个广泛使用的排序方法。下面的程序使用双关键字计数排序,将n对10000以内的整数,从小到大排序。例如有三对整数(3,4)、(2,4)、(3,3),那么排序之后应该是(2,4)、(3,3)、(3,4) 。
输入第一行为n,接下来 n行,第i行有两个数 a[i]和 b[i],分别表示第i对整数的第一关键字和第二关键字。
从小到大排序后输出。
数据范围 \(1<n<10^7, 1<a[i],b[i]<10^4\)
提示:应先对第二关键字排序,再对第一关键字排序。数组ord[]存储第二关键字排序的结果,数组res[]存储双关键字排序的结果。
试补全程序。
1. #include <cstdio>
2. #include <cstring>
3. using namespace std;
4. const int maxn = 10000000;
5. const int maxs = 10000;
6.
7. int n;
8. unsigned a[maxn], b[maxn],res[maxn], ord[maxn];
9. unsigned cnt[maxs + 1];
10. int main() {
11. scanf("%d", &n);
12. for (int i = 0; i < n; ++i)
13. scanf("%d%d", &a[i], &b[i]);
14. memset(cnt, 0, sizeof(cnt));
15. for (int i = 0; i < maxs; ++i)
16. ①; // 利用 cnt 数组统计数量
17. for (int i = 0; i < n; ++i)
18. cnt[i + 1] += cnt[i];
19. for (int i = 0; i < n; ++i)
20. ②; // 记录初步排序结果
21. memset(cnt, 0, sizeof(cnt));
22. for (int i = 0; i < n; ++i)
23. ③; // 利用 cnt 数组统计数量
24. for (int i = 0; i < maxs; ++i)
25. cnt[i + 1] += cnt[i];
26. for (int i = n - 1; i >= 0; --i)
27. ④ // 记录最终排序结果
28. for (int i = 0; i < n; i++)
29. printf("%d %d", ⑤);
30.
31. return 0;
32. }
1)①处应填( )
A. ++cnt[i]
B. ++cnt[b[i]]
C. ++cnt[a[i]*maxs+b[i]]
D. ++cnt[a[i]]
解析:B,先对第二关键字进行计数。
2)②处应填 ( )
A. ord[--cnt[a[i]]]=i
B, ord[--cnt[b[i]]]=a[i]
C. ord[--cnt[a[i]]]=b[i]
D. ord[--cnt[b[i]]]=i
解析:D,cnt[b[i]]表示按第二关键字排序,第i个数排第几位。ord[i]表示第i小的数在原序列的位置。
3)③处应填( )
A. ++cnt[b[i]]
B. ++cnt[a[i]*maxs+ b[i]]
C. ++cnt[a[il]
D. ++cnt[i]
解析:C。对第一关键字进行计数。
4)④处应填( )
A. res[--cnt[a[ord[i]]]]=ord[i]
B. res[--cnt[b[ord[i]]]]=ord[i]
C. res[--cnt[b[i]]]=ord[i]
D. res[--cnt[a[i]]]=ord[i]
解析:A,对第一关键字进行计数,res[i]表示第一关键字第i小的数在原序列的位置。
5)⑤处应填( )
A. a[i],b[i]
B. a[res[i]], b[res[i]]
C. a[ord[res[i]]], b[ord[res[i]]]
D. a[res[ord[i]]], b[res[ord[i]]]
解析:B,res[i]记录第i个数的在原序列的位置。且a、b数组内容必然成对输出,下标必须一致,也可以简单猜测选B。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号