SMO算法精解

　　本文参考自：https://www.zhihu.com/question/40546280/answer/88539689　　

　　解决svm首先将原始问题转化到对偶问题，而对偶问题则是一个凸二次规划问题，理论上你用任何一个解决凸二次规划的软件包都可以解决，但是这样通常来说很慢，大数据情况下尤其不实际，

　　smo是微软研究院的大神发明的解决svm对偶问题的优化算法，可以更快找到好的解。通常而言分简化版和优化版smo算法。
　　简化版:每次迭代随机选取alpha_i和alpha_j,当然其中要有一个违反kkt条件，通常先选一个违反kkt条件的alpha_i，然后随机选择一个alpha_j,然后用类似坐标上升(下降)的算法来优化目标函数，具体细节题主可以看相关代码，推荐《machine learning in action》的svm部分，但是这样的优化方式并不是最快的；
　　优化版:用启发式的算法选择alpha_j,即选择alpha_j,使得|Ei-Ej|最大，至于为什么，因为变量的更新步长正比于|Ei-Ej|,也就是说我们希望变量更新速度更快，其余的和简化版其实区别不大；
　　应该还有其他版本的smo，没看过不做评论，希望对题主有用。

　　SMO(Sequential Minimal Optimization)是针对求解SVM问题的Lagrange对偶问题，一个二次规划式，开发的高效算法。

　　传统的二次规划算法的计算开销正比于训练集的规模，而SMO基于问题本身的特性（KKT条件约束）对这个特殊的二次规划问题的求解过程进行优化。

　　对偶问题中我们最后求解的变量只有Lagrange乘子向量，这个算法的基本思想就是每次都只选取一对，固定向量其他维度的元素的值，然后进行优化，直至收敛。

　　SMO干了什么？
　　首先，整个对偶问题的二次规划表达如下：
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　　SMO在整个二次规划的过程中也没干别的，总共干了两件事：

• 选取一对参数
• 固定向量的其他参数，将代入上述表达式进行求最优解获得更新后的

　　SMO不断执行这两个步骤直至收敛。

　　因为有约束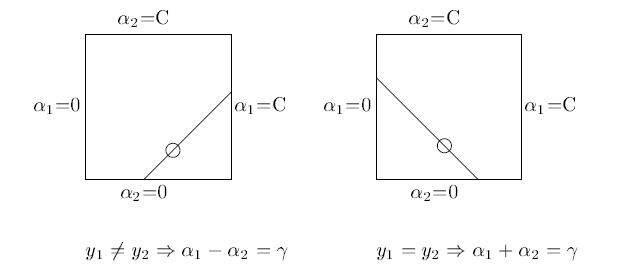存在，实际上和的关系也可以确定。这两个参数的和或者差是一个常数。

　　所以虽然宣传上说是选择了一对，但还是选择了其中一个，将另一个写作关于它的表达式代入目标函数求解。

　　为什么SMO跑的那么快，比提出之前的算法不知道高到哪里去了？
　　正如上面提到的，在固定其他参数以后，这就是一个单变量二次规划问题，仅有的约束也是这个变量，显然有闭式解。不必再调用数值优化算法。

　　KKT条件是对偶问题最优解的必要条件：
　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　除了第一个非负约束以外，其他约束都是根据目标函数推导得到的最优解必须满足的条件，如果违背了这些条件，那得到的解必然不是最优的，目标函数的值会减小。

　　所以在SMO迭代的两个步骤中，只要中有一个违背了KKT条件，这一轮迭代完成后，目标函数的值必然会增大。Generally speaking，KKT条件违背的程度越大，迭代后的优化效果越明显，增幅越大。

　　怎样跑的更快？
　　和梯度下降类似，我们要找到使之优化程度最大的方向（变量）进行优化。所以SMO先选取违背KKT条件程度最大的变量，那么第二个变量应该选择使目标函数值增大最快的变量，但是这个变量怎么找呢？比较各变量优化后对应的目标函数值的变化幅度？这个样子是不行的，复杂度太高了。

　　SMO使用了一个启发式的方法，当确定了第一个变量后，选择使两个变量对应样本之间最大的变量作为第二个变量。直观来说，更新两个差别很大的变量，比起相似的变量，会带给目标函数更大的变化。间隔的定义也可以借用偏差函数
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　　我们要找的也就是使对于来说使最大的

　　很惭愧，只做了一点微小的工作。

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

SVM算法优点：

(1)非线性映射是SVM方法的理论基础,SVM利用内积核函数代替向高维空间的非线性映射；

(2)对特征空间划分的最优超平面是SVM的目标,最大化分类边际的思想是SVM方法的核心；

(3)支持向量是SVM的训练结果,在SVM分类决策中起决定性作用。因此，模型需要存储空间小，算法鲁棒性（ Robust ）强。

SVM算法缺点：

(1) SVM算法对大规模训练样本难以实施

由于SVM是借助二次规划来求解支持向量，而求解二次规划将涉及m阶矩阵的计算（m为样本的个数），当m数目很大时该矩阵的存储和计算将耗费大量的机器内存和运算时间。

(2) 用SVM解决多分类问题存在困难

经典的支持向量机算法只给出了二类分类的算法，而在数据挖掘的实际应用中，一般要解决多类的分类问题。 

基于以上问题，我们现在讨论SOM（ Sequential Minimal Optimization algorithm ）算法。

 

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

1、SMO算法的原理

　　这一被称为“顺次最小优化”的算法和以往的一些SVM改进算法一样，是把整个二次规划问题分解为很多易于处理的小问题，所不同的是，只有SMO算法把问题分解到可能达到的最小规模：每次优化只处理两个样本的优化问题，并且用解析的方法进行处理。我们将会看到，这种与众不同的方法带来了一系列不可比拟的优势。

　　对SVM来说，一次至少要同时对两个样本进行优化（就是优化它们对应的Lagrange乘子），这是因为等式约束的存在使得我们不可能单独优化一个变量。

　　所谓“最小优化”的最大好处就是使得我们可以用解析的方法求解每一个最小规模的优化问题，从而完全避免了迭代算法。

　　当然，这样一次“最小优化”不可能保证其结果就是所优化的Lagrange乘子的最终结果，但会使目标函数向极小值迈进一步。我们再对其它Lagrange乘子做最小优化，直到所有乘子都符合KKT条件时，目标函数达到最小，算法结束。

　　这样，SMO算法要解决两个问题：一是怎样解决两个变量的优化问题，二是怎样决定先对哪些Lagrange乘子进行优化。

2、SMO算法的特点和优势 
　　SMO算法和以往流行的SVM优化算法如块算法、固定工作样本集法相比，既有共同点，又有自己的独特之处。

　　共同点在于它们都是把一个大的优化问题分解为很多小问题来处理。块算法在每一步中将新加入样本中违反KKT条件的样本与原有的支持向量一起组成小问题的样本集进行优化，优化完毕后只保留其中的支持向量，再加进来新的样本进入下一步。固定工作样本集法是每一步只收集新加入样本中“最坏”的样本，并将原来保留的支持向量集中“较好”的替换出去，以保持样本集大小不变。SMO则是把每一步的优化问题缩减到了最小，它可以看作是固定工作样本集法的一种特殊情况：把工作样本集的大小固定为2，并且每一步用两个新的Lagrange乘子替换原有的全部乘子。

　　SMO的最大特色在于它可以采用解析的方法而完全避免了二次规划数值解法的复杂迭代过程。这不但大大节省了计算时间，而且不会牵涉到迭代法造成的误差积累（其它一些算法中这种误差积累带来了很大的麻烦）。理论上SMO的每一步最小优化都不会造成任何误差积累，而如果用双精度数计算，舍入误差几乎可以忽略，于是所有的误差只在于最后一遍检验时以多大的公差要求所有Lagrange乘子满足KKT条件。可以说SMO算法在速度和精度两方面都得到了保证。

　　SMO在内存的节省上也颇具特色。我们看到，由于SMO不涉及二次规划数值解法，就不必将核函数矩阵整个存在内存里，而数值解法每步迭代都要拿这个矩阵作运算。（4000个样本的核函数矩阵需要128M内存！）于是SMO使用的内存是与样本集大小成线性增长的，而不象以往的算法那样成平方增长。在我们的程序中SMO算法最多占用十几兆内存。SMO使得存储空间问题不再是SVM应用中的另一个瓶颈。

　　SMO算法对线性支持向量机最为有效，对非线性则不能发挥出全部优势，这是因为线性情况下每次最小优化后的重置工作都是很简单的运算，而非线性时有一步加权求和，占用了主要的时间。其他算法对线性和非线性区别不大，因为凡是涉及二次规划数值解的算法都把大量时间花在求数值解的运算中了。

　　当大多数Lagrange乘子都在边界上时，SMO算法的效果会更好。 
　　尽管SMO的计算时间仍比训练集大小增长快得多，但比起其它方法来还是增长得慢一个等级。因此SMO较适合大数量的样本。