扑克游戏【堆】
题目大意:

3
5 10 13
43思路:
1.贪心
贪心的过程有点乱。为了让答案平均,我将所有的牌放在树的相邻两层之间,起到平均的作用。将大数放在上,小数放在下,求最小值。
但是这样是错误的。
比如说这组数据:
4
10 1 1 1正确答案:
18贪心答案:
26(当然我们年级WYC大佬用贪心过了这个样例,但是究竟还是WA了)
代码被吃了。
思路二:DFS
可以用求出每一种可能方案,再在其中求出最小值。
这样做最然不会WA,但是有个叫做TLE的东西会跑出来烦你。
代码还没被吃:
额,那个数组有点难解释,反正不对,就不解释了。
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int p=17;
const int inf=999999999;
int a[100001],n,m,ans,t,o[21],sum;
void dfs(int x,int k)
{
if (!x) //搜索完了
{
if (ans>k) ans=k;
return;
}
for (int i=1;i<=t;i++)
{
if (k+i*a[x]>=ans) break; //(没用的)剪枝
if (sum>=o[i])
{
sum-=o[i];
dfs(x-1,k+i*a[x]); //往下搜
sum+=o[i];
}
}
return;
}
void csh() //初始化o数组
{
o[p]=1;
for (int i=p-1;i>=1;i--)
o[i]=o[i+1]*2;
sum=2*o[1];
ans=inf;
}
void init()
{
scanf("%d",&n);
t=(int)log2((double)n-0.0000001)+2;
for (int i=1;i<=n;i++)
scanf("%d",&a[i]);
sort(a+1,a+1+n);
}
int main()
{
csh();
init();
dfs(n,0);
printf("%d\n",ans);
return 0;
}正解:合并果子!
不信?把你合并果子AC代码交这一道题试一下?输入输出都不用改!
思路三:堆
合并果子的原理相信大家都知道了,在这里解释一下为是么这道题会是合并果子。
对于一棵树(样例)
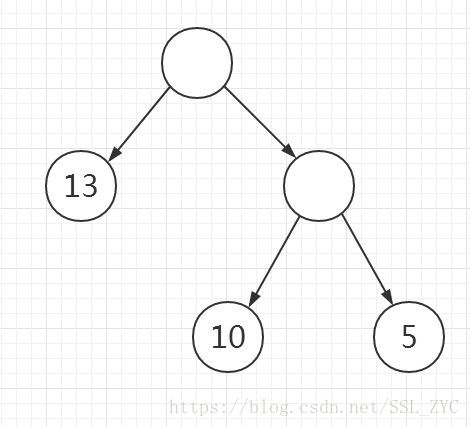
我们用合并果子的方法将它根节点求出。
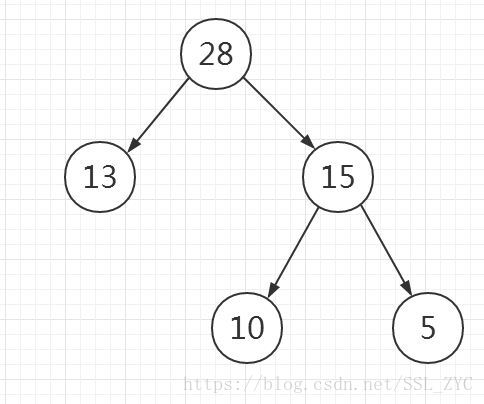
那么这时的答案是 28+15=43,正是正确答案。
那么为什么会是正确答案呢?
我们将43分解一下。
43=28+15
=(13+15)+(10+5)
=(13+(10+5))+(10+5)
=13+10+5+10+5
=131+102+52
再回到题目给出的图案上
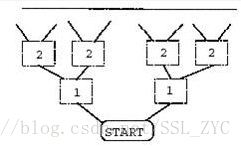
就会发现,13,10,5所乘的数字正好是它在树的层数!(题目说了根节点为0层)
所以,这道题与合并果子完全一样!
代码:
//与合并果子完全一样,就不解释了
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;
const int inf=99999999;
int n,a[10001],x,y,sum,m,p,d;
void up(int x)
{
while(x>1&&a[x]<a[x/2])
{
swap(a[x],a[x/2]);
x/=2;
}
}
void down(int x)
{
int y=x*2;
while ((y<=n&&a[y]<a[x])||(y+1<=n&&a[y+1]<=a[x]))
{
if (a[y]>a[y+1]) y++;
swap(a[y],a[x]);
x=y;
y=x*2;
}
}
int main()
{
scanf("%d",&n);
for (int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
up(i);
}
while(n>1)
{
d=a[1];
a[1]=a[n];
n--;
down(1);
d+=a[1];
a[1]=a[n];
n--;
down(1);
n++;
a[n]=d;
sum+=d;
up(n);
}
printf("%d\n",sum);
return 0;
}