七夕祭【模拟】

题目大意：

有一个会场由N$N$排M$M$列共计N×M$N\times M$个摊点组成。但是小L$L$只对其中的一部分摊点感兴趣。他预先联系了会场的负责人，希望能够通过恰当地布置会场，使得各行中他感兴趣的摊点数一样多，并且各列中他感兴趣的摊点数也一样多。
但是摊点已经随意布置完毕了，如果想满足小L$L$的要求，唯一的调整方式就是交换两个相邻的摊点。两个摊点相邻，当且仅当他们处在同一行或者同一列的相邻位置上，每一行或每一列的第一个位置和最后一个位置也算作相邻。现在小L$L$想知道他的两个要求最多能满足多少个。在此前提下，至少需要交换多少次摊点。
Input$Input$

2 3 4
1 3
2 1
2 2
2 3

Output$Output$

row 1

---

思路：

如果这道题只有一行，且一行的最后和第一不相连的话，就很容易想到 均分纸牌 。所以说，这道题其实就是均分纸牌的进阶版。
但是这道题并不能贪心。毕竟O(N2)$O(N^2)$还是吃不消的。
如果使用均分纸牌的方法，那么就枚举从第k$k$个位置开始，像均分纸牌的方法一样依次向后推。最后取最小值。预计得分 70 分。

#include <cstdio>
using namespace std;
int n,a[101],mid,sum,x;

int main()
{
    scanf("%d",&n);
    for (int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        mid+=a[i];  //求n个数的总和 
    } 
    mid/=n;  //算平均值 
    for (int i=1;i<=n;i++)
    {
        if (a[i]!=mid)  //如果a[i]不等于mid 
        {
            sum++;  //移动次数加1 
            x=a[i]-mid;  //假设a[i]比mid大x（x可以为负数） 
            a[i+1]+=x; 
        }
    }
    printf("%d\n",sum);
    return 0;
}

其实洛谷上还有另外一道题很像这道题。糖果传递，跟这道题就真的很像了。
可以利用前缀和的思想，求出每一行的感兴趣摊点的个数，将这些前缀和排序，再求出中位数，按照|s1−sk|+|s2−sk|+|s3−sk|+……+|sn−sk|$|s1-sk|+|s2-sk|+|s3-sk|+\dots \dots +|sn-sk|$公式求出答案即可。
那么为什么选择中位数就一定对呢？
我们把这个问题看成一条路上有m$m$户人家，要在这条路上打一口井，问选择哪里打井可以使所有人家到达井的总路程最小？

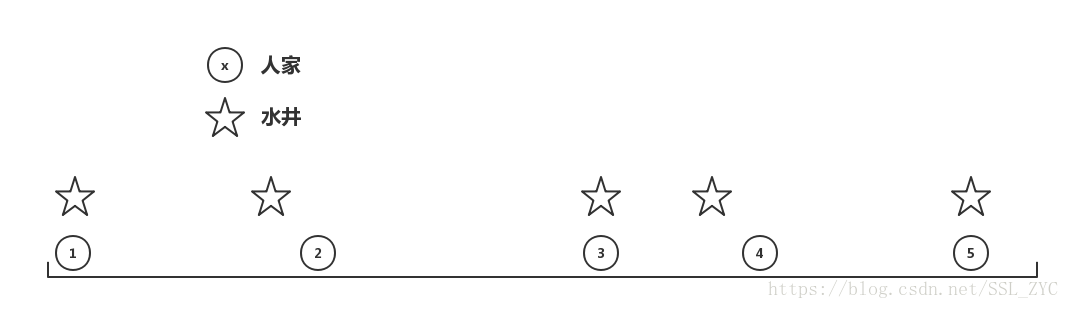
不难发现，水井有无限个位置可以放，但是肯定是放2$2$号人加到4$4$号人家之间最优。那么在那个点是在最优中最优呢？

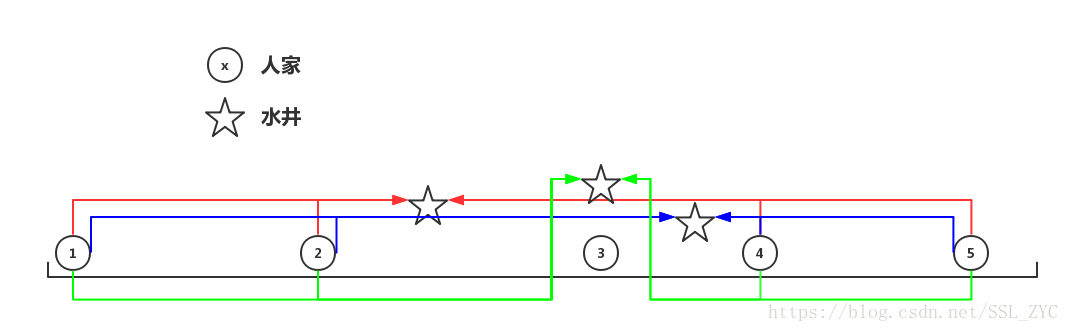
无论水井放在2$2$号人家和4$4$号人家之间的那个点，除3$3$号人家外的所有点到达水井的距离都是不变的。那么问题就转化成了：水井放在哪里距离3号人家最近？
那这个问题就很明显了：放在3$3$号人家的门口肯定离3$3$号人家最近嘛！
所以说，无论有3,5,7...2x+1$3,5,\mathrm{7...2}x+1$个人家，只要放在最中间（中位数）的人家就一定满足最优。
那么当人家为偶数个呢？


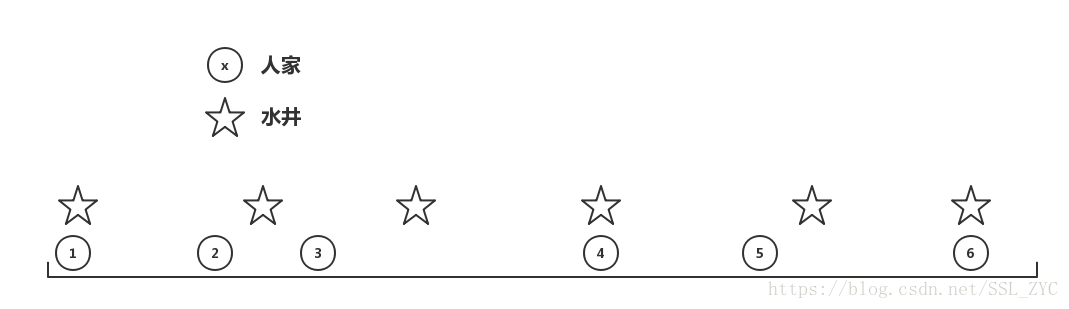
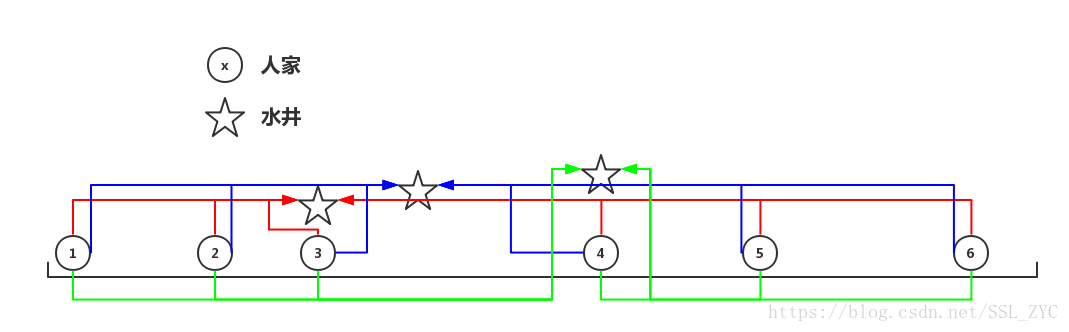
那么，只要水井放在中间两户人家（3$3$号人家和4$4$号人家）之间，答案都最优。
所以，如果这道题选择中位数，那么一定能保证答案最优。

---

代码：

#include <cstdio>
#include <algorithm>
#include <iostream>
using namespace std;

long long h[100001],l[100001],x,y,n,m,k,sum,s1[100001],s2[100001],z1,z2;

void H()  //计算行
{
    for (int i=1;i<=n;i++)
     s1[i]=s1[i-1]+h[i]-z1;  //前缀和
    sort(s1+1,s1+1+n);  //排序
    int mid=s1[(n+1)/2];  //中位数
    for (int i=1;i<=n;i++)
     sum+=abs(s1[i]-mid);  //公式
}

void L()  //计算列
{
    for (int i=1;i<=m;i++)
     s2[i]=s2[i-1]+l[i]-z2;
    sort(s2+1,s2+1+m);
    int mid=s2[(m+1)/2];
    for (int i=1;i<=m;i++)
     sum+=abs(s2[i]-mid);
}

int main()
{
    scanf("%lld%lld%lld",&n,&m,&k);
    z1=k/n;
    z2=k/m;
    for (int i=1;i<=k;i++)
    {
        scanf("%lld%lld",&x,&y);
        h[x]++;
        l[y]++;
    }
    if ((!(k%n))&&(!(k%m)))  //both情况
    {
        printf("both ");
        H();
        L();
    }
    else if (!(k%n))  //row情况
    {
        printf("row ");
        H();
    }
    else if (!(k%m))  //column情况
    {
        printf("column ");
        L();
    }
    else return printf("impossible")&0;
    return printf("%lld\n",sum)&0;
}