【模板】线段树1【线段树】

题目大意：

已知一个数列，你需要进行下面两种操作：

1. 将某区间每一个数加上x
2. 求出某区间每一个数的和

Input$Input$

5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

Output$Output$

11
8
20

---

思路：

这还用说吗肯定是线段树啊！

上代码：
思路都没讲上啥代码。
这道题是一道很模板的线段树，暴力或前缀和都只能拿70分。
线段树是啥啊？
emm，其实基本上就是一棵树，不过每个节点一般代表一个区间，而不是一个点。


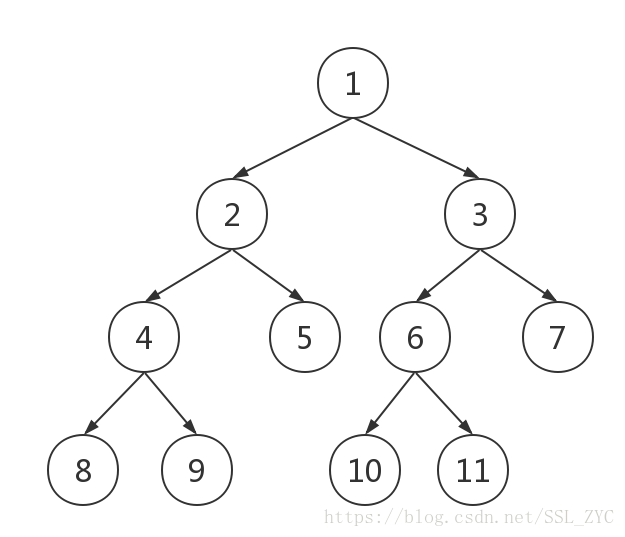
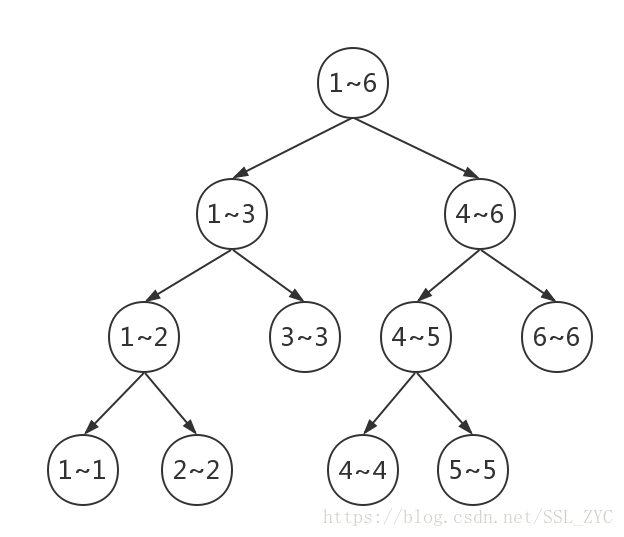
线段树能保证我们在O(logn)$O(logn)$的时间内完成单点修改或区间修改，也可以在O(logn)$O(logn)$的时间内完成单点查询或区间查询，比枚举一边O(n)$O(n)$快多了。比如说有1×109$1\times {10}^9$个数，枚举需要查询109${10}^9$次，而线段树只要30$30$次就可以！
那么如果我们要在[2,4)$[2,4)$这个区间插入数字3，那么可以这样做：





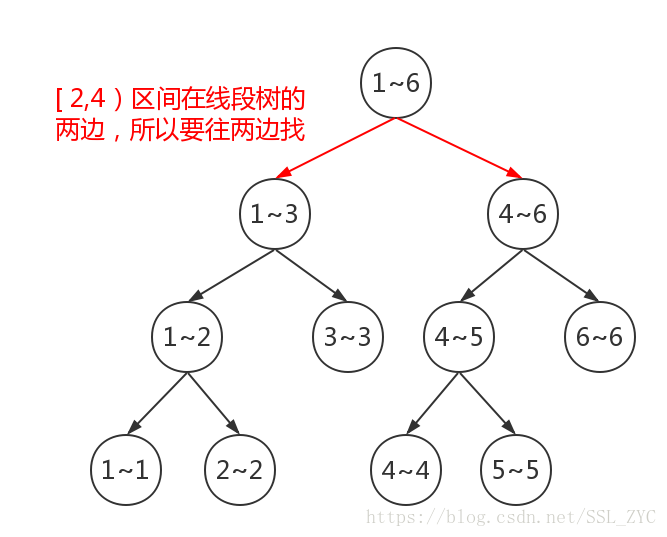
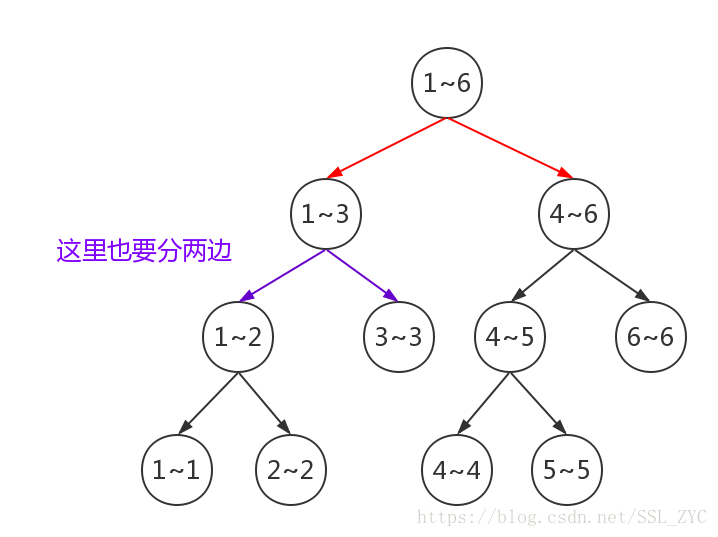
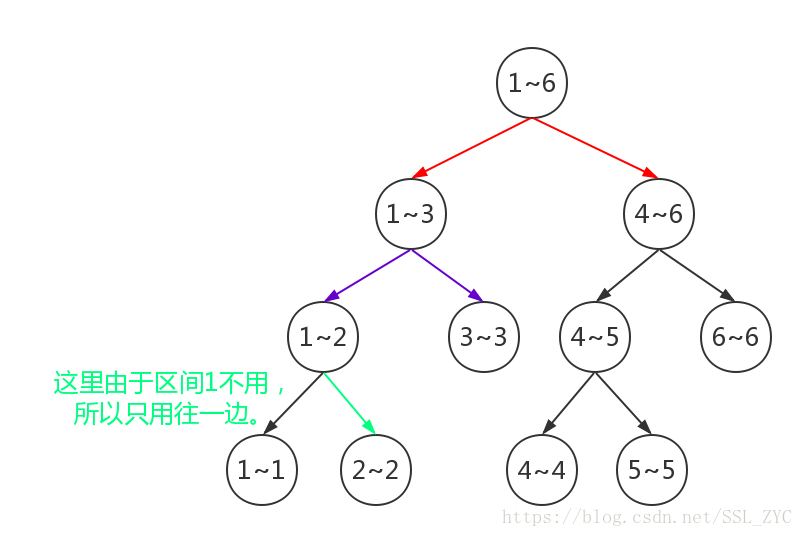
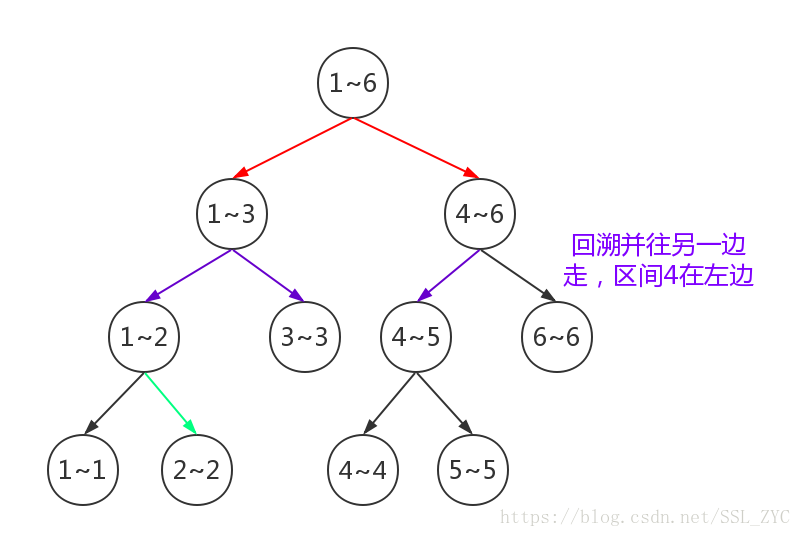
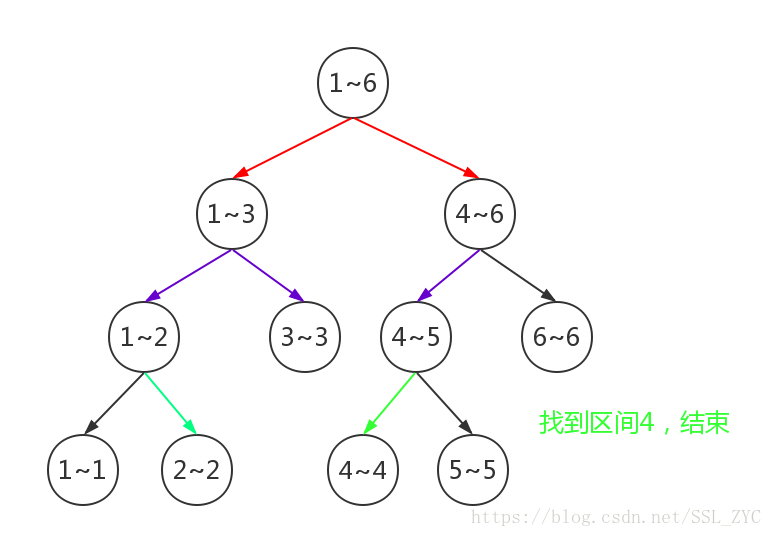
于是区间[ 2,4）就找到，并更改值了。
查询的方法与修改基本一样，在这就不多讲了。
当然，如果只要单点修改的话，树状数组是一个更好的选择。洛谷也有两道树状数组模板题

• https://www.luogu.org/problemnew/show/P3374
• https://www.luogu.org/problemnew/show/P3368

---

代码：

#include <iostream>
#include <cstdio>
using namespace std;

long long n,m,t,x,y,z,num[700001];

struct node  //结构体
{
    long long l,r,lazy,num;
}tree[2000001];

void make(long long x)  //建树
{
    if (tree[x].r<=tree[x].l) return;  //到达叶子节点
    long long mid=(tree[x].l+tree[x].r)/2;
    tree[x*2].l=tree[x].l;
    tree[x*2].r=mid;
    tree[x*2+1].l=mid+1;
    tree[x*2+1].r=tree[x].r;  //给儿子节点赋值
    make(x*2);
    make(x*2+1);  //继续建树
    return;
}

long long lazy(long long x) 
{
    return tree[x].lazy*(tree[x].r-tree[x].l+1);
}

void pushdown(long long x)  //lazy标记专属座位
{
    if (tree[x].lazy)
    {
        tree[x*2].lazy+=tree[x].lazy;
        tree[x*2+1].lazy+=tree[x].lazy;
        tree[x].num+=lazy(x);
        tree[x].lazy=0;
    }
    return;
}

void makes(long long x,long long l,long long r,long long k)  //区间修改
{
    if (l==tree[x].l&&r==tree[x].r)
    {
        tree[x].lazy+=k;
        return;
    }
    if (tree[x].r<=tree[x].l) return;
    pushdown(x);  //下传懒惰标记
    long long mid=(tree[x].l+tree[x].r)/2;
    if (r<=mid)  //完全在左边
    {
        makes(x*2,l,r,k);
        tree[x].num=tree[x*2].num+tree[x*2+1].num+lazy(x*2)+lazy(x*2+1);
        return;
    }
    if (l>mid)  //完全在右边
    {
        makes(x*2+1,l,r,k);
        tree[x].num=tree[x*2].num+tree[x*2+1].num+lazy(x*2)+lazy(x*2+1);
        return;
    }
    makes(x*2,l,mid,k);
    makes(x*2+1,mid+1,r,k);  //左右都有
    tree[x].num=tree[x*2].num+tree[x*2+1].num+lazy(x*2)+lazy(x*2+1);
    return;
}

long long find(long long x,long long l,long long r)  //区间查询
{
    if (tree[x].l==l&&tree[x].r==r)  //找到
     return lazy(x)+tree[x].num;  
    if (tree[x].r<=tree[x].l) return 0;
    long long mid=(tree[x].l+tree[x].r)/2;
    pushdown(x); 
    if (r<=mid) return find(x*2,l,r);
    if (l>mid) return find(x*2+1,l,r);  
    return find(x*2,l,mid)+find(x*2+1,mid+1,r);
}

int main()
{
    scanf("%lld%lld",&n,&m);
    tree[1].l=1;
    tree[1].r=n;
    make(1);  //建树
    for (int i=1;i<=n;i++)
    {
        scanf("%lld",&num[i]);
        num[i]+=num[i-1];  //前缀和
    } 
    while (m--)
    {
        scanf("%lld",&t);
        if (t==1)  //修改
        {
            scanf("%lld%lld",&x,&z);
            makes(1,x,x,z);
        }
        else  //查询
        {
            scanf("%lld%lld",&x,&y);
            printf("%lld\n",find(1,x,y)+num[y]-num[x-1]);
        }
    }
    return 0;
}