【JZOJ2938】分割田地【DP】
题目大意:
题目链接:https://jzoj.net/senior/#main/show/2938
题目图片:
http://wx2.sinaimg.cn/mw690/0060lm7Tly1fwecwhe8txj30j10dv74k.jpg
http://wx1.sinaimg.cn/mw690/0060lm7Tly1fwecwhdzjnj30j50dzjrf.jpg
给出的矩阵,求有多少种方案可以把这个矩阵分割成块。
思路:
很明显是啊。
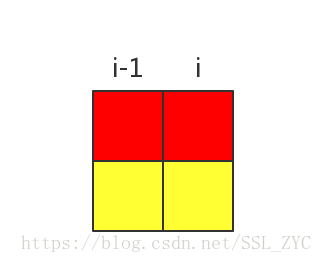
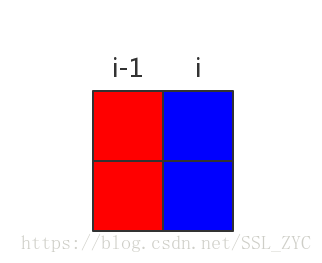
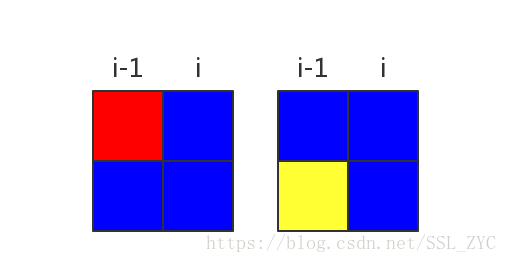
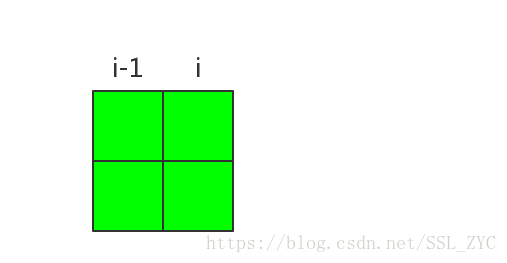
设表示选到第列,有个联通块,这一列的两个格子是否分在同一块(0表示不是,1表示是)的方案数。
那么我们分情况来看。
第列不同块,比第列多出两个块,所以
然后将这几个方程和在一起就可以了。
代码:
#include <cstdio>
#define N 1100
#define MOD 100000007
using namespace std;
int f[N][N*2][2],n,m;
void plus(int &x,int y)
{
x=(x%MOD+y%MOD)%MOD;
}
int main()
{
scanf("%d%d",&n,&m);
f[1][1][1]=1;
f[1][2][0]=1;
for (int i=2;i<=n;i++)
for (int j=1;j<=m;j++)
{
if (j>2) plus(f[i][j][0],f[i-1][j-2][0]);
if (j>2) plus(f[i][j][0],f[i-1][j-2][1]);
if (j>1) plus(f[i][j][0],f[i-1][j-1][1]*2);
if (j>1) plus(f[i][j][0],f[i-1][j-1][0]*2);
plus(f[i][j][0],f[i-1][j][0]);
if (j>2) plus(f[i][j][1],f[i-1][j-1][0]);
if (j>1) plus(f[i][j][1],f[i-1][j-1][1]);
if (j>1) plus(f[i][j][1],f[i-1][j][0]*2);
plus(f[i][j][1],f[i-1][j][1]);
}
printf("%d\n",(f[n][m][0]+f[n][m][1])%MOD);
return 0;
}







 浙公网安备 33010602011771号
浙公网安备 33010602011771号