【洛谷P1939】【模板】矩阵加速(数列)
题目大意:
题目链接:https://www.luogu.org/problemnew/show/P1939
设。求。
前言
这篇博客并不是专门来介绍矩阵乘法加速递推的。
但是既然是模板题就提一下吧。
什么是矩阵乘法?
下面是来自度娘的解释:


也就是说,对于两个矩阵和,在满足第一个矩阵的列数=第二个矩阵的行数时,这两个矩阵就可以相乘。那么假设是的矩阵,是的矩阵,那么他们相乘得到的矩阵就是一个的矩阵。
而且对于矩阵的任意元素,都等于矩阵A第i行的所有数字分别乘上矩阵B第j列的所有数字之和。(其实就是上图的公式)
矩阵乘法和递推的关系?
矩阵乘法和递推关系最密切的例子就是斐波那契数列了。↓
现在看不懂没关系,可以慢慢理解。
我们知道,斐波那契数列有这样的定义:
那么如果我们有一个的矩阵,其中第一行分别是和。我们的目标是把第一行承上一个矩阵变成和。那么应该怎么办呢?
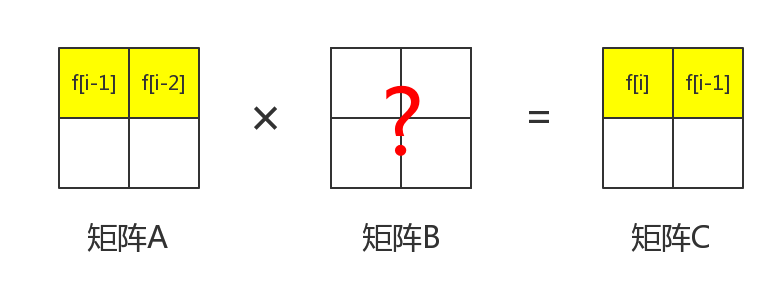
首先,矩阵和矩阵都含有这一项。那么就先从这里下手。
我们知道,矩阵的在第行第列。那么,根据公式,可以得到
也就是说
那么很明显,我们可以得到。这样可以保证进行矩阵乘法之后是。
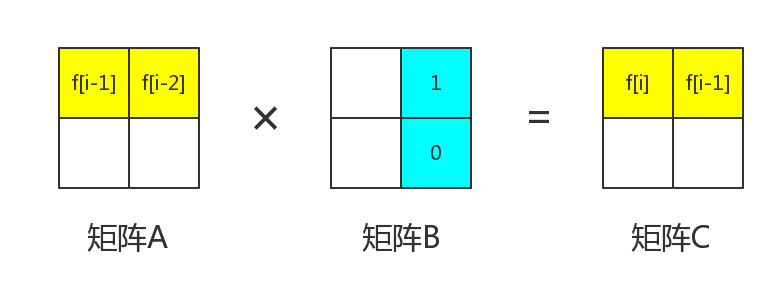
那么现在来看矩阵中的。我们要保证的是
也就是说
我们知道,。所以可以得到
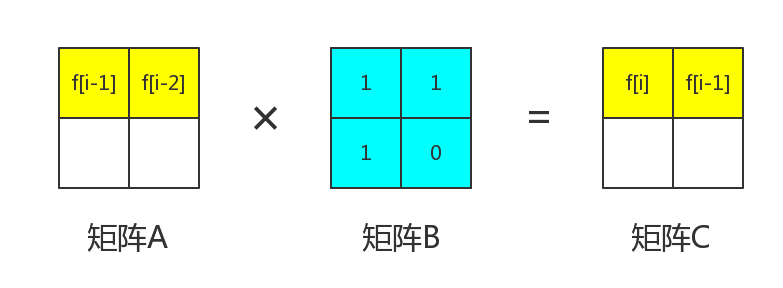
那么整个矩阵都被我们求出来了。
得到了和后,我们再将它乘一次矩阵,就可以得到和,又可以得到和
这样就可以得到了。
但是!
你以为就结束了?
这样的时间复杂度是,其中表示求斐波那契数列的第项,表示矩阵的长宽。还不如递推。而且递推可以得到到的所有斐波那契数,而矩阵乘法只能求第项。
其实还有个地方可以优化。
我们求的时候其实是将原矩阵乘了次矩阵的。也就是说
看到次方想到了什么?
可以用快速幂!
我们用快速幂的思想求出,然后再乘上一个矩阵即可。
怎么用快速幂?
其实是一个道理。只不过把矩阵乘矩阵换成矩阵乘矩阵就可以了。
那么最终的时间复杂度为。还是很优秀的。
下面进入正题。
思路:
可以发现矩阵
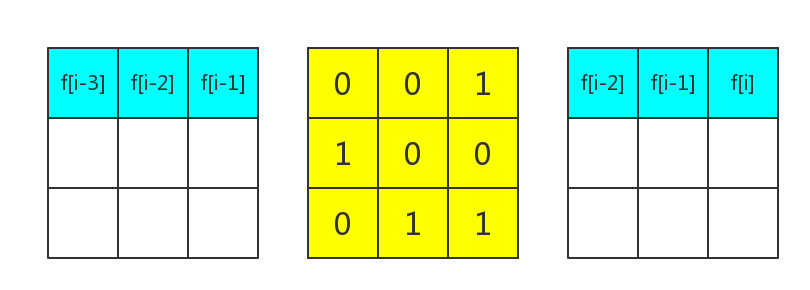
然后就是套模板了。。。
代码:
#include <cstdio>
#include <cstring>
#define MOD 1000000007
#define ll long long
using namespace std;
const ll b[4][4]=
{
{0,0,0,0},
{0,0,0,1},
{0,1,0,0},
{0,0,1,1}
};
int T,n;
ll f[4],a[4][4];
void mul(ll f[4],ll a[4][4])
{
ll c[4];
memset(c,0,sizeof(c));
for (int i=1;i<=3;i++)
for (int j=1;j<=3;j++)
c[i]=(c[i]+f[j]*a[j][i])%MOD;
memcpy(f,c,sizeof(c));
}
void mulself(ll a[4][4])
{
ll c[4][4];
memset(c,0,sizeof(c));
for (int i=1;i<=3;i++)
for (int j=1;j<=3;j++)
for (int k=1;k<=3;k++)
c[i][j]=(c[i][j]+a[i][k]*a[k][j])%MOD;
memcpy(a,c,sizeof(c));
}
void ask(int x)
{
while (x)
{
if (x&1) mul(f,a);
x>>=1;
mulself(a);
}
}
int main()
{
scanf("%d",&T);
while (T--)
{
scanf("%d",&n);
if (n<4)
{
printf("1\n");
continue;
}
memcpy(a,b,sizeof(b));
f[1]=f[2]=f[3]=1;
ask(n-3);
printf("%lld\n",f[3]);
}
return 0;
}


