【JZOJ3084】超级变变变【模拟】【规律】

题目大意：

题目链接：https://jzoj.net/senior/#main/show/3084
求在$L\sim R$中，有多少个数字经过若干次变化会转变为$k$。这个变化方式如下：

---

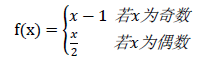
思路：

这种题目大部分都是有规律的。所以可以先打一个搜索求出$1\sim 200$中能变化成$k$的表。
然后就能发现规律如下：

• 对于任意一个偶数$k$，若一个数$x$满足在$k\times 2^y+t(y=0\sim Inf,t=0\sim2^{2y})$
  ，则$x$能经过变换得到$k$。
• 对于任意一个奇数$k$，若一个数$x$满足在$k\times 2^y+t(y=0\sim Inf,t=0\sim2^y)$，则$x$能经过变换得到$k$。

所以就用模拟求出答案即可。
时间复杂度$O(log\ B)$。

---

代码：

#include <cstdio>
#include <iostream>
using namespace std;
typedef long long ll;

ll l,r,ans,k,num=1;

int main()
{
	cin>>k>>l>>r;
	if (r<k) return !printf("0\n");
	if (!k) return !printf("%d\n",r-l+1);  //特判
	if (k&1)
	{
		while (k*num+num-1<l) num*=2;
		if (k*num>r) return !printf("0\n");
		if (k*num>=l) ans+=num;
			else ans+=k*num+num-l;
		num*=2;
		while (k*num+num-1<=r)
		{
			ans+=num;
			num*=2;
		}
		if (k*num<=r) ans+=r-k*num+1;
	}
	else
	{
		if (k+1>=l&&k+1<=r) ans++;
		while (k*num+num*2-1<l) num*=2;
		if (k*num>r) return !printf("0\n");
		if (k*num>=l) ans+=num*2;
			else ans+=k*num+num*2-l;
		num*=2;
		while (k*num+num*2-1<=r)
		{
			ans+=num*2;
			num*=2;
		}
		if (k*num<=r) ans+=r-k*num+1;
	}
	cout<<ans;
	return 0;
}